BP神經網絡在信號發生器中的應用

徐明哲

（中國電子科技集團公司第四十一研究所 山東 青島 266555）

0 引言

模擬信號源中關鍵部件壓控振蕩器的輸出頻率與調諧電壓之間是非線性關系，通常都是使用線性關系來簡單的表示兩者之間的關系，只要知道某兩個頻點的調諧電壓，根據兩點一線原理，就可以確定該線性關系，根據此線性關系，其它頻率點的調諧電壓就可以通過該線性關系找出，事實上，振蕩器輸出頻率與控制電壓并非嚴格的遵循線性關系，而是非線性的，如圖1所示：

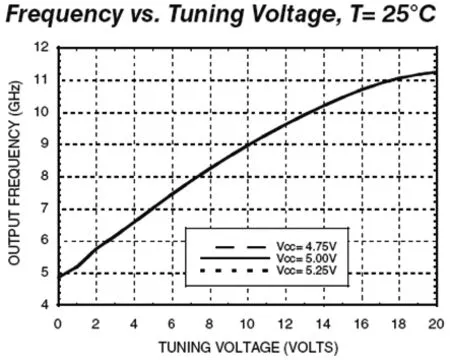
圖1 輸出頻率與調諧電壓關系圖

從圖中可以直觀的看出，在振蕩器輸出頻率的低端和高端非線性很明顯，因此若根據線性函數得到的調諧電壓v0加到振蕩器上，并不一定會輸出目標頻率f0，而是fn，并且，f0與fn之間的差值可能非常大，使控制振蕩器的鎖相環路從fn鎖定輸出到f0的時間非常長，從而影響了儀器的性能，鑒于此，本文提出了一種基于BP神經網絡的方法來擬合壓控振蕩器輸出頻率與控制電壓關系的函數fbp（v），使得f0與fn更接近以致相等，將此關系取代線性關系應用到振蕩器的調諧電壓設置上將會縮短控制環路的鎖相時間，提高儀器性能。

1 模擬合成信號源簡介

信號發生器的信號產生方式主要有兩種：模擬合成和直接數字合成。模擬合成信號源主要是依靠最核心的壓控振蕩器振蕩器來產生信號，并通過外圍控制電路來滿足信號的指標要求，如為滿足信號的功率指標，可以加功率電平控制電路，為滿足信號的頻率調制指標，可以以反饋環路的方式加頻率控制電路，如用小數環外加其它環路來控制頻率精度，為降低噪聲加本振環路等，最終的目的就是得到精準的調諧電壓來控制振蕩器，使之鎖定在要求輸出的頻率的工作狀態[1]，模擬信號源工作原理如圖2所示。

圖2 模擬合成信號源原理示意圖

如圖所示，當預置電壓很準確的時候，輸出頻率將會很快鎖定。模擬信號源認為，YIG振蕩器的輸出頻率與加在YIG振蕩器上的電壓成線性關系，該線性關系如公式（1）所示。

其中f（v）是調諧電壓為 時的輸出頻率；

a為斜率；

b為截距；

根據兩點一線原理， 只要有兩個樣點A （v1，f（v1））,B（v2，f（v2））就可以確定該公式的 a 和 b，如下所示：

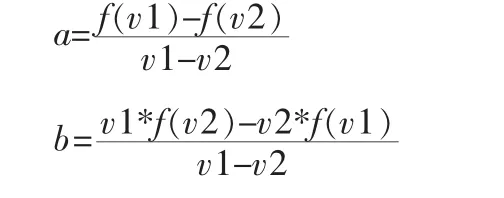
根據經驗，兩個樣點一般選取振蕩器頻率輸出范圍的三分之一和三分之二處，當要輸出目標頻率fm時，根據公式1，可以得出求控制電壓vm的公式

所以，模擬合成源一般只校準兩個頻點的預置電壓值，根據公式2就可以確定整個頻率范圍的預置電壓。

事實上，振蕩器輸出頻率和控制電壓之間并非嚴格的遵循線性關系，因此，當使用公式（2）來確定某特定輸出頻率fm的控制電壓vm時，給振蕩器施加預置電壓vm，振蕩器實際輸出頻率為fr，此時fm≠fr，并且誤差頻率能非常大，這給鎖相環路將振蕩器振蕩頻率從fr鎖定到fm增加了耗時，當誤差頻率超過鎖相環路的捕捉帶寬時，會導致鎖相環失鎖，因此尋找一種合適的算法來準確描述輸出頻率和調諧電壓之間的關系是有必要的，鑒于BP神經網絡有很強的非線性映射能力，同時原理簡單易于實現，本文提出一種使用BP神經網絡模型來描述頻率和調諧電壓之間關系的方法。

2 BP神經網絡模型的建立

2.1 BP神經網絡

BP神經網絡屬于前饋型網絡，具有很強的非線性映射能力，通常由輸入層、輸出層和若干個隱層構成[2]，結構如圖3所示。

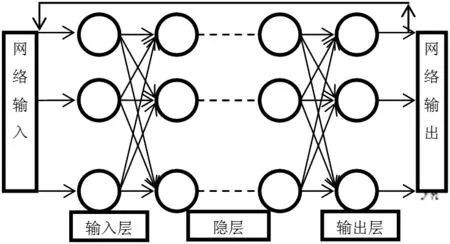
圖3 BP神經網絡結構圖

神經網絡的基本組成單元為神經元，同一層神經元中沒有任何耦合，每一節點的輸出只影響下一層節點的輸出。網絡的學習過程由正向和反向傳播兩部分組成。第k層第i個神經元的結構如圖4所示。

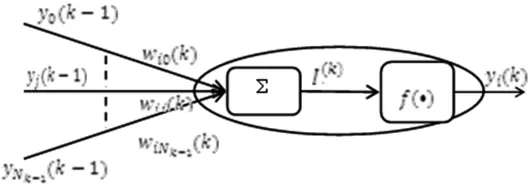
圖4 神經元結構圖

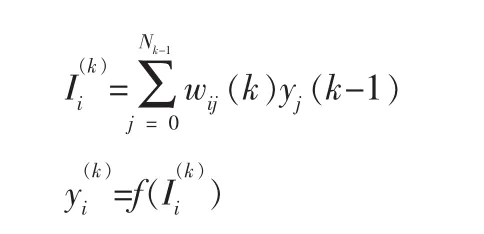
f（·）為作用函數，一般取硬限幅函數或Sigmoid函數，本文中擬采用Sigmoid函數，其定義如下：

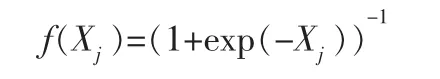
其中，Xj=ΣWijXi

2.2 BP神經網絡學習算法

對于給定的總層數為P的BP神經網絡，其學習樣本集為（（Xl，Dl），l＝1，2，…，S，網絡學習的目的為求各層的權系數Wij（k），k＝1，2，…，P，使全局誤差 E 達到最小值。 其中 n 為輸出神經元個數。

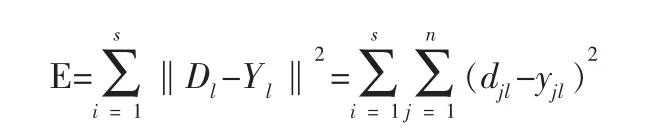
在開始訓練時，網絡的全部權值必須初始化，一般設置為較小的隨機數，這可保證不因權值取最大值而使網絡出現飽和或出現反常情況。

BP算法的訓練步驟如下：

1）從樣本集中取一樣本對，把輸入矢量用作網絡的輸入；

2）計算網絡輸出矢量；

3）計算網絡輸出矢量與樣本對的目標矢量的差；

4）再從輸出層反向計算到第一中間層，向減少差錯方向調整網絡權值；

5）對樣本集中每一個樣本對重復上述1至4步，直到整個樣本集的差錯最小。

學習結束是指實際輸出矢量與目標矢量間差錯已減少到可接受的值，權值已不再調整。

權值的調整根據Delta規則進行。

Wij（n＋1）＝Wij（n）＋ηδjX′j

其中，Wij（n）為神經元i至神經元j的第n次變更的權值，X′j為神經元i的輸出，η為學習率常數，δj為神經元j的差值。如何向減少差錯方向調整權值是關鍵，BP算法一般是采用梯度下降原理，即在權值空間中沿梯度方向搜索。有關BP算法的更詳細知識可參考文獻[3]。

3 實驗結果與討論分析

在本實驗中，輸入矢量和輸出矢量均為1維，中間層數和每一層神經元個數選的太少，不利于網絡的學習，選的太多，雖然會提高模擬精度，但是會影響工作效率，因此，綜合考慮，采取折衷，兼顧效率和精度。每層神經元的個數選取10個，中間層選取4層，權值調整算法采用梯度下降算法。本文中使用的信號發生器壓控振蕩器振蕩器輸出頻率范圍是5GHz～10GHz，調諧電壓范圍是 0～20v，訓練輸入樣本集采用在整個頻率范圍內隨機抽取100個樣點，開發環境為VC2005，首先使用樣本集中的樣點訓練神經網絡，通過迭代的方法計算出各個神經元之間的權值，然后將神經網絡應用到信號發生器中，設置要輸出的頻率，神經網絡將會計算出壓控振蕩器對應該頻率的電壓值，將該值送到設置振蕩器調諧電壓的寄存器，振蕩器將會起作用輸出設置頻率，各個頻點的設置結果如圖5所示。

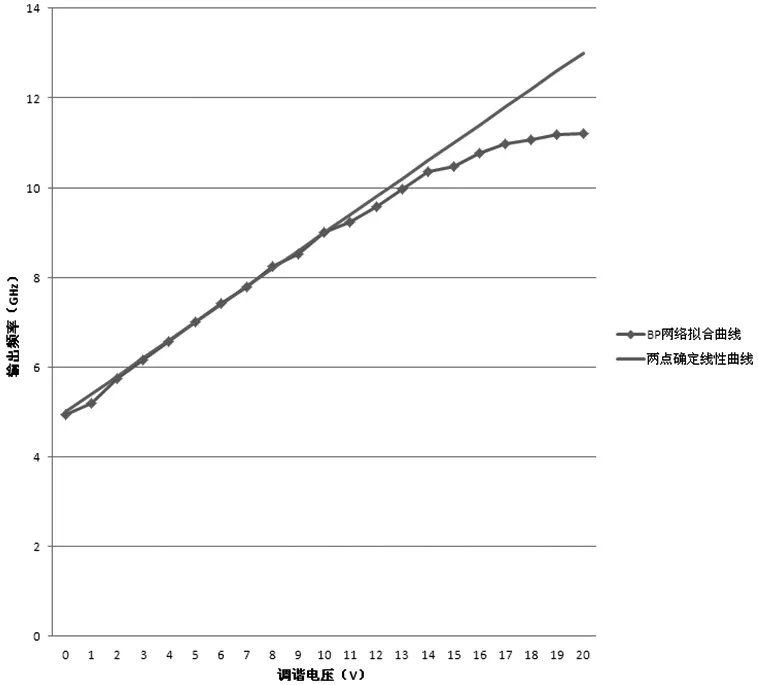
圖5 BP網絡擬合曲線與線性曲線對比圖

與圖1對比可以看出采用BP神經網絡雖然不能完全逼近圖1中的曲線，但是相對于直線已經有很大改觀。

4 小結

通過構造簡單的BP神經網絡來擬合振蕩器輸出頻率與調諧電壓之間的關系，擺脫了振蕩器輸出高端和低端的非線性，在點頻模式下能夠準確的輸出預置頻率，縮短了鎖相環路的工作時間，提高了工作效率。但是在掃頻時由于磁滯現象的存在，掃速的不同會導致不同的非線性曲線，該問題有待于從理論和應用方面進一步認識和研究。

［1］信息產業部電子41研究所.現代通信測量儀器[M].北京：軍事科學出版社,1999：39-52.

［2］王偉.人工神經網絡原理：入門與應用[M].北京：北京航空航天大學出版社,1995：100-105.

［3］楊行峻,鄭君里.人工神經網絡[M].北京：高等教育出版社,1991：70-76.