數學建模在高職數學教學中的應用分析
馬提寶
(黑龍江農業經濟職業學院,黑龍江 牡丹江 157041)
數學建模在高職數學教學中的應用分析
馬提寶
(黑龍江農業經濟職業學院,黑龍江 牡丹江 157041)
高等職業院校擔負著培養學生實際應用能力和動手操作能力,使高職學生成為行業基層型的應用人才的重任。因此,高職院校的教學必須重視教學內容的實用性。數學建模是數學知識應用于實際生活的重要手段和工具,在高職數學教學中向學生貫徹數學建模的思想高度契合高職院校的教學目標和人才培養標準。本文重點分析和探討了數學建模在高職數學教學中的應用情況。
數學建模;高職數學;實際應用
前言
數學建模是利用數學語言和數學方法來表述被研究對象的內在規律,建立起與之相適應的模型,并利用軟件程序等方式來進行求解,將獲得的結果應用到實際問題的處理和解決過程中。當前,各行各業為了提高決策的科學化,需要利用定量分析的方式來為其提供決策支持,所以數學建模在實際生活和工作當中有重要的應用價值。利用數學建模的方式可以將實際問題和數學知識有機地聯系起來,在高職數學教學中進行數學建模的相關教學和訓練符合高職院校教學改革的要求和人才培養標準。
1.高職數學教學的現狀分析
目前,不少高職院校的數學教學仍采用傳統的教學模式,即重視理論知識的傳授而忽視應用技能的培養。這種教學模式顯然不符合高職院校以培養學生職業技能為主的教學目標。綜合來看,目前高職院校的數學教學存在著以下幾點不足:
首先,依然非常重視培養學生數學知識體系的完整性和系統性,而對于數學學科與其它學科之間的聯系和滲透則涉及的較少或者程度不深,對于培養高職學生在綜合運用數學知識方面存在著一定程度的約束和限制作用。其次,教學內容傾向于古典,對于現代數學則沒有能夠給予足夠的重視。具體表現為,在數學教學中重視知識的連續性,而忽視知識的運用技能;重視數學的分析和推導,而忽視數值的運算;重視計算技巧的教授,而忽視數學思想的培養。再次,課程模式過于單一,教學內容缺乏與時俱進的更新,在利用現代教學手段培養學生現代數學知識方面也存在著欠缺,在滿足不同專業學生專業技能需求多樣化方面存在著較大的不足。最后,在數學教學中過度重視數學知識的縱向深度講解,而對于知識體系的橫向廣度延伸教育方面尚有欠缺,限制了學生數學視野的開拓,無法很好地培養學生解決問題的意識和能力。
總之,高職院校的數學教學模式和教學理念進行改革勢在必行,將數學建模理念融入到高職數學教學當中,對于促進高職數學課程的改革而言大有裨益。此舉不但與高職院校的教學目標和人才培養標準具有很高的契合度,更是可以直接培養并提高學生運用數學、使用數學的意識和能力。
2.數學建模在高職數學教學中的融入途徑分析
從思維過程來看,數學建模是一個富有創造性的過程,因為數學建模沒有規定的參考資料,沒有指定的參考答案,沒有一成不變的方法,有些甚至都沒有成型的數學問題,需要學生在收集和整理資料的過程中,采用綜合分析的方式對所學知識進行獨立思考,找到問題的主要矛盾或者矛盾的主要方面,通過合理假設和科學概括的方式形成數學問題,并在此基礎上分析問題特點,從多元化的角度探尋解決問題的途徑和方法,進而獲得該數學問題的結論,最后對問題的優劣、合理程度進行對比和分析。需要特別說明的是,整個數學建模及其求解的過程只求合理,重視創新,其他問題則次之考慮。學生參與數學建模能夠有效培養學生的自主學習能力、團隊合作能力、文字語言表達能力、計算機應用能力、抽象思維能力及其簡化能力、想象能力、資料和相關信息的整理與處理能力等等,所以說,數學建模培養的是學生的綜合能力。
構建一個符合高等職業教育目標的數學課程體系是在高職數學教學中應用數學建模的基礎和關鍵環節,該課程體系見圖1。
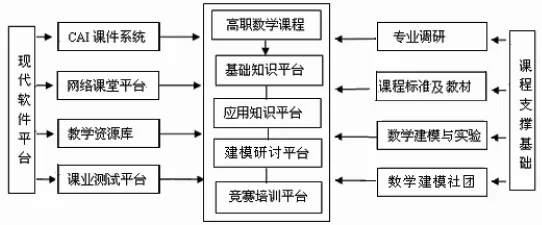
圖1 符合高等職業教育目標的數學課程體系示意圖
能否在真正意義上做到珍惜、發現并激發學生的各種潛能,是高等職業院校達成其能力培養、職業教育以及價值觀訴求目標的關鍵性因素。將數學建模的相關研討會視為高職數學教學課程體系一個重要的構成模塊。在此基礎上,我們將研討內容、評價方案以及課程安排納入到目前的高職數學課程標準當中,通過數學建模作業的方式來搭建學生學習和研究數學建模的平臺,綜合運用多種學習措施,如學生自學、教師指導、資料收集、文獻閱讀、數據處理、分析假設、團隊合作、問題處理、問題解決以及演講答辯等。這些方式讓高職院校的學生對于數學建模有了初級層面的了解和體驗,通過后續不斷地開發和體驗,讓學生在最大程度上開發他們的潛能。
好的教學模式需要與之配套的評價方案。在評價方式方面,“知識、素質、能力”的多元化評價標準取代了過去以“知識(分數)”為主的評價模式,同時,為了能夠在真正意義上落實并執行該評價方案,需要制定教師和學生評委都可以簡單操作的量化標準細則和相關指標。由于評價內容放棄了傳統的單純知識性考核,其評價結果也就顯得更加科學合理。新的評價方案倡導采用“知識分析、解決問題”的考核模式,能夠衡量和考核學生在學習過程中的動態發展歷程,例如,分工狀況、資料和文獻收集與查閱狀況、數學知識和方法的綜合運用能力、溝通交流能力、團隊協作能力、創新能力、提綱的擬定、論文的撰寫、PPT的制作等。另外,評價主體也采用了多元化的策略,即評價總分當中,學生自評占10%,學生評委占30%,教師占60%,其中教師主要負責論文的創新性、合理性、表述清晰度以及論文形成過程的學生表現等指標的評分,而學生評委則負責PPT制作水平和質量、主講演示、答辯表現、語言表述、論文結構和思路、團隊協作、應變能力等指標的評分,學生自評參考學生評委的評分指標進行。同時規定,數學建模部分的分數占學生期末總成績的30%。
3.數學建模在高職數學教學中的實踐
由于學習基礎相對空白和高職學生對于抽象分析方法的接受遠不如對直觀圖形的認識來得迅速,而具備繪圖功能的數學軟件MABLAB為此提供了一個巧妙的平臺。給學生演示圖形的繪制并引導他們親自動手,及早掌握利用MATLAB等軟件繪制圖形的方法不但能夠加強其對數學理論本身的理解,而且對日后他們可能參與的建模實踐也可起到先導作用。例如,使用MATLAB程序就可以繪制出心臟線或星形線的圖案(見圖2和圖3),這些圖形用古老的“描點法”是難以實現的。
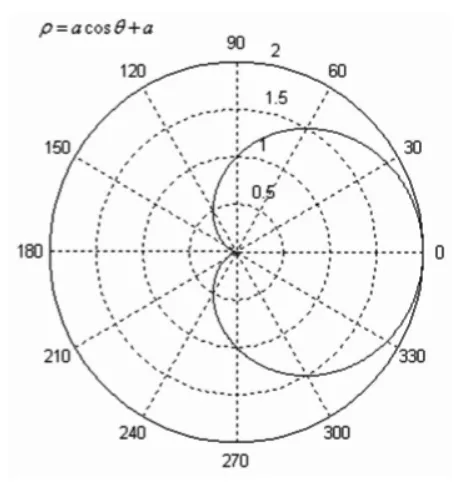
圖2 (左),使用MATLAB程序繪制出的心臟線示意圖

圖3 (右),使用MATLAB程序繪制出的星形線示意圖
講到遞歸函數時,引入古老而有趣的“斐波那契數列與野兔生子”問題:兔子出生以后兩個月就能生小兔,如果每月生一次且恰好生一對小兔(雌雄各一只),且出生的兔子都成活,試問n年后有多少對兔子?兔子的數目構成優美的斐波那契數列模型,滿足遞推公式:
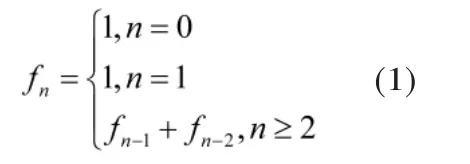
那么這個數列的通項公式怎么寫?它可以應用在哪些領域?一個基于實用主義的數學模型造就出一個漂亮的序列,這個序列不再是閉門造車的產物,而有了活生生的應用背景。
雖然都是正整數,可是它們卻由一些無理數表示出來:
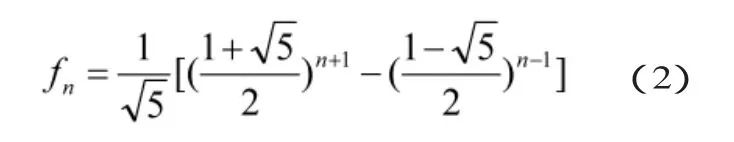
在微積分的應用實例中,培養學生應用極限、相對變化率、微元等思想,建立函數關系、微分方程等。在線性代數的應用實例中,培養學生用矩陣與線性方程組來解決問題。在概率統計的應用實例中,培養學生處理隨機問題的方法,應用期望值和標準差描述隨機現象的特征,對統計數據的處理和分析做出推斷的方法。
4.結束語
將數學建模的思想和方法融入高職數學的教改實踐,無疑會成為促進全面協調可持續發展的素質教育的重要載體,必定能為高等職業教育的又好又快發展發揮積極的作用。
[1]馮寧.數學建模融入高職數學教學體系的理論探索與實踐研究[J].常州輕工職業技術學院學報,2009,(04):136-138.
[2]黃金偉.數學建模融入高職數學教學的探索與實踐[J].福建信息技術教育,2010,(01):109-110.
[3]萬萍.高職數學建模活動模式的實踐與探索[J].國土資源職教改革與創新,2009,(Z1):163-167.
[4]鄧通德.滲透數學建模思想的教學探討[J].國土資源高等職業教育研究,2006,(04):326-328.
[5]萬里亞.將數學建模思想融入高等數學課程中的探討[J].常州工程職業技術學院學報,2008,(04):256-257.
[6]郭嵩.數學建模與“問題解決”的數學教育思想[J].淮陰師范學院教育科學論壇,2008,(01):203-204.
[7]岳玉靜,何冰潔,王國強,蔡新中.談數學建模思想在高職高等數學教學中的滲透[J].上海工程技術大學教育研究,2009,(01):125-126.
G712
A
1008-7508(2012)08-0079-02
2012-04-19
馬提寶(1979—),黑龍江雞東人,講師。研究方向:高等數學。