吃透考綱精神,把握命題規律
☉湖北省武漢市黃陂區第一中學 盧 瓊(特級教師)
《2012年普通高等學校招生全國統一考試湖北卷考試說明》數學科部分(以下簡稱《考綱》)終于與大家見面了,今年我省數學《考綱》的各項要求明確具體.解讀《考綱》,關注其蘊含的信息,新課程高考第一年,平穩過渡,無縫對接,湖北省今年高考數學命題風格較往年變化不會太大;學習《考綱》,重點分析考試性質、命題指導思想、考核目標與要求、考試范圍與要求層次;研究《考綱》,明確它在強化什么、淡化什么、回避什么,加深課程改革和高考改革一致性的認識,樹立高三復習教學新理念.
筆者在文中將結合教學實例,以題源的呈現、題源的解析、題源的探究、題源的變式與拓展為主線,淺談如何立足于課本,吃透考綱精神,把握命題規律這一主題.
一、領會《考綱》的命題思想,在回歸梳理中尋找題源
《考綱》的命題指導思想是:命題遵循《普通高中數學課程標準(實驗)》和《2012年普通高等學校招生全國統一考試大綱(課程標準實驗版)》,試題在源于教材的同時又具有一定的創新性、探究性和開放性,既考查考生的共同基礎,又考查考生的學習潛能,以滿足選拔不同層次考生的需求.
課本是高考試題的重要來源,很多高考試題都是由課本例題和習題改進、改型、綜合、引申、演變而來,翻開近幾年湖北高考試卷,無論文理科均有100分左右的題目源于教材,兌現了《考綱》的承諾.因此,我們在復習教學中,引導學生回歸課本,梳理教材,在課本的例題和習題中尋根探源,讓學生跳出題海,不做題奴,走高效備考之路.
題源呈現設f(α)=sinxα+cosxα,x∈{n|n=2k,k∈N*},利用三角變換,估計f(α)在x=2、4、6時的取值情況,進而對x取一般值時f(α)的取值范圍作出一個猜想.
這是人教版數學教材《必修4》習題3.2B組中的第5題(第157頁),主要考查三角函數的基本知識、三角恒等變形的基本技能和代數推理的基本方法,此題看似平凡,但設問方式不落俗套,既具開放性又具探究性,給人以無限想象的空間,留下進一步研究的接口,必然深受高考命題人青睞.如果我們在教學中,也能充分利用這些素材,開發這些資源,幫助學生理解掌握常規思維、常規解法,那必將引導考生走向高考成功.
二、明晰《考綱》的知識要求,在內化融合中落實目標
《考綱》的知識要求是:要求對所列知識的含義有初步的、感性的認識;對所列知識內容有較深刻的理性認識,知道知識的邏輯關系,能夠對所列知識作正確的描述說明并用數學語言表達,能夠利用所學的知識內容對有關問題進行比較、判別、討論;系統地掌握知識的內在聯系,能夠利用所學知識對具有一定綜合性的問題進行分析、研究、討論,并加以解決.
明晰《考綱》的知識要求,敦促學生加強對課本知識的內化吸收,夯實基礎,并牢固地掌握重要的數學思想方法;提醒學生加深對課本例題和習題內在聯系的整理融合,形成更加完備的知識網絡和方法體系,真正實現課程的三維目標(知識與技能,過程與方法,情感態度與價值觀).
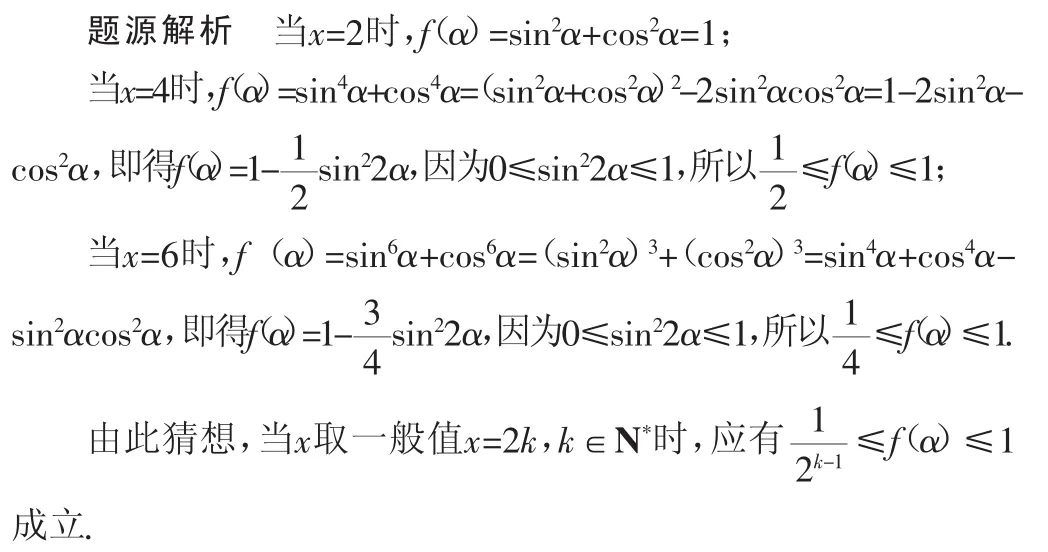
本題從同角三角函數的基本關系式出發,在x=2、4、6時,借用代數公式,進行三角恒等變形,簡化f(α)的表達式,再利用正、余弦函數的有界性,估計f(α)的取值情況,通過觀察式子的結構特征,品味式子的數據特點,聯想類比,合情推理,猜想得出f(α)的取值范圍的一般表達,但問題的解決遠未結束,猜想正確性的判定,還有待我們進一步探求,整個過程環環相扣、引人入勝.
三、理解《考綱》的能力要求,在探究分析中培養能力
《考綱》的能力要求是:高考考查空間想象能力、抽象概括能力、推理論證能力、運算求解能力、數據處理能力以及應用意識和創新意識;強調探究性、綜合性、應用性,突出數學試題的能力立意,堅持素質教育導向.
為此,我們在教學中,應強化解題過程的研究,解題方法的提煉,解題思想的滲透,精心設計一題多解、一題多變、多題一解等訓練,引導學生觀察、聯想、討論、對比、質疑等實踐操作,積極探索解決問題的最佳途徑,讓學生在探究分析中提高應變能力,激發創新潛能.
題源探究 在α∈R、n∈N*的條件下,證明不等式
事實上,因為0≤sin2α≤1,所以當n∈N*時,sin2nα≤sin2α,同理cos2nα≤cos2α,由此可得,sin2nα+cos2nα≤1.
下面只需證明在α∈R、n∈N*的條件下,不等式
探究途徑一、在初等數學范疇內,用數學歸納法求證.
當n=1時,命題成立.

由此可見,這道練習題的編制,專家是煞費苦心的,把題目的基礎部分放在必修4,把深入探究的內容植入選修2-2,循序漸進,螺旋上升,體現出開放性、探究性的新課程理念,而數學歸納法是《考綱》中規定考查的內容,應引起我們高度重視.
探究途徑二、在高等數學觀點下,用凸函數性質解題.
當n∈N*時,構造函數F(x)=xn(x≥0),求其二階導數,即得F″(x)=n(n-1)xn-2≥0,因此,函數F(x)=xn區間[0,+∞)上是一個下凸函數.
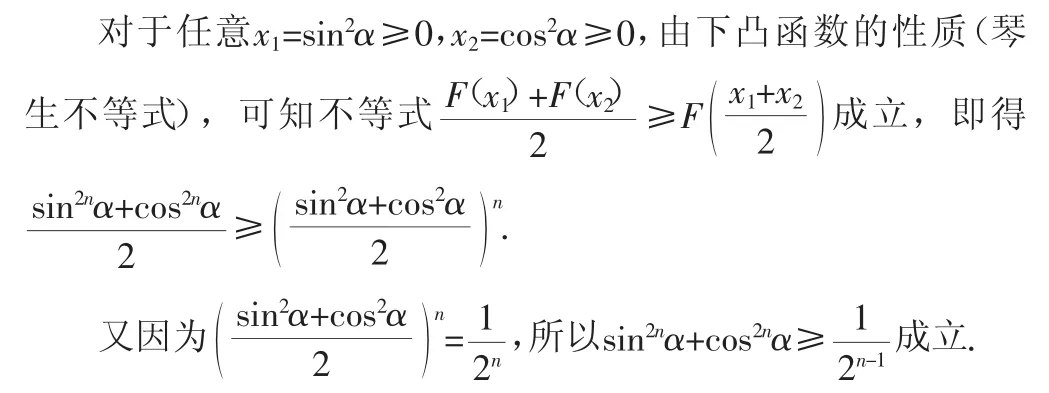
從對題源的探究分析,可知在不同的背景下,運用不同的知識,從不同的角度思考,得到不同的解法,體現出不同的能力要求.
四、體味《考綱》的考查要求,在變式拓展中增長見識
《考綱》的考查要求是:注重試題的基礎性、綜合性和層次性,堅持多角度、多層次的考查;對數學思想和方法的考查與數學知識的考查結合進行,考查時,從學科整體意義和思想含義上立意.
《考綱》的考查要求告誡我們:對于問題的探究,絕不能淺嘗輒止,以得到答案為滿足,而應為此作進一步挖掘、多方位求索、有機演變和拓展引申,求新求異,在變式中求拓展、在拓展中覓規律,提高學生分析問題和解決問題的能力,培養學生良好的思維習慣.
從式子sinρα+cosρα的結構看,與題源相似,而sin2α+cos2α=1,且因此轉換思考角度,可令

該題源的探究也可另辟蹊徑,構造函數g(x)=xn+(1-x)n(0≤x≤1),研究性質加以證明,這樣一來,學生就會在問題的解決中,豐富思路、開闊眼界、增長見識.
題源拓展 若a>0,b>0,λ∈R,且λ≠0,λ≠1,滿足aλ+bλ=m,那么:
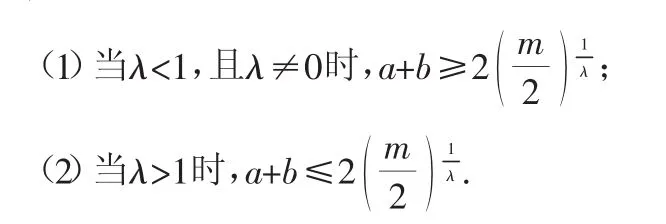
這是《數學通報》第1792號數學問題,乍一看,aλ+bλ=m的結構與題源沒有關聯,但仔細觀察結論,又似曾相識,經過轉換,就現廬山真面目.

結合實例,研習《考綱》,我們更加明確高考試題是如何體現在數學知識網絡的交匯點和能力層次的交叉區處命題的,也更加明確高考試題是如何多視點、多角度、多層次地考查考生的數學素養和潛能的,同時還知道高考試題的設計總是在想辦法客觀地反映考生的數學視野、審慎思維的習慣和堅忍不拔的科學態度的.

