中考數學思想方法總結
☉云南省紅河州彌勒縣西山民族中學 楊 鳳
中考第二輪復習以專題復習為主線,使學生在系統掌握基礎知識和基本技能的基礎上形成基本的數學思想方法,使之達到系統化、結構化、完整化,進而掌握通性、通法,進一步提高學生分析問題和解決問題的能力.數學思想比較豐富,初中常見的數學思想有五大類:函數的思想、方程的思想、數形結合的思想、分類討論的思想和轉化的思想.思想是數學的靈魂,是對數學內容的本質認識,方法是思想的體現,有什么樣的思想就有什么樣的方法,由于思想和方法的高度統一,有時稱為“數學思想方法”.下面通過分析和探究部分中考題的解法,對中考數學蘊含的思想方法作五個方面的總結.
一、函數的思想
函數的思想是用運動變化的觀點分析問題和研究數量關系,也是用已知函數模型的圖像和性質去分析問題、轉化問題和解決問題.
例1 (2011年山東濟寧市)如圖1,是張老師出門散步時離家的距離y與時間x之間的函數關系的圖像.若用黑點表示張老師家的位置,則張老師散步行走的路線可能是( ).
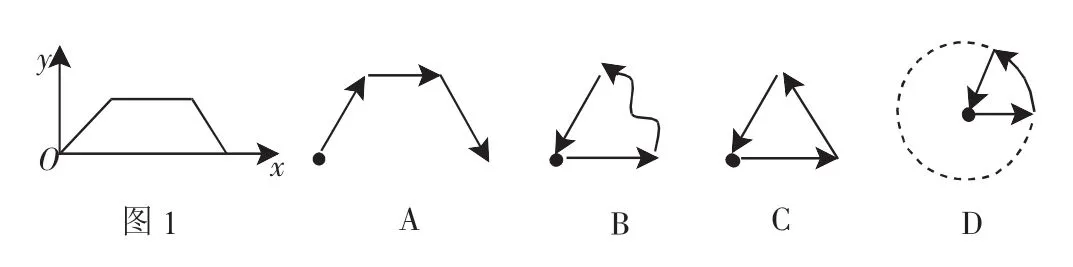
分析:圖1是“距離-時間”圖象,根據距離隨時間的運動變化來想象和確定行走路徑.
解析:由圖1知道,最終距離為0,說明行走后回到出發點,有一段路程隨時間的變化而不變,說明行走在圓弧上.故選D.
點評:本題著重考查看圖識圖能力,首先要弄清楚是什么關系圖,其次要根據圖象進行分析和對應的想象.
例2(2011年四川南充市)小明乘車從南充到成都,行車的平均速度y(km/h)和行車時間x(h)之間的函數圖像是( ).

分析:根據已知條件建立函數關系,再根據函數模型確立函數圖像.
解析:設南充到成都的距離是Skm,則行車的平均速度y(km/h)和行車時間x(h)之間的函數關系是因為S>0,所以由反比例函數圖象知道選B.
點評:本題以實際行程為背景考查反比例函數的圖像,需要能夠根據實際問題建立函數關系,并運用函數模型解決問題.
二、方程的思想
方程的思想是從問題的數量關系入手,運用數學語言將問題中的條件轉化為方程(組),通過解方程(組)使問題得到解決.
例3(2011年云南玉溪市)2006年我市在全國率先成為大面積實施“三免一補”的州市.據悉,2010年我市籌措農村義務教育經費與“三免一補”專項資金3.6億元(由中央、省、市、縣(區))四級共同投入,其中,中央投入的資金約2.98億元,市級投入的資金分別是縣(區)級、省級投入資金的1.5倍、18倍),且2010年此項資金比2009年增加1.69億元.
(1)2009年我市籌措農村義務教育經費與“三免一補”專項資金多少億元?
(2)2010年省、市、縣(區)各級投入的農村義務教育經費與“三免一補”專項資金各多少億元?
(3)如果按2009-2010年籌措此項資金的年平均增長率計算,預計2011年,我市大約需要籌措農村義務教育經費與“三免一補”專項資金多少億元(結果保留一位小數)?
分析:(1)根據“2010年此項資金比2009年增加1.69億元”可以列式求解;(2)根據“三免一補”的資金投入總和可以列出方程;(3)根據年增長率的計算公式:,求出下一年的專項資金.
解析:(1)2009年我市籌措農村義務教育經費與“三免一補”專項資金是3.6-1.69=1.91(億元).
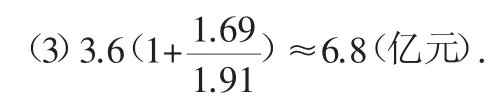
答:(1)2009年我市籌措農村義務教育經費與“三免一補”專項資金1.91億元;(2)省、市、縣(區)分別投入資金為0.02億元、0.36億元、0.24億元;(3)預計2011年我市約籌措專項資金6.8億元.
點評:解決該問題需要通過閱讀發現等量關系,并找出數量之間的相互關系,如市級投資是縣級的1.5倍,市級投資是省級的18倍,即縣級投資和省級投資是以市級投資為連接點,若設市級投資為x億元,則縣級投資為億元,省級投資為億元.根據已知條件中的總投資關系建立起等量關系,從而問題得到解決.
例4(2011年湖南常德市)某城市規定:出租車起步價允許行駛的最遠路程為3千米,超過3千米的部分按每千米另收費.甲說:“我乘這種出租車走了11千米,付了17元”;乙說:“我乘這種出租車走了23千米,付了35元”.請你算一算這種出租車的起步價是多少元?以及超過3千米后,每千米的車費是多少元?
分析:甲和乙說的兩句話就是兩個等量關系,根據這兩個等量關系建立方程,問題便迎刃而解.
解析:設這種出租車的起步價是x元,超過3千米后每千米收費y元,根據題意得:

答:這種出租車的起步價是5元,超過3千米后每千米收費1.5元.
點評:這個問題涉及起步價和超過價,需要弄清楚它們之間的關系,并把已知的等量關系轉化為數學符號建立方程.
三、數形結合的思想

圖2
數形結合的思想是在數和形之間建構一座橋梁,形成一一對應關系,既分析數量關系,也揭示幾何意義,化抽象為具體,“以形助數”,“以數解形”,代數問題幾何化,幾何問題代數化,從而看透問題的本質.華羅庚說過:數缺形時少直觀,形缺數時難入微,數形結合百般好,隔裂分家萬事休.
例5 (2011年吉林長春市)在長為10m、寬為8m的矩形空地中,沿平行于各邊的方向分割出三個全等的小矩形花圃,其示意圖如圖2所示.求小矩形花圃的長和寬.
分析:由于圖形中的三個矩形花圃全等,即三個矩形花圃的長和寬分別都相等,根據三個矩形花圃和大矩形的位置關系得出數量關系,即兩個花圃的長與一個花圃的寬等于矩形的長,兩個花圃的寬與一個花圃的長等于矩形的寬,列出方程組求解.
解析:設小矩形花圃的長為xm,寬為ym.
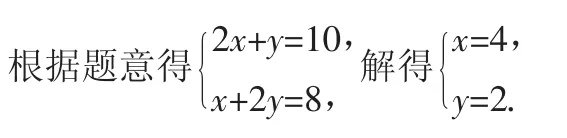
答:小矩形花圃的長為4m,寬為2m.
點評:本題以現實生活中的幾何圖形為背景考查圖形的位置特征與數量關系,關鍵是“以形助數”,幾何問題代數化,根據幾何圖形的位置特征和數量關系列出方程組,從而解決問題.
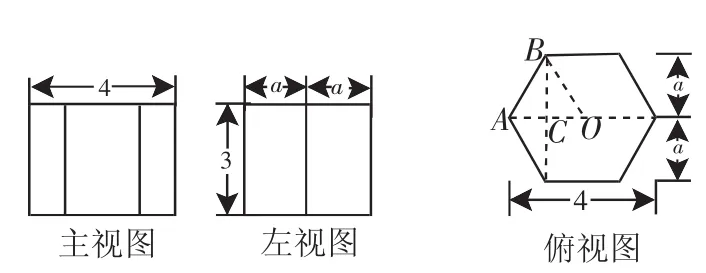
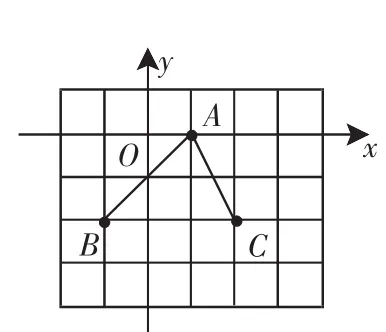
A.6 分析:先分別求出關于x的不等式的解集,再根據其他條件,結合數軸確定m的取值范圍. 解析:由x-m<0得x 圖3 因為不等式組的解包含4個整數,所以m的取值范圍是6 點評:本題要借助數軸由數到形進行觀察分析,“以形助數”使問題得到解決. 分類討論的思想是在解答某些數學問題時,有時會遇到多種情況,需要對各種情況加以分類,并逐類求解,分類討論遵循的原則是統一標準,不重復和不遺漏. 圖4 例7 (2011年江西省)在直角坐標系中,已知A(1,0)、B(-1,-2)、C(2,-2)三點坐標,如圖4所示,若以A、B、C、D為頂點的四邊形是平行四邊形,那么點D的坐標可以是________(填序號). ①(-2,0) ②(0,-4) ③(4,0) ④(1,-4) 分析:由于以A、B、C、D為頂點的四邊形是平行四邊形的位置有三種情況,故需要一一討論確定點D的坐標. 解析:⑴以AB和BC為鄰邊的平行四邊形時,根據圖6作出點D,求得點D的坐標是(4,0); ⑵以AB和AC為鄰邊的平行四邊形時,根據圖6作出點D,求得點D的坐標是(0,-4); ⑶以AC和BC為鄰邊的平行四邊形時,根據圖6作出點D,求得點D的坐標是(-2,0).故填①②③. 點評:本題以△ABC為基礎的平行四邊形存在三種情況,需要按位置分類解決,考慮問題要周密,否則易漏解. 轉化的思想就是對一個問題等價地換一種方式、角度或觀點來處理,化陌生為熟悉,化復雜為容易,化抽象為具體,化未知為已知,化實際問題為數學模型.有的數學問題只有不斷地進行等價轉化才能解決. 例8 (2011年湖北荊門市)如圖5,長方體的底面邊長分別為2cm和4cm,高為5cm.若一只螞蟻從P點開始經過4個側面爬行一圈到達Q點,則螞蟻爬行的最短路徑長為_______cm. 圖5圖6 分析:由于螞蟻爬行的路徑是折線,每一條線段的長無法算出,這就需要把部分合為整體考慮,將路徑展開在一個平面上作為整體考慮. 解析:將長方體沿PQ展開側面,如圖6所示.由勾股定理算得最短路程PQ是13cm,故螞蟻爬行的最短路徑長為13cm. 點評:本題考查了把部分轉化為整體,用整體求路程的方法.當直接求部分行不通時,可以考慮部分構成的整體. 例9 圖7是一個正六棱柱的主視圖和左視圖,則圖中的a=( ). 圖7圖8 分析:要計算a的值就必須將數據轉化到俯視圖中,根據正六邊形的性質進行計算. 解析:根據主視圖和左視圖中的數據,作出俯視圖,如圖8所示. 由正六邊形的性質得AB=OA=2,BC=a,∠OAB=60°.在Rt△ABC中.故選B. 點評:在涉及三視圖時,需要根據“長對正,寬相等,高平齊”將數據在三個視圖中轉化,進而進行計算,有時是幾何體與視圖之間進行轉化. 總之,在學習數學的過程中需要不斷對方法和思想進行總結,使它上升至一個高度,形成數學思想方法,并用數學思想方法指導我們解題,這樣才能運用數學和駕馭數學,成為學習數學的真正主人.
四、分類討論的思想
五、轉化的思想