基于夏比試驗確定船用鋼板斷裂韌性

黃 一，陳景杰，劉 剛

(大連理工大學船舶學院，116024遼寧大連，chenjingjiedlut@163.com)

斷裂韌性是材料固有的特性，是描述含裂紋損傷結構是否處于安全狀態的基礎.眾所周知，當裂紋尖端的應力強度因子值大于材料的斷裂韌性時，裂紋將發生失穩擴展而導致結構斷裂.因此，評估含裂紋損傷船體結構的安全狀態時，需要確定船用鋼板的斷裂韌性值.船用鋼板通常采用普通強度鋼和高強度鋼兩種.這兩種鋼板按質量分為4個等級［1］，對于同一強度不同質量等級的鋼材，其強度性能相同，僅是材料的斷裂韌性不同.因此，確定船用鋼板的斷裂韌性時，需要研究不同強度不同質量等級對應的斷裂韌性值.目前“金屬材料平面應變斷裂韌性KIC試驗方法”［2］被認為是測量材料斷裂韌性值精度最高的方法，已作為標準準則在實驗中應用.但是該方法存在試驗尺寸大、周期長、費用高等缺點，用它評定工程材料的斷裂韌性十分困難.因此，長期以來，眾學者試圖尋找一種能夠滿意的工程精度的簡便方法，通過簡單的試驗，即可估計出材料的斷裂韌性值，其中研究最多的是夏比V型缺口沖擊試驗［3］，其試驗示意圖如圖1所示，即用規定高度的擺錘對處于簡支狀態的V型缺口試驗片進行一次性沖擊，測量試驗片折斷時的沖擊吸收功.

由于夏比V型缺口沖擊試驗方法費用低廉、速度較快等優點，盡管其沖擊特性值的力學意義不明確，船用鋼板的抗斷裂能力仍舊采用沖擊試驗吸收能描述.因此，為了獲得船用鋼板的斷裂韌性值，需要建立材料吸收能和斷裂韌性二者之間對應關系.國內外學者針對各自所研究的金屬材料已提出多種吸收能與斷裂韌性二者之間的函數關系［4-7］.然而，這些函數關系由于各自的局限性，無法推廣到船用鋼板等其他材料.

圖1 夏比Ⅴ型缺口沖擊試驗示意

本文根據日本造船研究會和日本焊接協會所確定的規范，利用矢導浩［8-9］給出的試驗數據，由船用鋼板吸收能計算出大量不同板厚和使用溫度下船用鋼板對應的斷裂韌性值，進而擬合出材料斷裂韌性與鋼板厚度和使用溫度之間的函數關系，為含裂紋構件安全狀態的評估提供依據.

1 基于沖擊試驗吸收能確定船用鋼板斷裂韌性

圖2和圖3是日本三菱重工技術部長崎研究所的矢島浩教授針對不同質量等級的普通強度和高強度的船用鋼板所做的夏比V型缺口沖擊試驗數據.試驗材料及試驗溫度如表1所示.

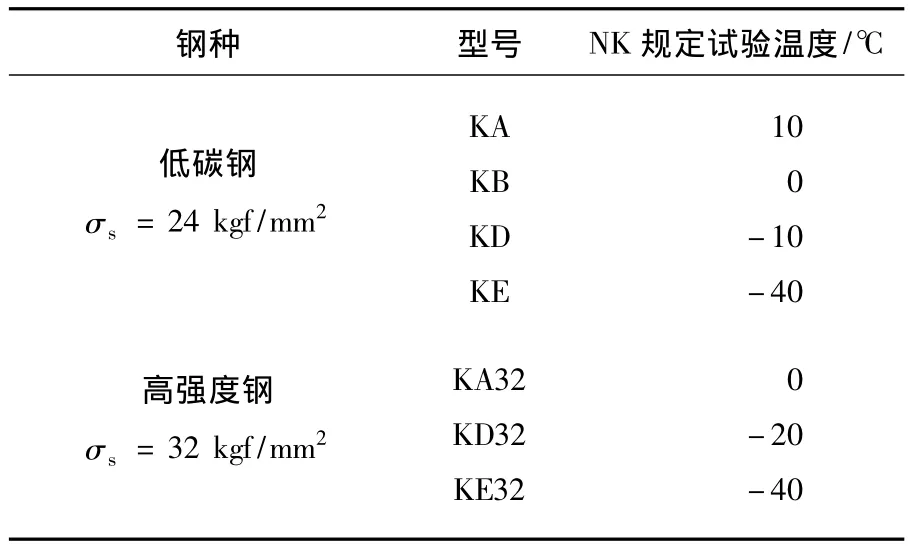
表1 試驗材料的類型及溫度

圖2和圖3中縱坐標表示夏比Ⅴ型缺口擺錘沖擊試驗吸收能的測量值，橫坐標表示不同材料各自的試驗溫度與相應的韌脆轉變溫度的差值.采用這樣的橫坐標，能夠消除不同型號鋼板在夏比Ⅴ型缺口擺錘沖擊試驗中的差異，使試驗結果服從公式(1)所示的分布規律［10］.

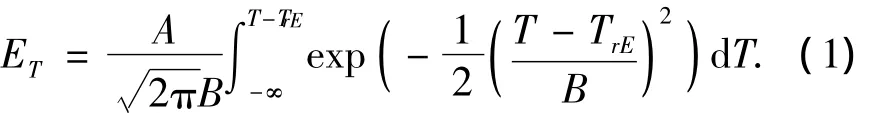
式中:A、B是兩個常數;T是試驗溫度;TrE是50%沖擊吸收能轉變溫度，記為韌脆轉變溫度;ET是沖擊試驗吸收能.

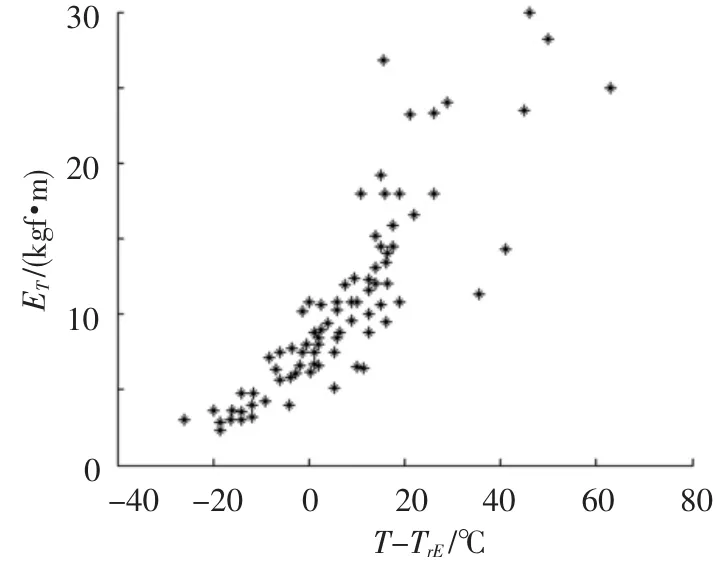
圖2 基體金屬的試驗數據

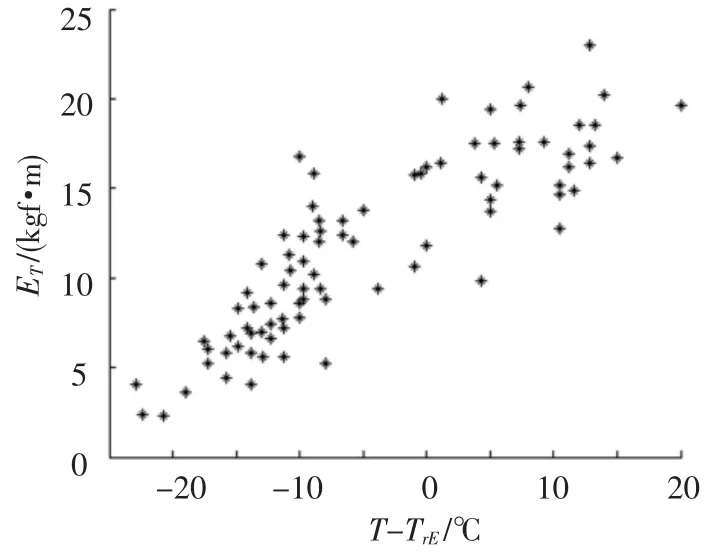
圖3 焊縫金屬的試驗數據

基于上述試驗數據和矢導浩教授所介紹的確定材料斷裂韌性的方法［8］，實現了由沖擊試驗吸收能確定船用鋼板斷裂韌性值的方法，如圖4所示.

圖4 材料斷裂韌性評價的基本過程

圖4涉及公式如下:

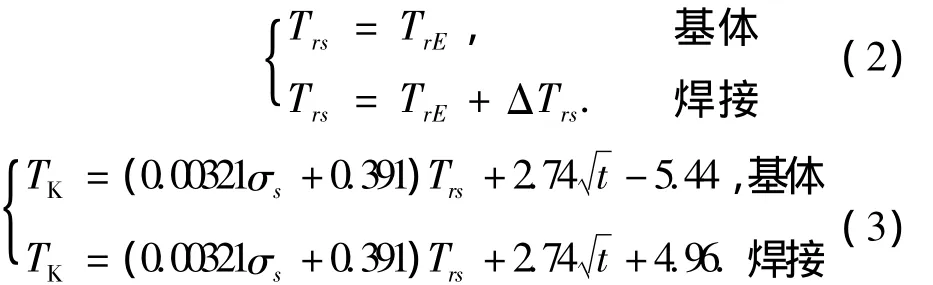
式中:Trs是50%脆性斷面率轉變溫度，記為脆斷轉變溫度，℃;TK是日本造船界評價船用鋼板斷裂韌性方法中鋼板斷裂時對應的溫度，K;t是鋼板厚度;σs是屈服極限;k0和K0為常數.

ΔTrs的取值如下:ΔTrs=25(手工電弧焊、低碳鋼)，ΔTrs=40(埋弧焊、低碳鋼)，ΔTrs=30(手工電弧焊、高強度鋼)，ΔTrs=55(埋弧焊、高強度鋼).

從圖4可以看出，根據已有試驗數據確定鋼板的斷裂韌性值，首先必須正確確定公式(1)中A、B值.采用最小二乘法原理，在保證圖5給定的擬合曲線與試驗數據之間方差最小的條件下，獲得公式(1)中A、B值.

圖5 基于不同試驗數據的擬合曲線

然后代入公式(5)中的KIC0值.KIC0表示鋼板在TK溫度下所對應的斷裂韌性值.它是根據日本造船界以圖6所示的船用鋼板進行斷裂韌性值測量試驗［1］獲得的.該試驗的基本方法是:保持外加載荷不變，逐漸降低試驗溫度而使鋼板斷裂.由于試驗模型近似為無限大板，因此可以確定鋼板的斷裂韌性為

由于擬合曲線的正確與否直接決定著船用鋼板斷裂韌性計算結果的可信程度.因此，將NK規范中給定的最小吸收能和對應的試驗溫度，代入圖5所示的擬合曲線中，確定不同強度不同質量等級鋼板的韌脆轉變溫度，并與規范中相應結果進行比較來驗證擬合曲線的正確性.表2僅給出基體金屬中TrE的計算結果及其比較情況，充分說明圖5中的擬合曲線是正確可靠的.

圖6 日本造船界確定船用鋼板斷裂韌性的試驗模型

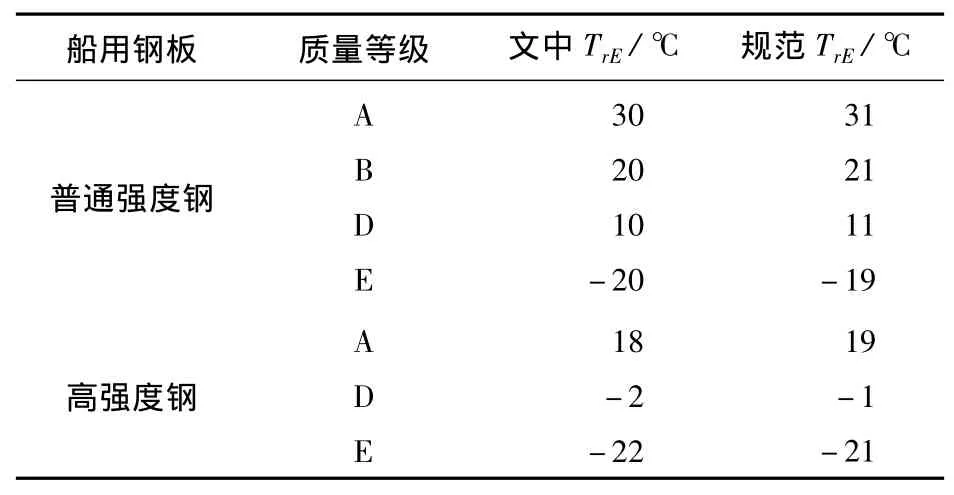
表2 不同船用鋼板的韌脆轉變溫度

2 船用鋼板的斷裂韌性

根據上述由夏比V型缺口沖擊試驗吸收能計算材料斷裂韌性的方法(見圖4)，針對不同使用溫度(T=0～-50℃)和鋼板厚度(t=10～50 mm)，對船用鋼板的斷裂韌性進行計算，得到大量船用鋼板的斷裂韌性值.本文僅列出E級高強度鋼的斷裂韌性值，結果見表3.

由表3可知，在給定的平板厚度下，船用鋼板的斷裂韌性與其使用溫度呈線性關系;在給定的使用溫度下，船用鋼板的斷裂韌性與其板厚呈近似的線性關系.

為了形象地闡述斷裂韌性與使用溫度和鋼板厚度之間的對應關系，根據表3中的數據，利用MATLAB繪制了三者之間的曲面關系，如圖7所示，可用平面來代替圖7中的曲面.

根據最小二乘法原理，采用多元一次平面擬合技術，可以得到如式(6)所示的斷裂韌性KIC與使用溫度T、鋼板厚度t的函數關系:

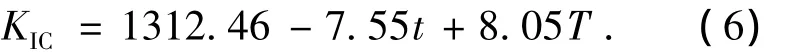
對于基體金屬和焊縫金屬中其他不同強度不同質量等級的船用鋼板，其斷裂韌性具有相似的分布規律，能夠得到與式(6)相似的表達式.

表3 基體金屬中E級高強度鋼的斷裂韌性kgf·mm-3/2

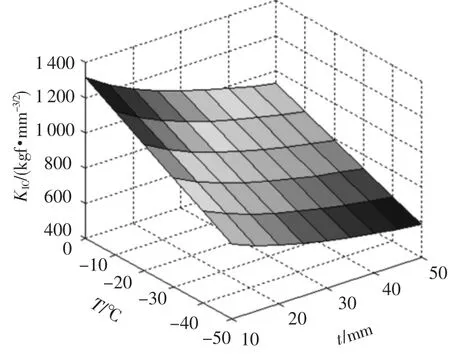
圖7 E級高強度鋼斷裂韌性值的分布

3 不同可靠度下船用鋼板斷裂韌性

由于圖2和圖3中的試驗數據(ET與T-TrE)存在較大分散性，使上述方法確定的斷裂韌性不可避免地存在較大分散性.因此，根據P-S-N曲線的思想，引入可靠度概念，根據試驗數據分別確定出不同可靠度下船用鋼板的韌脆轉變溫度及其對應的斷裂韌性.

圖5中的擬合曲線具有50%的可靠度，擬合曲線上任意點的縱坐標表示在確定的T-TrE下多次沖擊試驗吸收能的平均值.根據P-S-N曲線思想確定不同可靠度的擬合曲線時，需要獲得任意確定的T-TrE下多次沖擊試驗吸收能其對數正態分布的特征值——均方差.然而，由于在任意確定的T-TrE下實施的沖擊試驗的試驗數據總量不足，如果直接根據各試驗溫度下沖擊試驗吸收能的均值和方差來確定不同可靠度下ET與T-TrE之間對應曲線，這樣擬合的效果會因數據少而很不理想.因此，本研究以整體試驗數據為基礎，根據可靠度原理，通過式(7)，模擬出60%、70%、80%、84.1%、90%和95%不同可靠度下基體金屬和焊縫金屬相對應的整體樣本數據.

式中:ETp是p可靠度下吸收能值;ET是吸收能的平均值;σ是吸收能的均方差;up是p可靠度下正態分布值.

對于基體金屬和焊縫金屬不同可靠度的整體樣本數據，采用確定圖5中擬合曲線的方法，得到如圖8所示的不同可靠度下ET與T-TrE之間的對應曲線.

圖8 不同可靠度下對應的擬合曲線

根據圖8中不同可靠度的擬合曲線，采用“基于沖擊試驗吸收能確定材料斷裂韌性”的方法，可以確定不同可靠度下任意等級鋼板的韌脆轉變溫度.本文僅列出基體金屬對應的韌脆轉變溫度結果，見表4.

表4 不同可靠度下焊接金屬的韌脆轉變溫度

確定不同可靠度下材料的韌脆轉變溫度后，通過式(2)～式(5)，計算出不同可靠度下不同質量等級的低碳鋼和高強度鋼的斷裂韌性值，本文僅列出可靠度為90%時基體金屬中B級低碳鋼的斷裂韌性，結果見表5.

從表5中可以看出，B級低碳鋼船用鋼板的斷裂韌性值與使用溫度和鋼板厚度呈近似的線性關系.基于最小二乘原理和多元一次擬合技術，可以建立斷裂韌性KIC與使用溫度T和鋼板厚度t之間簡單的函數關系:

對于其他可靠度下，基體金屬和焊接金屬中不同強度不同質量等級的船用鋼板可獲得相似的函數關系.根據這些函數關系，采用線性插值的方法可以確定任意可靠度下(50%～95%)不同鋼板板厚和使用溫度所對應的斷裂韌性值.

表5 可靠度為90%時基體金屬中B級低碳鋼的斷裂韌性kgf·mm-3/2

4 結論

1)實現了根據夏比V型缺口沖擊試驗吸收能確定船用鋼板斷裂韌性的方法，建立了斷裂韌性、試驗溫度和鋼板厚度三者之間的函數關系，為低溫使用條件下確定任意厚度船用鋼板的斷裂韌性提供依據.

2)提出不同可靠度下ET與T-TrE之間的函數關系，建立了可靠度為60%、70%、…、95%時與鋼板厚度和試驗溫度分別呈線性關系的斷裂韌性表達式，為獲得任意可靠度下船用鋼板基體金屬和焊縫金屬的斷裂韌性值奠定基礎.

［1］陳景杰.含裂紋損傷船體結構強度分析方法研究［D］.大連:大連理工大學，2011.

［2］GB4161—84金屬材料平面應變斷裂韌性KIC試驗方法［S］.北京:中國標準出版社，1997.

［3］GB/T 229—1994金屬夏比缺口沖擊試驗方法［S］.北京:中國標準出版社，1994.

［4］BARSOM J M，ROLFE S T.Correlations between KICand charpy V-Notch test results in the transition temperature range［C］//Impact Testing of Metals，STP 466，Philadelphia:ASTM，1970:281-302.

［5］ROLFE S T，NOVAK S R.Slow-bend KICtesting of medium strength high-toughness steels，recent developments in plane strain fracture toughness testing［C］//Review of Developments in Plane-Strain Fracture Toughness Testing，STP 463.Philadelphia:ASTM，1970:124-159.

［6］SAILORS R H，CORTEN H T.Relationship between material fracture toughness using fracture mechanics and transition temperature tests［C］//Proceedings of the 1971 National Symposium on Fracture Mechanics，Part II，STP 514.Philadelphia:ASTM，1972:164-191.

［7］ROBERTS R，NEWTON C.Interpretive report on smallscale test correlations with KICdata［J］.Welding Research Council Bulletin，1981，265:1-18.

［8］矢島浩.船體用鋼板の破壊靭性値推定手法に関する-考察［R］.長崎:三菱重工業(株)技術本部長崎研究所，1986:1-33

［9］矢島浩.船殼の脆性破壞管理制御に関する基礎的研究［D］.東京:東京大學，1980.

［10］WES3003低溫鋼板判定基準［S］.東京:日本焊接協會出版，1995.