基于混凝土無應力計測值統計模型反演熱膨脹系數
唐騰飛,黃耀英,周宜紅,周紹武,李金河,景 繼,程中凱
(1.三峽大學水利與環境學院,湖北 宜昌 443002;2.中國長江三峽集團公司,湖北 宜昌 443002)
0 引 言
對于混凝土而言,溫度變形是材料熱脹冷縮引起的變形;濕度應變是混凝土因濕度變化而引起的變形;自生體積應變是由于水泥水化熱和其他一些未知的物理化學變化引起的,其變化規律比較復雜。溫度變形、濕度變形和自生體積變形都是自由體積變形,在實際混凝土工程上,一般采用無應力計來監測[1-2]。對無應力計測值進行分析時,一般選取降溫時段的無應力計測值的變化量和溫度測值的變化量來獲得熱膨脹系數,然后再分離出自生體積變形。由于自生體積變形變化規律比較復雜,有些混凝土工程的自生體積變形需要較長時間才能趨于穩定,這導致采用不同的降溫時段反演獲得的熱膨脹系數具有較大的差異,甚至是采用同一降溫時段,如采用中冷、二冷期間不同的降溫過程線,反演獲得的熱膨脹系數也具有一定的波動性。熱膨脹系數的差異直接導致分離的自生體積變形的不合理性。
大壩監測數據受到多種因素的復雜影響并存在監測誤差,具有不確定性,可看作是隨機變量。采用數值統計法定量處理這些數據,建立大壩監測統計模型來揭示測值的變化規律是一種常用的方法[3-4]。由于無應力計測值由溫度分量、自生體積變形和濕度變形等組成,通過建立無應力計測值的統計模型分離出溫度分量和自生體積變形分量,無疑是一條較好的途徑。本文探討基于無應力計測值統計模型反演混凝土熱膨脹系數以及分離自生體積變形分量。
1 混凝土熱膨脹系數反演分析的基本原理
1.1 傳統方法反演熱膨脹系數
熱膨脹系數可采用無應力測值反演獲得。通過無應力計實測的自由應變可用下式表示
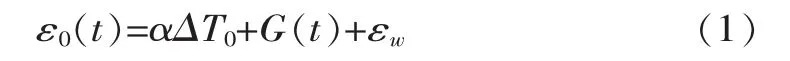
式中,αΔT0為溫度應變,α為熱膨脹系數;G(t)為自生體積變形;εw為濕度變形。
在一般情況下,混凝土的自生體積變形發生在早齡期,經過一段時間以后,變形將趨于平緩[5]。大體積混凝土內的濕度變化不大,由此認為,混凝土溫度開始下降時,濕度變形變化不大。即認為混凝土內部溫度下降時,有G(t)+εw≈0。此時,可以利用降溫時段的無應力計的應變測值和溫度測值來求得熱膨脹系數。在實際分析時,常在混凝土的降溫段取若干個無應力測值和相應溫度值,采用最小二乘法來求得熱膨脹系數。求得熱膨脹系數后,將無應力計測值扣除溫度分量,即可獲得自生體積變形分量。
1.2 基于無應力計測值統計模型反演熱膨脹系數
由混凝土自生體積變形的試驗資料可知,一般初期自生體積變形變化大,隨后呈單調遞減趨勢。參考朱伯芳院士提出的混凝土熱學力學性能隨齡期變化的組合指數公式[6],本文采用3個指數公式累加來描述自生體積變形的變化規律。對于溫度變形分量,則采用無應力計的溫度作為因子,而大體積混凝土內的濕度變化不大,不另選因子,由此建立無應力計測值統計模型為
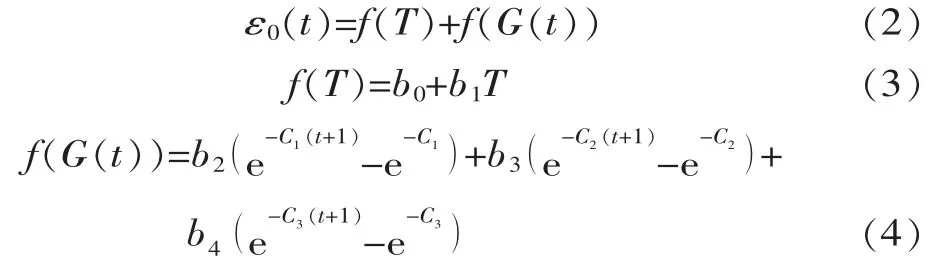
式中, f(T)為溫度分量; f(G(t))為自生體積變形分量; bi(i=0,4)為回歸系數; Ci(i=1,3)為常數, 根據回歸經驗,C1=0.3,C2=0.05,C3=0.005。
采用逐步回歸分析法獲得無應力計測值的統計模型回歸系數后,自動分離出溫度變形分量和自生體積變形分量,對比公式(2)和公式(1),可以認為系數b1即為熱膨脹系數,即b1=α。
2 工程應用
2.1 工程實例
某建設中的水電站混凝土高拱壩位于四川省雷波縣和云南省永善縣接壤的金沙江峽谷段,是一座以發電為主,兼有攔沙、防洪和改善下游航運等綜合效益的大型水電站。工程樞紐主要由攔河壩、泄洪、引水、發電等建筑物組成。攔河大壩為混凝土雙曲拱壩,壩頂高程610 m,最大壩高285.5 m。左、右兩岸布置地下廠房,各安裝9臺水輪發電機組,電站總裝機1 386萬kW,多年平均發電量571.2億kW·h。大壩共31個壩段。為對大壩混凝土的應力應變進行監測,在壩體混凝土內埋設了無應力計和應變計組進行監測。
由于該高拱壩混凝土自生體積變形較大,一般為收縮形,且穩定時間較長,本文分別采用傳統方法和無應力計測值統計模型反演熱膨脹系數,以下選取典型無應力計NCP14-1和NZ18-3X進行分析。基于無應力計統計模型反演熱膨脹系數時的回歸系數見表1;2種方法反演的熱膨脹系數見表2。實測值和擬合值對比見圖1;分離自生體積變形對比分析見圖2。另外,本文總共選取了15支無應力計,反演的熱膨脹系數和分離出來的自生體積變形的穩定值見表3。
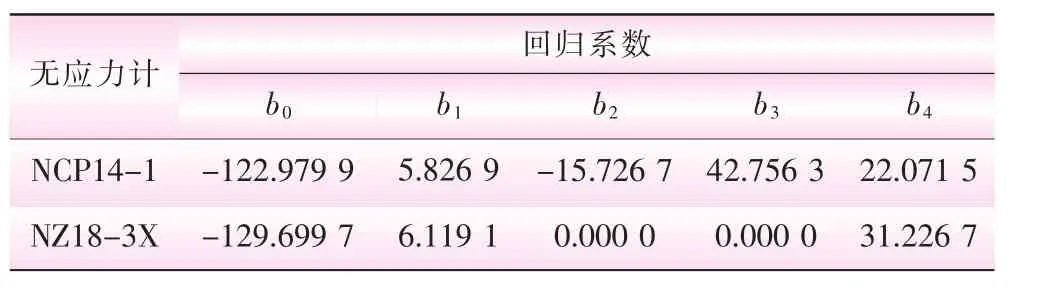
表1 統計模型回歸系數
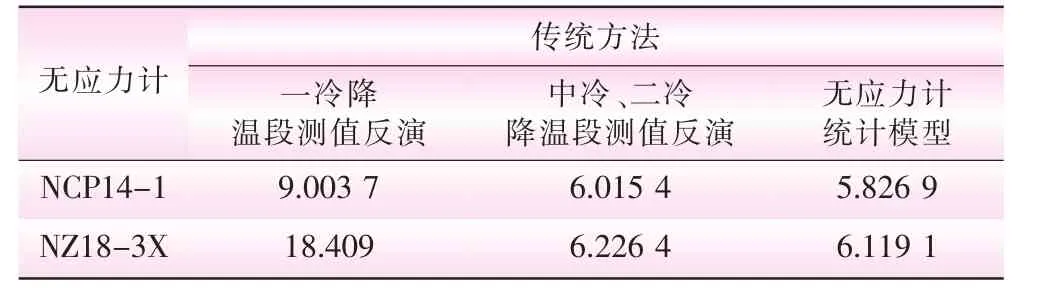
表2 典型無應力計反演熱膨脹系數對比10-6℃
2.2 成果分析
(1)典型無應力計擬合值和實測值吻合效果良好,如無應力計NCP14-1的復相關系數為0.992,無應力計NZ18-3X的復相關系數為0.989,這說明本文建立的無應力計測值統計模型是可行的。
(2)由表2可見,采用傳統方法反演混凝土熱膨脹系數,選取的降溫時段不同,反演得到的熱膨脹系數差異較大。分析還表明,即使采用中冷和二冷降溫期間的不同降溫段,反演的熱膨脹系數也存在一定的差異。而采用無應力計測值的統計模型反演的熱膨脹系數相對穩定,反演的熱膨脹系數綜合反映了整個溫度歷程,反演的值更可靠。
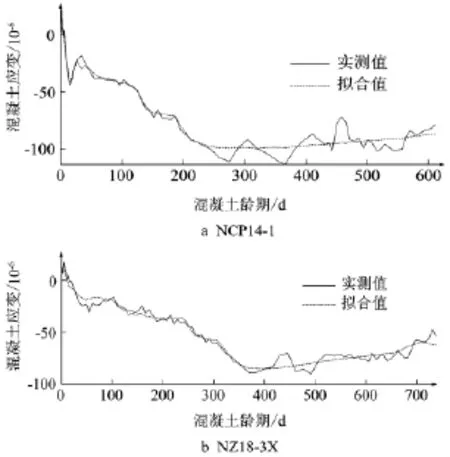
圖1 典型無應力計實測值與擬合值對比
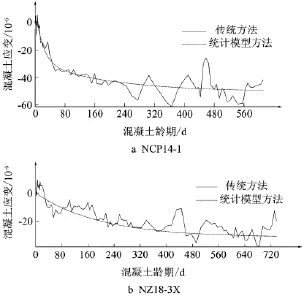
圖2 典型無應力計分離出的自生體積變形計算值與擬合值對比
(3)由表3可見,基于無應力計統計模型分離出的自生體積變形平均值隨時間逐漸趨于穩定,自生體積變形呈收縮形,穩定值的平均值大約為-40×10-6;反演的熱膨脹系數為4.863 3×10-6~7.704 2×10-6℃, 熱膨脹系數平均值為6.394 8×10-6℃。
3 結 語
(1)如果混凝土自生體積變形較大,且穩定時間較長,導致采用不同降溫時段無應力計測值反演的熱膨脹系數波動較大。
(2)建立了無應力計測值的統計模型,提出了基于無應力計測值統計模型反演混凝土熱膨脹系數,以及分離自生體積變形分量。實踐表明,該方法反演的混凝土熱膨脹系數穩定性較好。
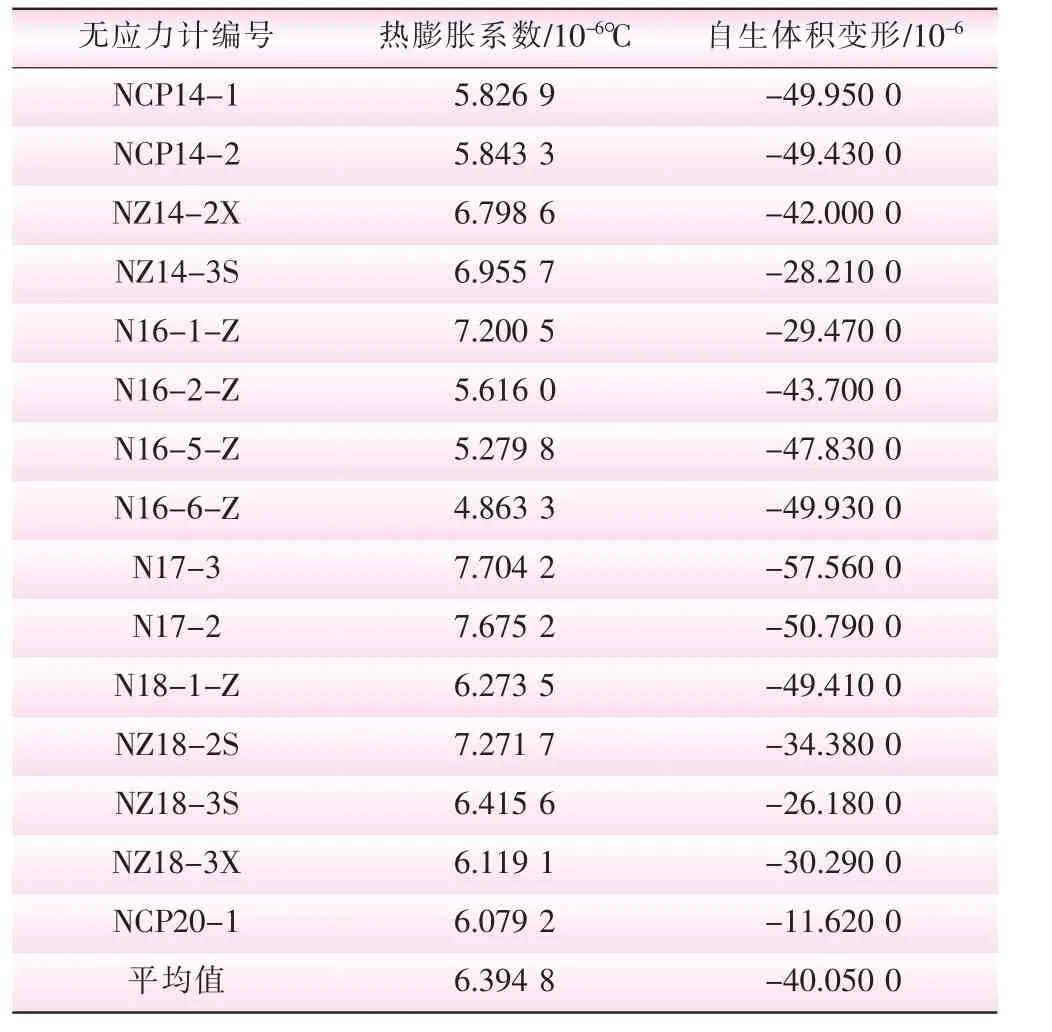
表3 反演的熱膨脹系數和分離自生體積變形穩定值
(3)結合某建設中的高拱壩的無應力計測值,采用本文提出的無應力計測值統計模型反演的混凝土熱膨脹系數平均值為6.394 8×10-6℃,自生體積變形呈收縮形,穩定值大約為-40×10-6με。
[1]吳中如.水工建筑物安全監控理論及其應用[M].北京:高等教育出版社,2003.
[2]儲海寧.混凝土壩內部觀測技術[M].北京:水利電力出版社,1989.
[3]李珍照.大壩安全監測[M].北京:中國電力出版社,1997.
[4]吳世勇,陳建康,鄧建輝.水電工程安全監測與管理[M].北京:中國水利水電出版社,2009.
[5]朱伯芳,張超然.高拱壩結構安全關鍵技術研究[M].北京:中國水利水電出版社,2010.
[6]朱伯芳.混凝土熱學力學性能隨齡期變化的組合指數公式[J].水利學報, 2011, 42(1):1-7.

