例談由具體到抽象原則在近世代數教學中的應用
張桂穎,李武明
(通化師范學院數學學院,吉林通化 134002)
近世代數也叫抽象代數,這門課程是數學與應用數學專業必開的一門重要的基礎課,而且對于以后攻讀代數學方向碩士研究生的學生來說,近世代數功底的深厚也直接影響著他們今后的學習情況.對于我們這類院校的學生來說,近世代數具有嚴密的邏輯性和特有的抽象性,學生很難學透,即使像群、子群、環、子環這樣的基本概念,學生要想真正掌握也非常吃力.許多學生對近世代數產生了畏難甚至厭惡情緒,再加上學時有限,要想讓學生在這有限的學時內較好的掌握近世代數的內容要領,在講課方法上必須仔細揣摩.
實際上對于大學的數學課都適合運用由具體到抽象原則的講課方法,尤其對于抽象的近世代數課程,在講解定義、定理時更應采用這種方法.所謂由具體到抽象的原則是指先舉出具體實例,由具體實例得出性質、結論,進而猜想抽象到一般情況是否成立,再利用邏輯推演證明其正確性,若能按照這樣的思路來處理每一個問題,勢必會使學生感覺到近世代數也不是那么難,也是有例可尋的.在近世代數中一個常被我們做引例而學生又比較熟悉的群就是三元對稱群,本文將以有限群論中Sylow定理的探求為例介紹由具體到抽象的原則,再簡要介紹這一原則在群的同態定理中的應用方式[1].
1 Sylow定理的探求
三元對稱群S3={(1),(12),(13),(23),(123),(132)}.
例1A3={(1),(123),(132)},A3是S3的正規子群,商群S3/A3={A3,(12)A3},|S3|=6=3×2,觀察發現有關于這三個群的一個命題.
命題1A3是S3的正規子群,則|S3|=|A3|·|S3/A3|
思考:用一般有限群G去替換特殊有限群S3命題是否仍然成立.由此提出如下猜想.
猜想1 若H是G的正規子群,則|G|=|H|·|G||G/H|.
結論是肯定的.由此還可以進一步驗證若m|n,|G|=n,G中是否存在階為m的子群H?這對有限交換群的確是成立的,可用于證明Sylow第一定理.
例2S3的共軛類劃分S3=C(1)∪C(12)∪C(123),即為S3的共軛類的不交并,其中
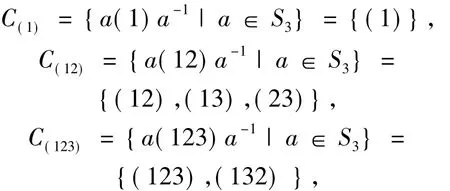
于是|S3|=6=1+3+2,觀察發現命題2.
命題2S3的共軛類劃分為S3=C(1)∪C(12)∪C(123),則
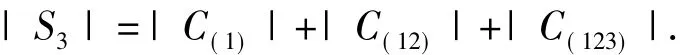
其中,C(1)是S3的中心,C(12)、C(123)中元素均大于1個.將這個等式抽象到一般有限群G便可得到類方程.
引理1[2]有限群G的中心C的元素個數c0,別的共軛類(如果存在,每類中元素的個數都大于1)設為C1,C2,…,Cm,且|Ci|=ci,i=1,2,…,m,于是有限群G的類方程|G|=c0+c1+…+cm.
注:類方程可應用于證明Sylow第一定理.
例3S3的共軛類劃分S3=C(1)∪C(12)∪C(123),進一步考察共軛類中元素的正規化子,得到
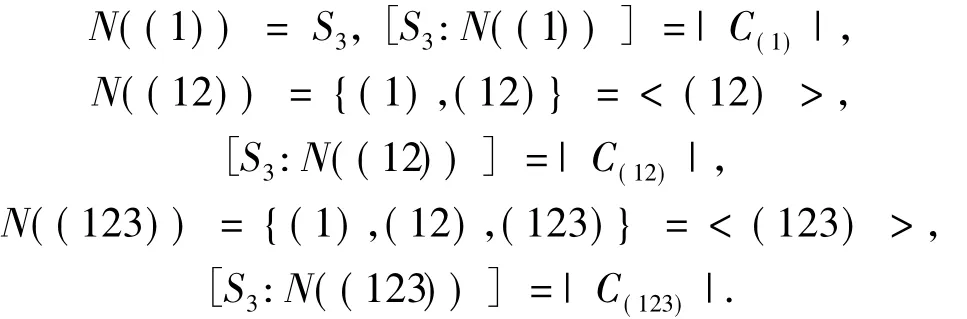
由此可得到關于特殊群S3的一個命題.
命題3a∈CaS3,有[S3:N(a)]=|Ga|.
進一步考慮用一般有限群G去替換特殊有限群S3命題是否仍然成立.
猜想2a∈CaG,有[G:N(a)]=|Ca|,其中,G為任一有限群,Ga為元素a的共軛類.
結論當然是肯定的,即為[1]中的引理7.10,結論可用于證明Sylow第一定理.
例4 考察三元對稱群S3的子群N((12))={(1),(12)}=<(12)>的共軛子群類
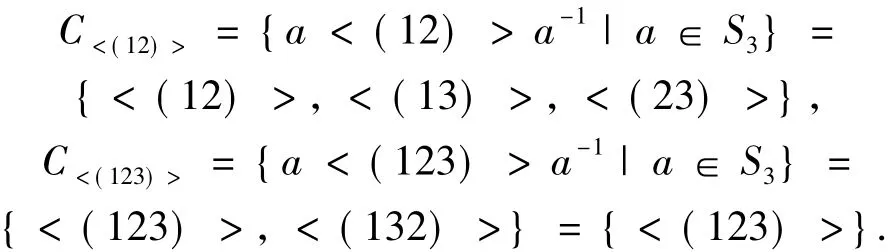
命題4 有限群S3的P(素數)階子群是相互共軛的.
猜想3 有限群G的P(素數)階子群是相互共軛的.
經討論猜想3有肯定的回答,結論可用于證明Sylow第二定理.有了以上的這些理論作為基礎,對于Sylow定理的證明便可迎刃而解.
2 群的同態定理的探求
保持運算的同態映射把群G中所有運算關系(指涉及元素和運算的所有等式)都傳遞給G的同態象.所以保持著G中的某些結構.群G的同態象可以設想為群G的一個“粗略”的模型:忽略了G中某些元素之間差異而又維持G中的運算關系.群的第一同態定理說群G的所有可能的“粗略”模型就是群G的那些商群;群的第二同態定理說明了群與它商群的子群之間的關系.
例5 群(Ζ,+)與群(C12,·)之間存在同態映射 φ:a|→ρaθ,其中C12={ρaθ|θ=,a∈Ζ}={ρaθ|0≤a≤11},群(G12,·)=Imφ={φ(a)|a∈Ζ},Kerφ={12t|t∈Ζ}=<12>是群 (Ζ,+)的正規子群,我們會發現商群Ζ/Kerφ≌Imφ,其中映射為a+k|→ φ(a).
由此我們可以抽象出群的第一同態定理.
例6 進一步對于群(Ζ,+)的幾個包含<12>=Kerφ的子群,有如下關系:<12>≤<6>≤<3>≤<1>=Ζ,其相應的象有<ρ0θ>≤<ρ6θ>≤<ρ3θ>≤<ρθ>,而且還保持一種正規性,比如:<ρ3θ><ρθ><3><1>,并且在這個條件下有關系<ρθ>/<ρ3θ>≌<1>/<3>.由此我們可以抽象出群的第二同態定理.
3 結語
總之,由具體到抽象的這一教學方法不僅可以使學生很好的學習近世代數知識,有效培養學生的思維,同時也可以使學生掌握這樣一種學習大學數學的通用方法,對他們以后的學習受益匪淺.對于近世代數這門比較抽象的理論課程,其教學方法是值得我們數學工作者進一步研究的.
:
[1]劉紹學.近世代數基礎[M].北京:高等教育出版社,1999.
[2]楊子胥.近世代數[M].第2版.北京:高等教育出版社,2003.
[3]張禾瑞.近世代數基礎[M].北京:人民教育出版社,1978.
[4]顧沛.抽象代數教學中的素質教育[J].大學數學,2006,22(3):9 -13.
[5]夏靜波,鄒庭榮,張四蘭.近世代數的教學技巧[J].大學數學,2009,25(1):5 -8.

