兩種色散特異材料雙層結構中的法諾共振機制

劉艷紅，劉麗想，董麗娟，石云龍

（山西大同大學固體物理研究所，山西大同 037009）

兩種色散特異材料雙層結構中的法諾共振機制

劉艷紅，劉麗想，董麗娟，石云龍

（山西大同大學固體物理研究所，山西大同 037009）

單負特異材料雙層結構中，由于分離式的反射共振和寬帶的強反射之間發生的法諾型干涉，在反射譜中出現了非對稱法諾譜。當光斜入射到單負特異材料異質結時，分離式的反射共振發生在單負特異材料色散磁導率接近于零的頻率點。通過解析和數值分析得到，法諾型反射的非對稱因子與入射角是密切相關的。

單負特異材料；法諾共振；法諾因子

1 引言

近年來，法諾共振機制吸引了人們大量的關注，在原子、大體積固體和半導體異構體系的光譜中普遍存在。法諾線性不同于傳統的對稱共振曲線，其最初起源于原子的吸收譜，原子中的各種電子組態分為分立能態和連續能態，正是這種連續態與分立態間的相互作用導致其吸收譜呈現一個不對稱的峰形［1］。利用子能帶間躍遷的法諾干涉可以實現隧穿透明［2，3］。由于法諾共振原理圖像比較簡單，所以可以將其拓展到其它許多系統中。如果將法諾共振類比到光物理中，法諾型共振其實就是由一對競爭的光通道之間的量子力學共振或干涉所產生的一種光譜失真效應，也就是共振吸收和共振發射同時共存的效應。它反映了離散的能量狀態是怎樣與其環境中的連續狀態耦合在一起的。在非線性體系中，法諾干涉的可見度急劇增加，這可被用作關于離散狀態和連續狀態之間耦合程度的一種靈敏探針［4］，利用非線性法諾體系還可以實現的光開關，而且透射比可以達到100％［5］。因此研究各種系統的法諾共振是非常有意義的事情。

自從在原子系統中發現法諾共振后，人們在其它許多物理系統中也發現了法諾型非對稱譜線。特別是，在經典系統法諾共振的實現引起了人們的關注。2002年，范三慧研究小組在一個二維光子晶體波導的一側耦合一個微腔的系統中發現了非對稱法諾共振的現象［6］。之后，許多種法諾型共振在各種各樣的光子晶體體系被找到。此外，在一些納米系統包括等離子體納米結構［7］或者特異材料［8］中觀察到法諾共振現象。例如，在周期性金屬結構或者金屬薄板上對稱刻痕的系統中也存在法諾共振效應。

法諾線性不同于傳統的對稱共振曲線，是由于較窄的分立譜線和較寬的譜線或者是連續譜相互干涉相消和干涉相長同時存在的非對稱譜線。美國物理學家Ugo Fano在他最初的文章中推導出法諾共振的簡單表達式如下：

其中，Ω表示一個無量綱的頻率，是由分立態的中心頻率譜線寬度決定的。q表示法諾非對稱參數，是由混合態的躍遷幾率和連續態的躍遷幾率之比決定的，它描述的是譜線非對稱程度的大小。文獻［9］中給出了法諾共振的譜線的形狀，如圖1所示。

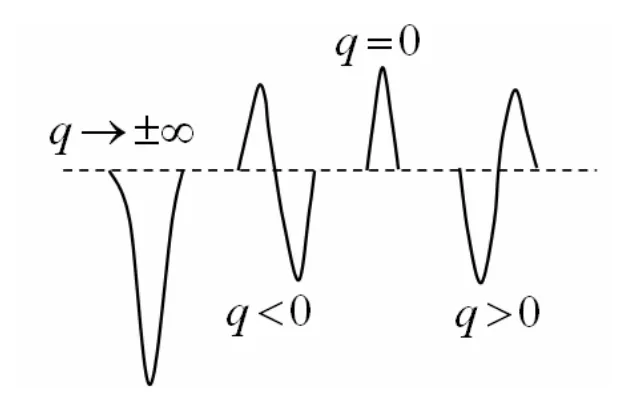
圖1 可能出現的法諾線性譜

本文研究特異材料中的另一種類型的法諾共振。色散型特異材料雙層結構是由電單負特異材料（介電常數為負值，磁導率為正值）［10］和磁單負特異材料（介電常數為正值，磁導率為負值）［11］組成的。在可見光頻段，金屬在其等離子頻率以下是天然的電單負特異材料［12］。對于磁單負特異材料，雖然自然界不存在，但是可以通過由非磁性的導體共振單元組成的平面結構來實現［13］。我們知道，對于電單負和磁單負單層結構，電磁波是不透的，其中電磁波只能以倏矢波的形式存在。然而，在2003年A.Alù課題組發現對于電單負和磁單負構成雙層結構，當滿足阻抗和相位匹配的條件，電磁波能夠共振隧穿通過單負異質結［14］。2007年，該課題組又研究了介電常數接近于零的特異材料及等離子材料對電磁波的影響，他們給出的平面波反射系數（公式2）的表達式中可以看到，對于橫磁（TM）極化平面波對于單層介電常數為零的板層結構是不透的，除非入射平面波精確正入射［15］。

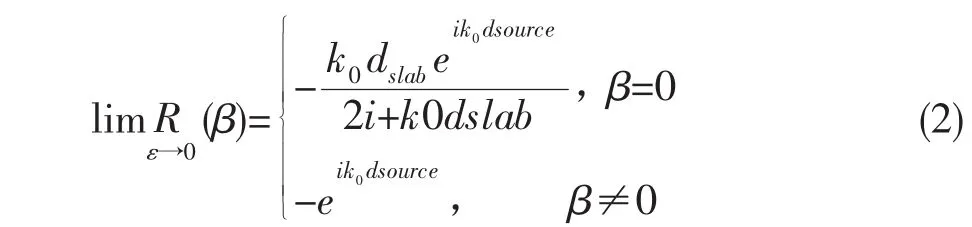
其中，β＝sinθ，θi為平面波的入射角。

可見，對于色散型電單負和磁單負組成的雙層結構，且工作頻率段內包含磁單負特異材料的磁導率等于零的頻率點時，電磁波的傳輸是非同尋常的。

2 法諾型非對稱反射譜的計算

在圖2中，給出了對于TE和TM模式的電磁波在電單負和磁單負雙層結構中的法諾共振機制圖，其中圖2（a）中是電單負和磁單負雙層結構圖，圖2（b）中給出了當電磁波入射到電單負和磁單負組成的雙層結構時，可能發生的兩種反射路徑。

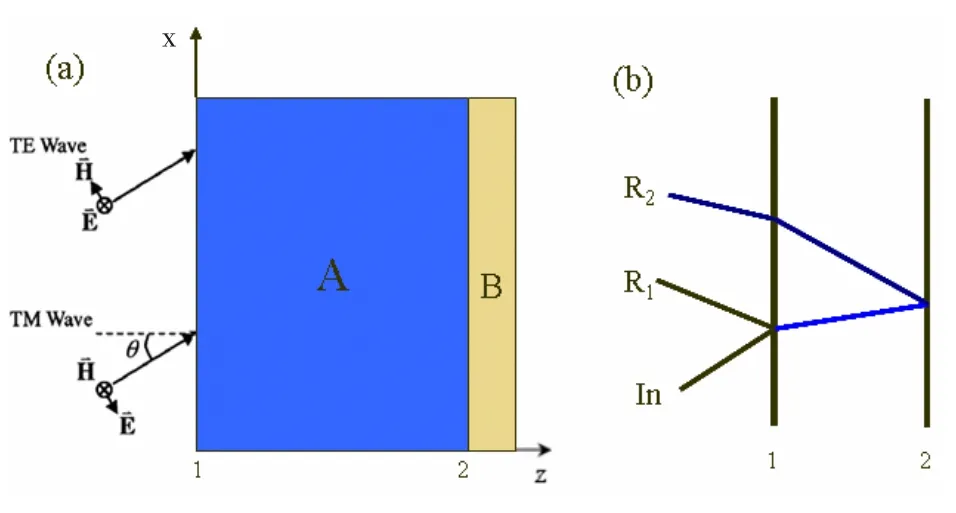
圖2 法諾共振系統結構圖

從圖中可以看到，一種是發生在入射界面的反射，它是較寬帶的反射，可以被看作是背景反射譜或者是連續譜；另一種是先入射到單負A然后經過兩個單負的界面反射后，再經過入射面被反射出來，當頻率為單負介質的介電常數或者磁導率接近于零的條件，且電磁波斜入射時這種反射譜是較窄帶的反射可以被看作是分立譜。在下面的計算中我們令A層為電單負層，B層為磁單負層，且只考慮TE極化波為入射波。根據二相性原理，對于TM極化波我們只要將A層和B層分別換為磁單負層和電單負層即可的得到與TE極化波相似的結果，所以我們不做考慮。

假定電單負特異材料的相對介電常數為εENG和相對磁導率為μENG，厚度為a。磁單負特異材料的相對介電常數為εENG和相對磁導率為μENG，厚度為b。對于電單負材料的相對介電常數和磁單負材料的相對磁導率用德魯得模型來表示，

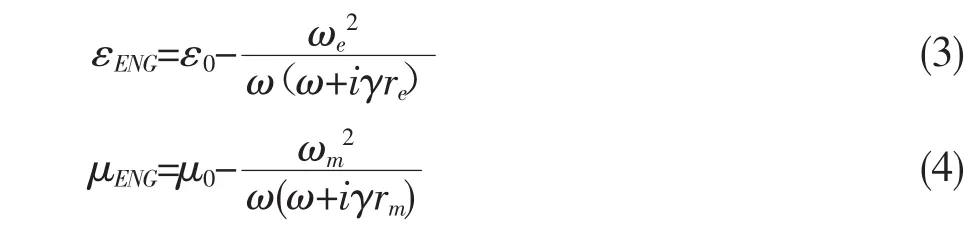
其中ωe和ωm分別表示電和磁的等離子體頻率，γ表示損耗系數。

首先通過傳輸矩陣的方法計算了單層單負材料的反射譜。在以下的計算中，我們選擇兩種單負材料的電場參數為，

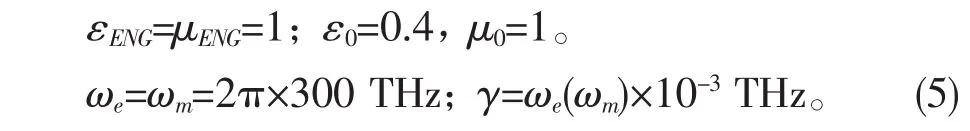
這樣由式（4）我們可以得到，當入射頻率達到磁單負材料的磁等離子頻率（300THz）時其色散磁導率接近于零（μENG→0）。在圖3，中我們給出了入射角分別為π/18，2π/9和4π/9時的單層單負結構的反射譜。圖3（a）中，可以看到對于電單負單層在頻率范圍為250THz時的反射譜是寬帶的反射譜，這是因為電單負材料是不透明的不支持導模，所以其表面上光的發射可以被看作是強的連續反射譜。而對于磁單負單層結構在以上頻率范圍內的斜角度入射時的反射譜，見圖3（b），是較窄帶的。雖然正入射時在此等離子頻率點光是沒有反射的，但是，當光波斜入射到磁單負材料時由于其表面在此等離子頻率點的全反射（由阻抗強烈不匹配引起），導致了反射譜中出現了非常尖銳的反射峰，這樣，如果將磁單負的材料參數設計到除了等離子頻率點以外的其它點的反射較小，就可得到品質因子Q很高的反射譜。高Q反射譜可以看作是分立譜，而且從圖3（b）中還可以看到，Q的大小是與光波的入射角有關的。

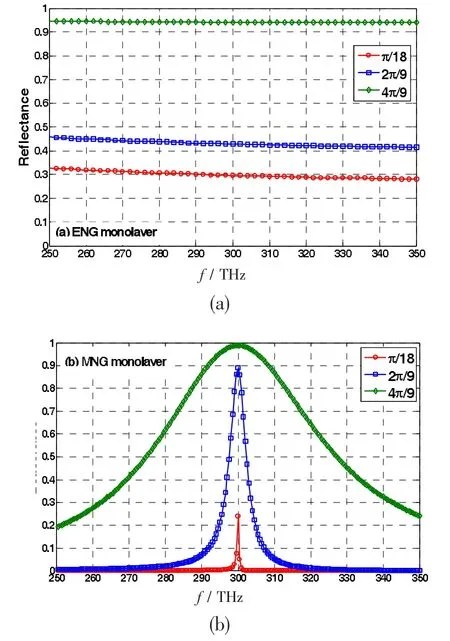
圖3 單層單負結構反射譜

當光波斜入射到由電單負和磁單負構成的雙層結構時，首先會在電單負層的入射界面被部分反射，形成比較強的連續的反射譜。同時，穿透電單負層的光波將被近鄰的磁單負層反射，在磁單負的相對磁導率接近于零的頻率點，形成窄的分立的反射共振峰。下面具體計算這兩種反射路徑相互作用形成的法諾型非對稱反射譜。選擇的電單負和磁單負材料的厚度分別a＝120nm和b＝10nm。當磁單負的損耗系數較小時，可以認為，磁導率等于零的頻率點為f＝ωm/2π＝300THz。

通過傳輸矩陣法推導分析由電單負和磁單負材料構成的雙層結構的反系數的表達式。對于TE模式的光波經過單負雙層結構的反射系數的表達式為：

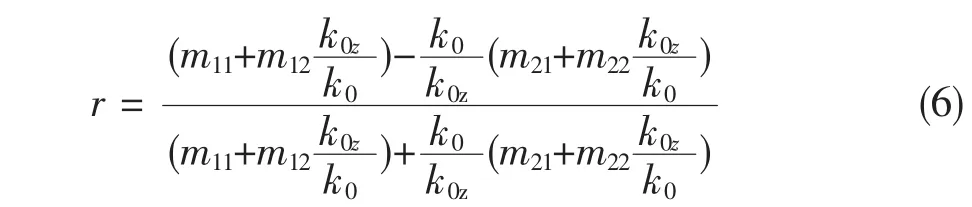
其中，mi，j（i，j＝1，2）為光波經過雙層單負材料的傳輸矩陣的矩陣元，

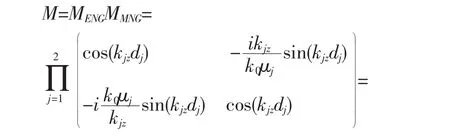
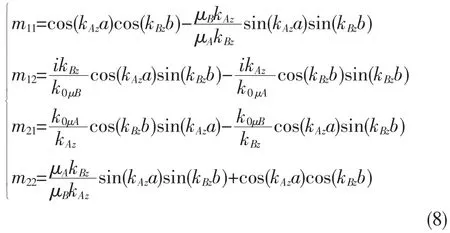
其中，A表示電單負材料，B表示磁單負材料。因為我們選擇的單負材料的結構長度遠小于波長，所以可以近似認為|kAz|a＝1，|kBz|b＝1，這樣，可以圍繞|kjz|dj進行以下的Taylor近似展開。

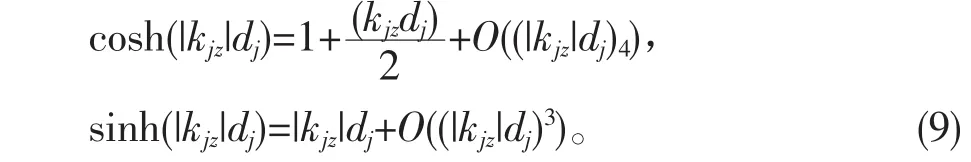
由于表達式比較冗長，所以將一些常量用簡單的字母代替表示，假定電單負材料的相對介電常數為εA＝-α（α＞0），當磁單負材料的相對磁導率接近于零時，我們將式（6）近似寫作：

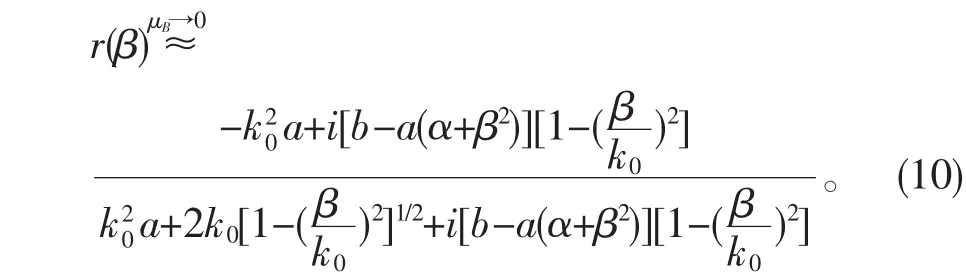
這樣，就可以計算反射率R為：

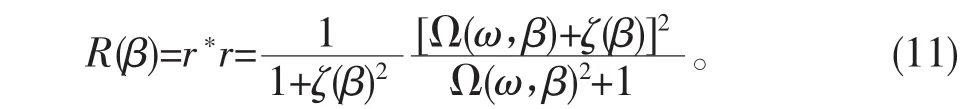
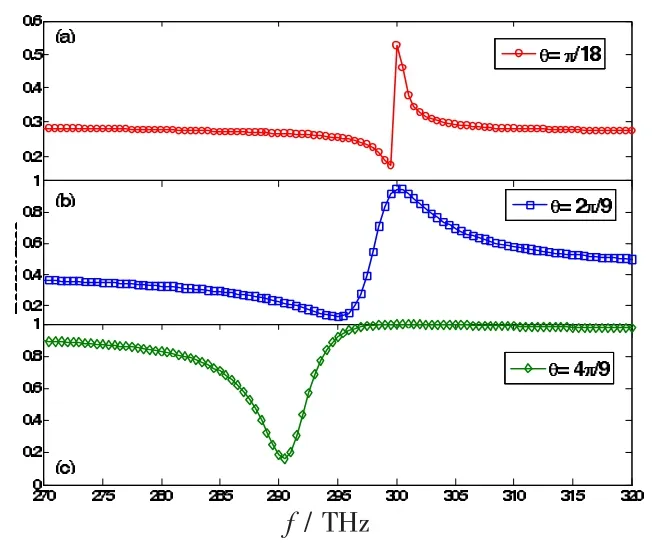
圖4 TE模式的電單負和磁單負雙層結構的不同入射角度的反射譜

通過公式（11），理解法諾散射的機制，在公式中的變量函數ζ（β）對應于表征法諾振動非對稱程度的非對稱參數q，而且隨著平行方向傳播常數β的增大，其數值是增加的。變量函數Ω（ω，β）也是β的函數。圖4中從上到下的三幅圖中，可以看到對稱性反射譜的形狀強烈依賴于入射角。在我們計算的入射角范圍為π蛐18-4π蛐9內，隨著入射角的增大β值的增大，導致了對稱參數q值的增大，我們找到了與圖1中對應的變化趨勢，隨著法諾因子的增加，反射譜由反射峰變化到對稱反射譜的低谷。我們還計算了透射譜，見圖5。

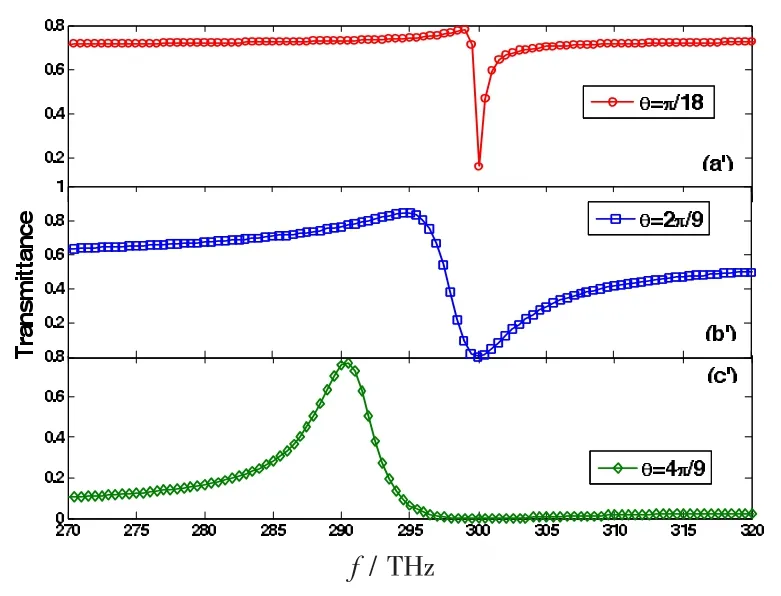
圖5 TE模式的電單負和磁單負雙層結構的不同入射角度的透射譜

從圖5中可以看到，由于計算過程中選取了小的損耗系數所以得到了非對稱的透射譜。最后，我們還計算了圖4（a）中的反射谷的頻率（299.5THz）處的電磁場強度的分布，假定入射場的強度為1，計算結果見圖6。從圖6中會發現，比較奇特的事情是在磁單負層內的局域的磁場的幅值相比較于入射場的近42倍。下面分析一下物理原因，對于TE模式的電磁波，磁感應強度的縱向分量Bz＝μHz，要滿足邊界條件中的連續性。當μ值趨于零時，使得界面兩側的材料的磁導率有嚴重的區別，所以磁場強度的z分量就會在邊界處有巨大的跳躍變化。如果磁單負材料具有克爾型非線性，那么磁場強度z分量的很強的增大會很好的促進非線性效應，更有利于實現光學雙穩態。

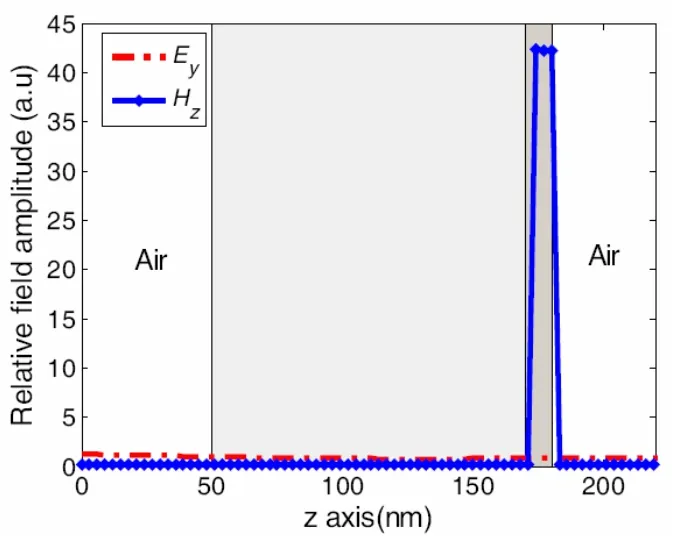
圖6 在2.995THz點單負雙層結構中的電磁場布圖

3 結論

通過與原子系統的類比，我們證明了，在色散型單負特異材料雙層結構中，由于分離式的反射共振和寬帶的強反射之間發生的法諾型干涉，在反射譜中出現了非對稱法諾譜。當光斜入射到單負特異材料異質結時，分離式的反射共振發生在單負特異材料色散磁導率接近于零的頻率點。通過解析和數值分析得到，法諾型反射的非對稱因子與入射角是密切相關的。在量子系統中，原子能級間的躍遷和退級是不能調節的，而在雙層單負特異材料系統中，對應的參量可以通過改變結構常數和入射角進行系統的調節，從而方便地研究這些參量對法諾共振現象的影響。另外，當磁單負特異材料的磁導率趨于零時，在磁單負特異材料里的局域磁場振幅會增強到入射場的42倍。這樣如果磁單負特異材料具有克爾型非線性，將會促進光學雙穩態的實現，而且使得非線性法諾共振現象變得更容易。

［1］Fano U.Effects of configuration interaction on intensities and phase shifts［J］.Phys Rev，1961，124：1866-1878.

［2］Faist J，Sirtori C，Capasso F，et al.Tunable Fano interference in intersubband absorption［J］.Opt Lett，1996，21（13）：985-987.

［3］Schmidt H，Campman K L，Gossard A C，et al.Tunneling induced transparency：Fano interference in intersubband transitions［J］.Appl Phys Lett，1997，70：3455.

［4］Kroner1 M，Govorov A O，Remi S，et al.The nonlinear Fano effect［J］.Nature，2008，451：311.

［5］Mingaleev S F，Miroshnichenko A E，Kivshar Yu S.Coupled-resonator-induced reflection in photonic crystal waveguide structures ［J］.Opt Express，2008，16：11647-11659.

［6］Fan S H.Sharp asymmetric line shapes in side-coupled waveguide-cavity systems［J］.Appl Phys Lett，2002，80：908-910.

［7］Hao F.Symmetry breaking in plasmonic nanocavities：Subradiant LSPR sensing and a tunable Fano resonance［J］.Nano Lett，2008，8：3983-3988.

［8］luk′yanchuk1 B，nikolay I Z，stefan A M，et al.the Fano resonance in plasmonic nanostructures and metamaterials［J］.Nature Materials，2010，9：707-715.

［9］Rybin M V，Khanikaev A B，InoueM，et al.Bragg scattering induces Fano resonance in photonic crystals［J］.Photonics and Nanostructures-Fundamentals and Applications，2010，8：86-93.

［10］Pendry J B，Holden A J，Stewart W J，et al.Extremely low frequency plasmons in metallic mesostructures［J］.Phys Rev Lett，1996，76（25）：4773-4776.

［11］Zhang S，Fan W J，Minhas B K，et al.Midinfrared resonant magnetic nanostructures exhibiting a negative permeability［J］.Phys Rev Lett，2005，94（3）：037402.

［12］Moerland R J，van Hulst N F，Gersen H，et al.Probing the negative permittivity perfect lens at optical frequencies using near-field optics and single moleculedetection［J］.Opt Express，2005，13：1604-1614.

［13］Yen T J，Padilla W J，Fang N，et al.Terahertz magnetic response from artificial materials［J］.Science，2004，303：1494-1496.

［14］Alù A，Engheta N.Pairing an epsilon-negative slab with a mu-negative slab：Resonance，tunneling and transparency［J］.IEEE Trans Antennas Propagat，2003，51，2558-2571.

［15］Alù A，Silveirinha M G，Salandrino A，et al.Epsilon-near-zero metamaterials and electromagnetic sources：Tailoring the radiation phase pattern［J］.Phys Rev B，2007，75：155410.

〔責任編輯 李海〕

Fano Resonances in a Bilayer Structure Composed of two Kinds of Dispersive Metamaterials

LIU Yan-hong，LIU Li-xiang，DONG Li-juan，SHI Yun-long
（Institute of Solid State Physics，Shanxi Datong University，Datong Shanxi，037009）

We theoretically find that a bi-layer structure composed of two kinds ofdispersive metamaterials can possess an asymmetric reflection spectrum due toFano-type interference between a discrete reflection resonance and a broadbandstrong reflection.The discrete reflection resonance appears at the frequency around which the dispersive permeability is near to zero at oblique incidence.Based onanalytical and numerical analysis，the asymmetric factor in the Fano-type reflection is found to be linked with the angle of incidence.

single negative metamaterial；Fano resonance；Fano paremeter

O571.5

A

1674-0874（2012）05-0021-05

2012-05-25

山西省教育廳高校高科技項目［20111119］

劉艷紅（1979-），女，山西文水人，博士，講師，研究方向：凝聚態物理。