逐點比較直線插補算法的優化

楊 威，應保勝，邱新橋，吳岳敏

（1.武漢科技大學機械自動化學院，湖北武漢，430081；2.湖北汽車工業學院機械工程系，湖北十堰，442002）

逐點比較直線插補算法的優化

楊 威1，應保勝1，邱新橋2，吳岳敏1

（1.武漢科技大學機械自動化學院，湖北武漢，430081；2.湖北汽車工業學院機械工程系，湖北十堰，442002）

基于八方向插補算法，提出一種改進的逐點比較插補算法。通過最大插補誤差分析，利用解析求解、數值比較及計算機運算，得到一種插補精度較高、運算速度較快、速率較平穩的偏差計算方法。

數控系統；逐點比較插補法；直線插補；優化改進

插補運算是計算機數控（Computer Numerical Control，CNC）系統中生成加工軌跡的一個基本子程序，它直接影響到工件的輪廓精度、表面光滑度和機床的最大進給速度［1－3］。插補算法分為基準脈沖插補算法和數據采樣插補算法。基準脈沖插補算法中最常用的是逐點比較法。逐點比較法的優點是算法簡單、插補計算速度快、插補誤差較小，但同時也存在如下缺點：①不能兩軸聯動，影響加工精度；②插補次數多，執行時間長，影響生產效率［4］。

本文在逐點比較法的基礎上，改變判斷點的取值，增加一個進給方向，以圖進一步提高插補精度和運算速度。

1 插補原理

逐點比較法的基本原理［5］為：計算機在控制加工軌跡的過程中，刀具每進一步（一個脈沖當量）都將實際加工點同規定的軌跡進行比較，并計算一次偏差值，從而決定下一進給點，以逼近給定的軌跡。因此刀具每進給一步都要經過如下4個節拍：偏差計算、位置判別、坐標進給、終點判別。

2 改進算法的插補方法與實現過程

逐點比較插補算法只有＋x、＋y、－x、－y四個進給方向，八方向插補算法［6］是在該四個進給方向上再增加＋x＋y、－x＋y、－x－y、＋x－y四個進給方向。其中，＋x＋y是指＋x和＋y坐標方向同時進給，其余類推。八方向插補算法進給方向如圖1所示。

圖1 八方向插補算法進給方向Fig.1 Coordinates of eight directions interpolation algorithm

2.1 證明插補直線與任意插補點的位置關系

圖2 任意加工起點時插補直線通過區域Fig.2 Interpolation curve at any starting point of processing

設任意直線AB為加工軌跡，則刀具瞬時加工點p0（xi，yi）在任意位置都有3個進給方向（見圖2），下一進給點是p′1、p″1、p?1中的某一點。點A與插補起點p0重合，此時直線AB通過正方形區域p0p′1p″1p?1，證明插補i次后，直線AB通過區域pip′i＋1p″i＋1p?i＋1。證明：

（1）在插補起點時，直線AB通過正方形區域p0p′1p″1p?1；

（2）插補i次后，插補點為pi（xi，yi），直線AB通過正方形區域pip′i＋1p″i＋1p?i＋1；

（3）第i＋1次插補有3個插補點p′i＋1（xi＋1，yi）、p″i＋1（xi＋1，yi＋1）、p?i＋1（xi，yi＋1），分別為如下3種情形：①第i＋1次插補點為p′i＋1（見圖3），直線AB通過p′i＋1p′i＋2p″i＋2p?i＋2；②第i＋1次插補點為p″i＋1（見圖4），直線AB通過p″i＋1p′i＋2p″i＋2p?i＋2；③第i＋1次插補點為p?i＋1（見圖5），直線AB通過p?i＋1p′i＋2p″i＋2p?i＋2。

可見上述假設成立。證畢。

圖3 插補點為p′i＋1時插補直線通過區域Fig.3 Interpolation line at the interpolated point p′i＋1

圖4 插補點為p″i＋1時插補直線通過區域Fig.4 Interpolation line at the interpolated point p″i＋1

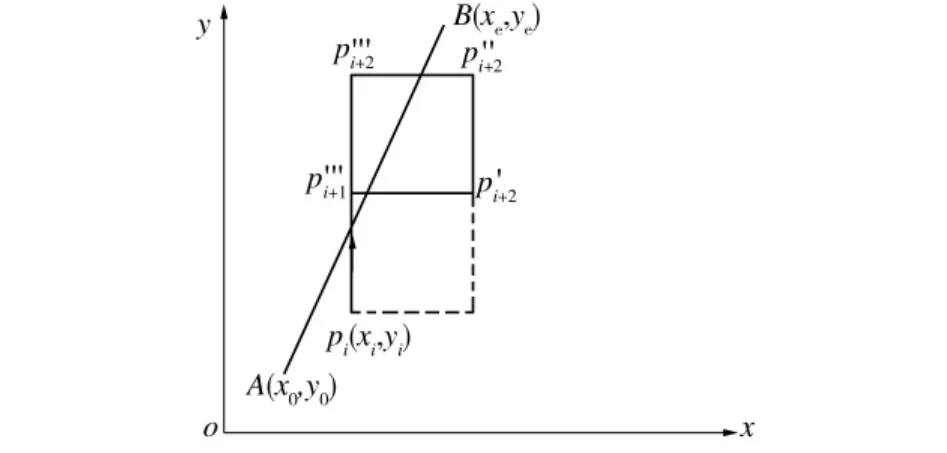
圖5 插補點為p?i＋1時插補直線通過區域Fig.5 Interpolation line at the interpolated point p?i＋1

2.2 最大誤差臨界角計算

任意直線AB為加工軌跡，刀具瞬時加工點pi（xi，yi）在任意位置都有3個進給方向（見圖6）。下一進給點是p′i＋1（xi＋1，yi）、p″i＋1（xi＋1，yi＋1）或p?i＋1（xi，yi－1）中的某一點。根據2.1的證明，直線AB總是通過區域pip′i＋1p″i＋1p?i＋1。分別作p′i＋1L、p″i＋1N垂直于直線AB，垂足為L、N。點M為直線AB與直線p′i＋1p″i＋1的交點。則，當下一進給點為p′i＋1時，誤差為p′i＋1L；當下一步進給點為p″i＋1時，誤差為p″i＋1N。從圖6中可看出，顯然點p?i＋1不可能成為最小誤差插補點，因此只需在p′i＋1L與p″i＋1N中選擇。

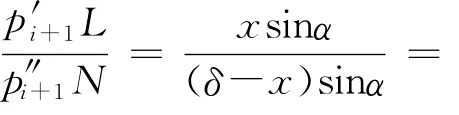
圖6 M點在p′i＋1p″i＋1上時最大誤差臨界角Fig.6 Maximal critical angle of error at point M for middle point of p′i＋1p″i＋1

圖7 M點為p″i＋1p?i＋1中點時最大誤差臨界角Fig.7 Maximal critical angle of error at point M for middle point of p″i＋1p?i＋1

2.3 最大誤差計算

2.4 偏差計算

偏差計算以第Ⅰ象限的直線為例（見圖8、圖9）。設直線的起點為o（0，0），終點為B（xe，ye），其他點定義同圖6。當xe＝0時，刀具沿x軸方向進給；當ye＝0時，刀具沿y軸方向進給；當xe≠0且ye≠0時，交點為M1、M2、M3、M4，顯然，延長線上的交點M2和M4應被排除掉。

點M1坐標可由下式確定：

圖8 M點在p′i＋1p″i＋1上時的偏差Fig.8 Error at point M for middle point of p′i＋1p″i＋1

圖9 M點在p″i＋1p?i＋1上時的偏差Fig.9 Error at point M for middle point of p″i＋1p?i＋1

2.5 偏差判別

2.5.1 長度比較法

如圖8、圖9所示：

當β∈［arctan0.5，90°－arctan0.5）時，Fij＝2；

當β∈［90°－arctan0.5，90°）時，Fij＝3。

2.6 坐標進給

當Fij＝1時，下一個插補點選擇點p′i＋1；

當Fij＝2時，下一個插補點選擇點p″i＋1；

當Fij＝3時，下一個插補點選擇點p?i＋1。

2.7 終點判別

起點為（x0，y0）（一般取為原點（0，0）），終點為（xe，ye）的直線，其判別值（直線在x、y軸方向上的總步長）為Im，則：Im＝xe－x0＋ye－y0。

2.8 不同象限的插補分析

對于任意象限的直線插補，可以先通過坐標平移將起點移至坐標原點，再根據直線終點的所在象限，應用坐標變換方法，將其變換為標準的第一象限內直線來插補。直線插補坐標變換法如表1所示，其中U表示x軸方向進給，V表示y方向進給。

表1 直線插補坐標變換法Table 1 Coordinate synopsis of linear interpolation

3 結語

改進后的逐點比較直線插補算法通過改變判斷點的取值，增加了一個插補運動方向，其插補誤差僅為傳統算法誤差的1／2，插補次數相應減少，從而提高了插補精度和加工速度。

［1］ 王愛玲.現代數控原理及控制系統［M］.北京：國防工業出版社，2002.

［2］ 張建剛，胡大澤.數控技術［M］.武漢：華中科技大學出版社，2000.

［3］ 李佳.數控技術及應用［M］.北京：清華大學出版社，2001.

［4］ 張柱銀，姚建明，李碩.數控系統中逐點比較法的優化算法［J］.機械研究與應用，2010，23（1）：42－44.

［5］ 蘇秀平.細論直線的逐點比較法插補［J］.機床與液壓，2004（4）：119－121.

［6］ 范希營，郭永環.數控系統基準脈沖插補的發展方向［J］.機床與液壓，2010，38（20）：109－111.

Optimization of point－by－point comparison linear interpolation algorithm

Yang Wei1，Ying Baosheng1，Qiu Xinqiao2，Wu Yuemin1
（1.College of Machinery and Automation，Wuhan University of Science and Technology，Wuhan 430081，China；2.Department of Mechanical Engineering，Hubei University of Automotive Technology，Shiyan 442002，China）

Based on the eight directions interpolation algorithm，an improved point－by－point comparison interpolation algorithm was proposed.By maximum interpolation error analysis，analytical solution，numerical comparison，and computer computation，an error calculation method was obtained，which boasts higher interpolation precision，stable computation，and higher computation speed.

NC system；point－by－point comparison interpolating algorithm；linear interpolation；optimization

TB115

A

1674－3644（2012）03－0222－04

［責任編輯 彭金旺］

2011－10－25

楊 威（1989－），男，武漢科技大學碩士生.E－mail：710327911＠qq.com

應保勝（1964－），男，武漢科技大學教授，博士生導師.E－mail：635125316＠qq.com