豎向地震作用下橋梁結構的瞬態(tài)波響應分析
徐 然,尹曉春
(1.南京理工大學 力學與工程科學系,南京 210094;2.常州大學機械學院力學系,常州 213016)
近年來淺源近斷層地震動的觀測記錄顯示,豎向地震動與水平地震動分量的比值往往大于我國工程抗震設計規(guī)范中通常采用的2/3,而且出現(xiàn)了大幅值的豎向地震動加速度[1-3]。1994年發(fā)生在美國的 Northbridge地震,豎向加速度峰值高達1.18 g,是水平加速度峰值的1.79倍[1],如此高的豎向地震動引起了極大的關注,因此成為豎向地震動研究的分水嶺。在1995年的Kobe地震中,觀測到的地面豎向加速度峰值高達水平值的兩倍[2]。2008年發(fā)生在我國的汶川地震中,豎向地震動加速度峰值達到1g[3],接近于水平加速度峰值。調查工程結構在豎向地震作用下的損壞發(fā)現(xiàn),豎向地震動可能造成與水平地震動不同的損壞現(xiàn)象,如出現(xiàn)樓層整體壓潰、墻體豎向夾角小于橫向夾角的“X”型裂縫、受拉破壞的水平環(huán)縫、鋼筋“燈籠狀”壓曲等特殊現(xiàn)象[1,4]。因此,被低估的豎向地震動對工程結構可能造成的損害,受到了越來越多的關注。
有關的研究顯示,豎向地震動循環(huán)往復的地震力可能在橋梁的混凝土橋墩中產生巨大的應力,甚至喪失豎向承載能力,引起橋梁倒塌[5-6]。另一方面,支座與橋跨結構之間的接觸力可能因豎向地震的作用而減小[7],造成橋梁和橋墩之間的摩擦力減弱,使得落橋等震害更容易發(fā)生。豎向地震動產生的向上的拉力作用于支座上時,可引起橋梁與支座連接構件的拉斷或者支座斷裂等,也可能引起支座和上部結構發(fā)生暫時的分離,引發(fā)上跳現(xiàn)象[8]。Tanimura 等[9]假設橋跨發(fā)生了跳起后的再次落下撞擊,采用動力學有限元方法模擬了下部結構的損壞情況,模擬結果與實際發(fā)生的損壞情況基本一致。
對于橋梁在水平地震分量激勵下的地震響應時程分析,目前一般采用的研究方法有兩種:其一是將橋梁簡化為“梁-桿”模型,對耦合地震力(位移)的控制方程應用差分法求其數(shù)值解;其二是建立橋梁的有限元模型進行計算[10-13]。這兩種計算方法均沒有考慮結構的波動效應。針對豎向地震分量激勵下的橋梁地震響應,需要將橋跨結構按梁結構,橋墩按桿結構考慮,從而建立“梁-桿”連續(xù)體模型。可以采用瞬態(tài)波特征法進行理論求解和分析,以得到豎向地震波傳播過程中的橋梁響應。
本文應用彈性動力學理論中的瞬態(tài)波特征函數(shù)法,研究雙跨連續(xù)梁橋在豎向地震動激勵下的瞬態(tài)波傳播問題。通過選取不同的豎向地震動與水平地震動的比值,對比研究橋墩和橋跨結構響應的變化。計算結果表明,該方法可以描述出地震激勵產生的瞬態(tài)波的反射、相互作用和波碰撞等波傳播現(xiàn)象,合理模擬豎向地震作用下的橋梁的動力學行為,求解復雜的地震激勵下的結構瞬態(tài)波響應問題。
1 結構模型
本節(jié)針對一雙跨連續(xù)梁橋(圖1)闡述研究方法,研究該橋梁在豎向地震激勵作用下的瞬態(tài)動力學響應。設橋跨結構參數(shù)為:跨長x0=50 m,橫截面面積A=11.3 m2,截面慣性矩 I=22.7 m4;材料為 C50 混凝土:彈性模量 E=34.5 GPa,密度 ρ=2 500 kg/m3;橋墩結構參數(shù)為:墩高L=20 m,橫截面面積Ar=15 m2;鋼筋混凝土橋墩采用C20標號的混凝土:彈性模量Ec=30 GPa,密度ρc=2 500 kg/m3。橋墩縱向配筋為II級鋼筋,直徑40 mm,基本間距為100 mm,保護層厚度為50 mm,沿截面四周均勻布置,配筋率為1.3%。箍筋同樣為II級鋼筋,直徑16 mm。鋼筋的抗拉(壓)設計強度fy=300 MPa,彈性模量為Ey=200 GPa。
由于橋墩中的混凝土和縱筋的彈性模量不一致,根據(jù)橋墩截面變形一致性假設,可以計算出橋墩的等效彈性模量Er=(EcAc+EyAy)/(Ac+Ay),橋墩的等效應力σr為軸力除以橋墩橫截面面積,其中Ac為截面混凝土面積,Ay為全部縱向鋼筋的截面面積。
橋跨結構與橋墩之間的支座采用型號為XQZ6000的球型支座,該鋼支座的彈性模量Ez=206 GPa,密度ρz=7 850 kg/m3,橫截面面積 Az=0.51 ×0.51 m2,高度H=135 mm,在豎直方向y上沒有位移約束。根據(jù)圖1模型,可以計算出XQZ6000的球型支座承受的靜接觸力F0=17.27 MN,在該靜載作用下,在球型支座各結構件壓實的條件下,可以近似按照均質彈性體計算出支座的靜變形量Δδ為:
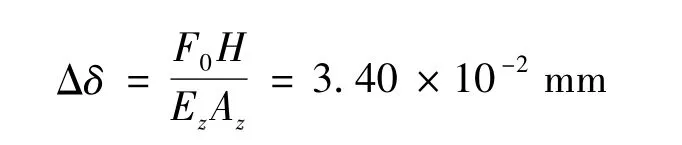
它是橋墩靜載變形量ΔL:
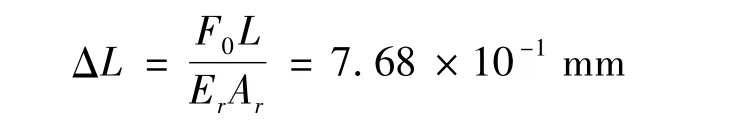
的4.43%。另外,彈性應力波在橋墩中傳播時間tr為:
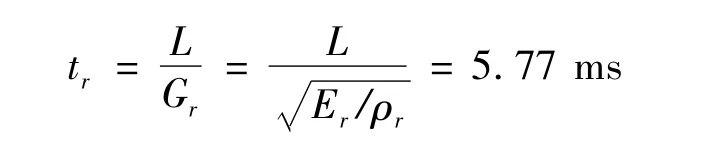
遠遠大于穿過支座需要的時間tz:
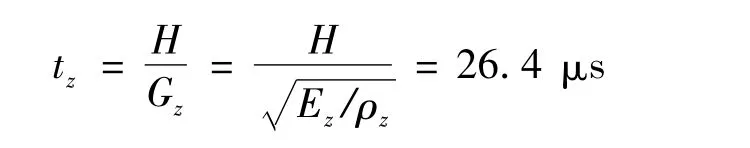
上述比較表明,支座的變形和波傳播效應對于該雙跨連續(xù)梁橋豎向地震響應的影響可以忽略。因此,在圖1的模型中,不考慮支座的作用。
將豎向地震激勵簡化為簡諧運動,以地震主要周期作為激勵周期T,選取地震持續(xù)時間為10 s。對于復雜的豎向地震波動響應,可以通過FFT方法將其分解為各級簡諧地震激勵,然后利用簡諧豎向地震激勵的研究結果,采用疊加法加以分析。
對于圖1所示的連續(xù)梁橋模型,不考慮支座的作用,將橋跨結構簡化為梁Ω1,橋墩簡化為桿Ω2,梁兩端界面為ΓA和ΓB,梁和桿的接觸界面為ΓC,桿下端的固支界面為ΓD。將梁的自重作為均布外載q施加在梁上,豎向地震激勵的作用等效為基礎運動B(t),并取豎向地震波到達的時刻為計算的零時刻。
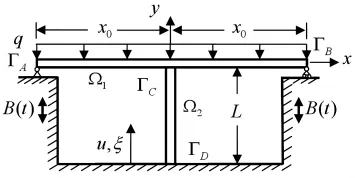
圖1 雙跨連續(xù)梁橋模型Fig.1 Model of two-span continuous bridge
2 瞬態(tài)波響應理論解
2.1 波動方程
橋跨結構采用Bernoulli-Euler梁模型,橋墩采用St.Venant桿模型。應用彈性動力學理論,得到梁Ω1和桿Ω2的波動方程為:
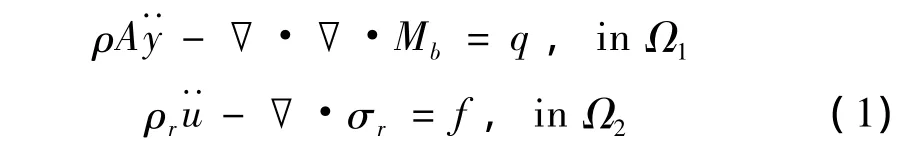
其中,y和u分別為梁的撓度和桿的軸向位移,Mb為梁的彎矩,σr為桿的軸向應力,不計橋墩體力時f=0。在豎向地震作用下,橋梁結構的邊界條件為:
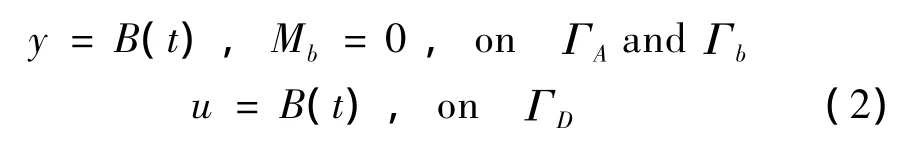
接觸界面ΓC的位移連續(xù)性條件和力連續(xù)性條件為:
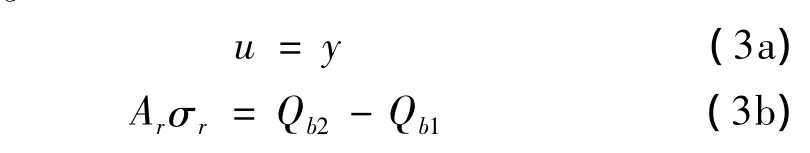
其中,Qb1和Qb2分別為從左端和右端計算的梁中部的剪力。初始條件為:
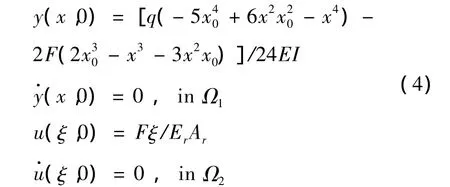
2.2 瞬態(tài)波函數(shù)解
應用瞬態(tài)波特征函數(shù)法對偏微分方程組(1)進行求解[14~16]。將梁-墩位移分布分解為準靜態(tài)項和動態(tài)項兩部分:
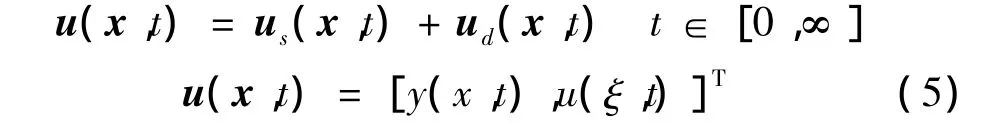
其中,準靜態(tài)解應滿足平衡微分方程、真實的邊界條件(2)和連續(xù)性條件(3)。動態(tài)解應滿足波動方程(無載荷q)、連續(xù)性條件(3)、初始條件(4)和齊次邊界條件
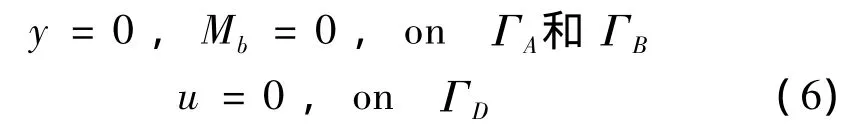
最終使解(5)滿足波動方程、邊界條件、連續(xù)性條件和初始條件。根據(jù)彈性動力學解的唯一性定理,可以得到圖1雙跨連續(xù)梁橋模型的瞬態(tài)波響應的精確理論解。
按照上面所述方法,解得橋梁結構的準靜態(tài)項us(x,t)為:
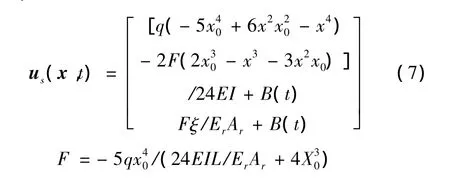
在豎向地震響應過程中,梁和桿以共同的特征頻率ωn運動,動態(tài)位移項可表示成如下形式
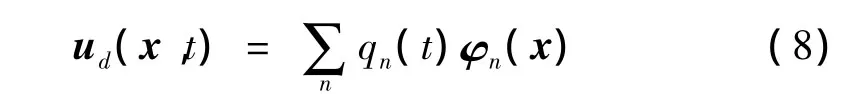
其中,梁和桿的波模態(tài)函數(shù) φn(x)= [φbn,φm]T滿足特征方程:
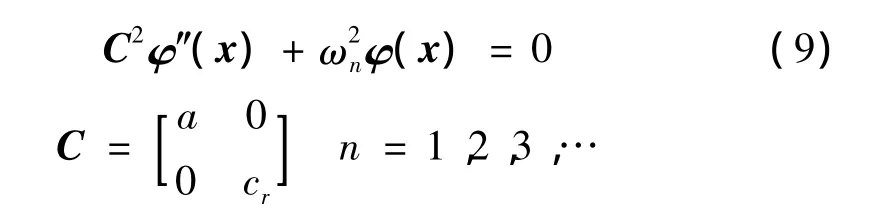
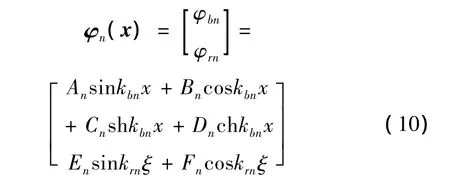
其中,kn=[kbn,krn]TBn,Cn,Dn,En,F(xiàn)n]T為待定系數(shù)。由齊次邊界條件列出關于待定系數(shù)的線性方程組,根據(jù)非平凡解存在的條件,即的系數(shù)矩陣行列式為零,導出頻率方程為:
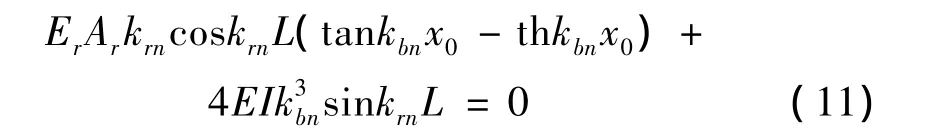

將位移解(5)代入波動方程(1),并應用正交性條件,可導出時間函數(shù)的微分方程為:
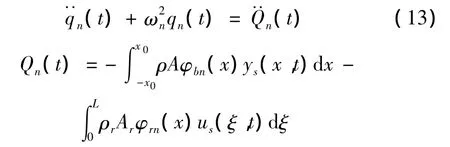
采用Laplace變換求解可得:
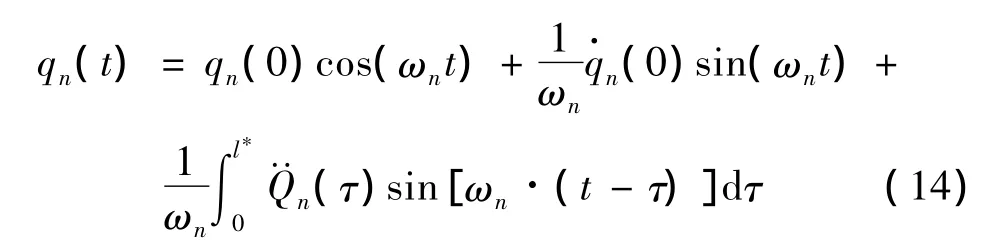
其中,qn(0)和n(0)由地震開始時刻梁和桿的位移和速度分布所確定。
利用公式(5)求出橋梁整體結構的瞬態(tài)響應解后,可由接觸界面上的應力計算出橋跨結構與橋墩之間的接觸力P(t),計算公式為:

2.3 橋跨結構發(fā)生跳起時橋梁響應的計算
陳興沖等[8]的研究表明,當豎向地震的拉力大于接觸面承受的壓力時,橋跨結構將發(fā)生上跳。在整個地震過程中,反復循環(huán)的地震荷載可能造成橋跨結構多次上跳。在本文中,采用文獻[17]中提出的計算多次重撞擊響應的方法,如果橋跨結構發(fā)生上跳,則將整個地震過程分割為交替出現(xiàn)的橋跨結構和橋墩的接觸過程和分離過程。由于接觸過程和分離過程是不同拓撲的結構,需要分開求解。
由接觸過程進入分離過程的條件為接觸力為零,即:

而由分離過程進入接觸過程的條件為梁和墩在接觸處的位移相等,即條件(3a)。
接觸過程的計算方法如公式(5)-(15)所述,所不同的是,式(14)中的qn(0)和n(0)是由上一次過程結束時梁和桿的位移和速度分布所確定的。下面主要闡述分離過程的計算方法。
在分離過程中,橋跨結構與橋墩各自獨立運動,應分別求解振動響應。其邊界條件為:
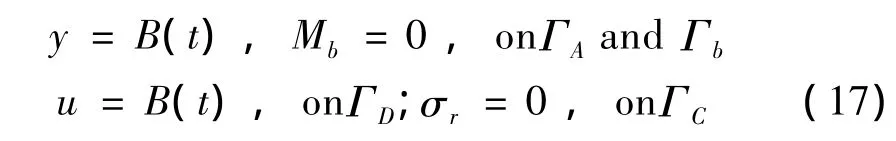
應用瞬態(tài)波特征函數(shù)法,解得獨立運動的梁和桿的準靜態(tài)項us(x,t)為:
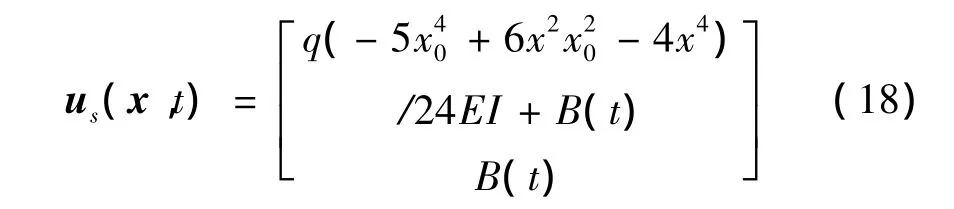
梁和桿的波模態(tài)函數(shù)分別為

由齊次邊界條件和正交性條件解得
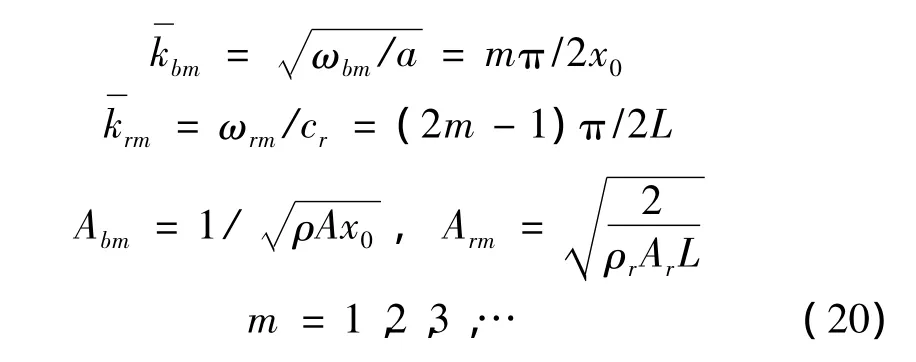
求解時間函數(shù)得:
其中,qbm(0),qrm(0),bm(0)和rm(0)由上次接觸階段結束時刻的位移和速度分布所確定。
3 豎向地震的瞬態(tài)波響應分析
3.1 豎向地震波在橋跨結構和橋墩中的傳播
選取豎向地震激勵周期T=0.1 s,橋梁所在地區(qū)抗震設防烈度為九度。按罕遇地震作用計算[18],地震波的水平加速度峰值為0.62 g,按照規(guī)范取豎向地震波的加速度峰值為水平峰值的2/3,即0.4 g。在豎向地震作用下,在橋跨結構中出現(xiàn)彌散形式的彎曲波,在橋墩中出現(xiàn)非彌散的軸向波。可采用無量綱化長度=ξ/L和=x/x0作為橫坐標,以軸力波表達軸向波,以動彎矩波(彎矩減去恒值的靜彎矩)表達彎曲波。
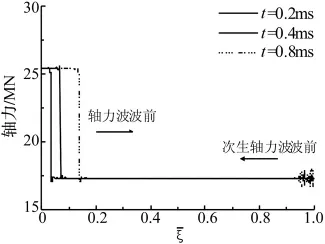
圖2 軸力波和次生軸力波的傳播Fig.2 Axial force wave and secondary axial force wave
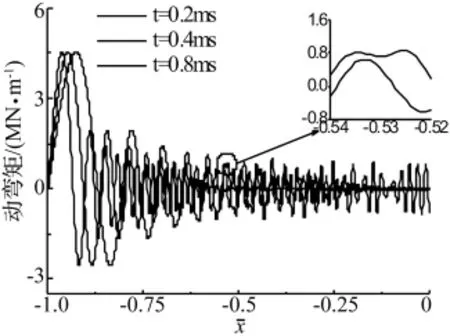
圖3 動彎矩波和次生動彎矩波的傳播Fig.3 Dynamics bending moment wave and its secondary wave
圖2和圖3的計算結果表明,當豎向地震在橋跨兩端和橋墩底部同時開始激勵,則動彎矩波從橋跨的兩端向中間傳播,軸力波從橋墩底部向頂部傳播。計算表明,動彎矩波先于軸力波傳播到橋跨的中部,時間大約在0.5 ms左右。此時,軸力波向上傳播了1.76 m。動彎矩波在傳播到中端后,將與橋墩相互作用,產生兩個新的波。一個是新的次生動彎矩波,向橋跨的兩端傳播,一個是次生軸向力波,向橋墩底部傳播。次生動彎矩波與從橋端傳播過來的動彎矩波相互作用,產生圖3中局部放大圖中所示的波干涉現(xiàn)象,使合成動彎矩波產生次振蕩。由于橋跨中端與橋墩是力相互作用方式,在橋墩中產生的次生軸力波是由彎曲剪力引起的,它是動彎矩波的導數(shù)形式,故振蕩比動彎矩波更加明顯。
在橋跨中產生的次生動彎矩波與豎向地震激發(fā)的動彎矩波相向而行,它在傳播到橋跨端部時會出現(xiàn)反射,然后向橋跨中部反向傳播,可引起上部結構動彎矩分布的更多振蕩。大約在t=3 ms時,橋墩中的軸力波與次生軸力波相碰撞,兩波發(fā)生相互作用,使得在軸力波波前之后的橋墩中產生高頻振蕩的軸力變化。但是,軸力波仍然在向橋墩頂傳播,并在t=5.77 ms時傳播到橋墩頂。
大約在t=5.77 ms時,軸向波傳播到橋墩頂,與彎曲波發(fā)生碰撞,產生了復雜的波動效應,圖4描述了波碰撞后產生的反射軸力波向橋墩底部傳播的過程。波碰撞的結果是在橋墩中產生了高幅值的碰撞軸力波,波峰幅值大約為原軸力波幅值的兩倍。碰撞軸力波的波形為:先突然上升,然后呈指數(shù)衰減,與一般的固體撞擊波形相似。碰撞軸力波的峰值近似為原先傳播的軸力波的兩倍,說明產生了應力加倍效應,該計算結果表明橋跨對于橋墩的約束效應類似于固定端約束效應。
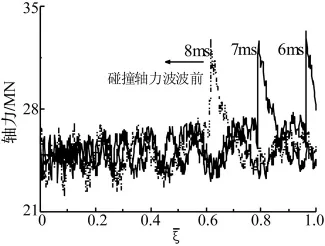
圖4 軸向撞擊波的傳播Fig.4 Impact axial force wave propagation
如圖5所示,軸向波與彎曲波發(fā)生的波碰撞同樣會在橋跨結構中產生向橋兩端傳播的碰撞彎矩波。碰撞的一個顯著結果是:在中部產生了一個高幅值的負的動彎矩,其幅值大約是原最大正動彎矩的兩倍。
當t=11.54 ms時,碰撞軸力波前波傳至橋墩底部,然后發(fā)生反射。當t=17.31 ms時,反射的碰撞軸力波傳至橋墩頂,與橋跨中的動彎矩波發(fā)生二次波撞擊,隨即產生二次碰撞軸力波,并從橋墩頂向橋墩底部傳播。當 t=17.31+11.54=28.85 ms時,產生了第三次碰撞軸力波。
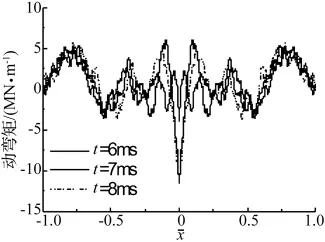
圖5 動彎矩撞擊波的傳播Fig.5 Impact dynamics bending moment wave propagation
以上的計算結果表明,本文方法可以計算豎向地震波在橋梁結構中的傳播,描述出地震激勵產生的瞬態(tài)波的反射、相互作用和波碰撞等波傳播現(xiàn)象,從而為合理計算橋梁在豎向地震激勵下的結構動態(tài)響應提供了理論基礎。
3.2 橋跨結構與橋墩的接觸力
在前面的計算中,取豎向地震分量與水平地震分量的比值β=2/3。但是,一些危害巨大的重要地震記錄顯示,豎向地震分量超過了該比值。尤其是在近場地震動記錄中,往往出現(xiàn)大幅值的豎向地震動。為此,本文專門選取β為1/2、2/3、1和3/2進行相應的計算分析,來對比研究豎向地震的影響。
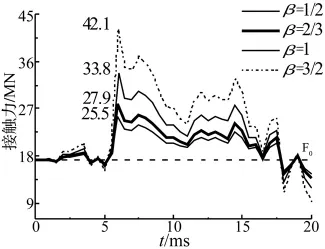
圖6 接觸力的變化Fig.6 Variations of contact force
圖6為地震開始后20 ms內不同β下的接觸力的變化情況,圖中標記的最大接觸力的數(shù)值隨β的增加近似于線性增加。在5.77 ms之前,接觸力在靜接觸力F0=17.27 MN基礎上作小幅振蕩。從5.77 ms開始,接觸力發(fā)生了顯著的變化,先是迅速上升,然后振蕩下行。由圖4可知,該急劇變化的接觸力是由于橋墩軸向波和橋跨彎曲波的第一次碰撞所造成的。
從圖7中地震開始后0.1 s內接觸力的變化情況看,在豎向地震波作用下,接觸力不僅會出現(xiàn)明顯超過靜接觸力F0的情況,也會出現(xiàn)明顯低于靜接觸力的情況。超過靜接觸力過多,會造成支座的損傷;接觸力過低,支座接觸面的水平摩擦力就會過小,當橋梁受到后繼橫向地震的共同作用時,橋跨結構滑動的可能性大大增加,從而可能導致落梁現(xiàn)象的發(fā)生。大約在β=1時,可能出現(xiàn)零接觸力現(xiàn)象,大大增加了落橋的可能性。
3.3 橋跨的跳起現(xiàn)象
圖7顯示,當β=3/2時,在0.1 s的響應時段內,出現(xiàn)三次接觸力為零的短暫時刻,原則上說明橋跨已經(jīng)與橋墩脫離接觸,可能發(fā)生了橋跨跳起現(xiàn)象,而該現(xiàn)象在β小于1的時候并沒有出現(xiàn)。
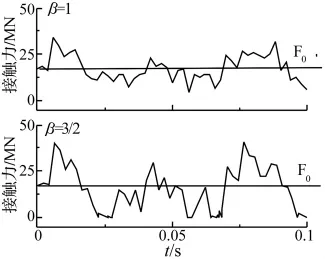
圖7 0.1 s內接觸力的變化Fig.7 Variations of contact force within 0.1 s
觀察圖8(a)可以發(fā)現(xiàn),當β=3/2時,在0.097 s~0.107 s時段內,橋跨與橋墩的相對分離位移量雖然只有0.056 mm,在實際過程是難以觀察到的,但是,出現(xiàn)了接觸力明顯偏低的一個時段,在該時段內橋跨滑動的可能性大大增加。圖8(b)顯示,在已考慮上部結構自重的情況下,分離時梁體相對橋墩的加速度大于零,也就是說地震引起的慣性力大于結構自重,所以橋跨結構將發(fā)生上跳。
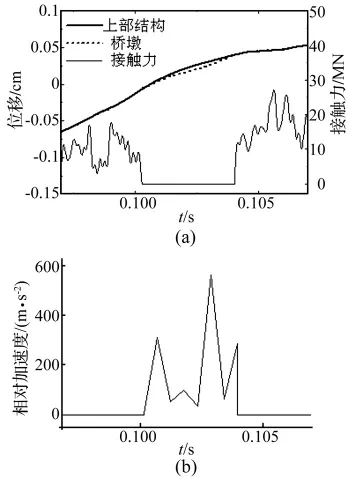
圖8 上部結構與橋墩之間的分離Fig.8 Separation between superstructure and pier
3.4 橋墩應力的變化
橋墩中原本保持一致的靜態(tài)壓應力,在豎向地震波作用下出現(xiàn)變化,甚至產生了拉應力截面。對于β=2/3情況,當t=0.816 s時,橋墩中的拉應力達到最大值。根據(jù)橋墩截面變形一致性假設,計算出此刻的混凝土的應力沿橋墩高度分布情況如圖9所示。
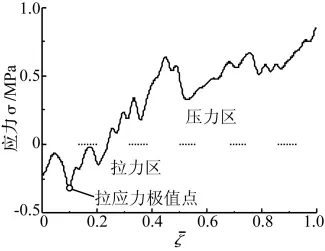
圖9 橋墩混凝土應力分布Fig.9 Distribution of axial stress of concrete
計算不同β取值下的橋墩混凝土的最大拉應力可以發(fā)現(xiàn),β的變化不僅會引起最大應力的變化,而且會引起響應特征的改變。當β=1/2時,橋墩中可以認為只有壓應力,也就是整個橋墩一直處于受壓狀態(tài),不會出現(xiàn)混凝土開裂的情況。而在其它β取值下,橋墩中出現(xiàn)了拉應力,整個橋墩出現(xiàn)了拉壓交變應力,橋墩的響應特征出現(xiàn)了明顯的改變。當β=3/2,即豎向加速度峰值為0.9 g時,最大拉應力為1.80 MPa,發(fā)生在橋墩底部,并且已超過了橋墩材料C20混凝土的抗拉強度1.54 MPa,可能導致混凝土開裂。
由于拉-壓應力交替出現(xiàn),可以認為橋墩可能出現(xiàn)多條裂縫,裂縫的間距可計算出為357.1mm。在整個地震作用過程中,拉應力會多次超過混凝土的拉伸強度,在拉-壓交變應力的循環(huán)作用下,可能造成更嚴重的破壞,出現(xiàn)橋墩底部混凝土破碎現(xiàn)象[1]。由此可見,對于處在豎向地震幅值較大的近斷層位置的橋梁,進行抗震設計時應將豎向地震分量對結構可能造成的損害考慮在內。
3.5 橋跨響應的變化
在不同β取值下,計算橋跨結構最大正彎矩Mmax和最大負彎矩Mmin。最大正彎矩出現(xiàn)在單跨偏橋端3/5處,最大負彎矩出現(xiàn)在橋梁中部。如圖10所示,最大正彎矩和最大負彎矩都隨β呈近似線性的增加。
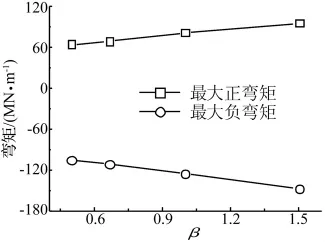
圖10 最大和最小彎矩隨β的變化Fig.10 Comparison of maximum and minimum bending moment in different β
另外,計算出的橋跨的最大動撓度(撓度減去初始時刻的靜撓度)分布曲線(圖11)表明,隨著β的增加,橋梁明顯上抬。當β>1后,橋跨中部向上的動撓度超過兩端,也就是橋跨結構被拋起的可能性增大。
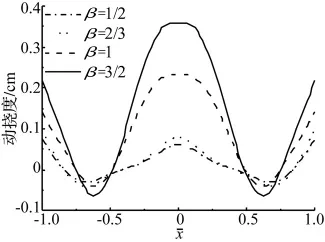
圖11 最大動撓度隨β的變化Fig.11 Comparison of maximum dynamic deflection in different β
4 結論
本文采用瞬態(tài)波特征函數(shù)法,考慮豎向地震作用下的波動效應,研究了雙跨連續(xù)梁橋在豎向地震激勵下的瞬態(tài)動力學響應。計算結果表明,本文方法可以計算豎向地震波在橋梁結構中的傳播,描述出地震激勵產生的瞬態(tài)波的反射、相互作用和波碰撞等波傳播現(xiàn)象。對于可能出現(xiàn)高幅值豎向地震加速度的近場地震,按照規(guī)范設定的豎向地震動與水平地震動分量的比值β=2/3來計算,可能低估最大接觸力,從而低估支座損壞的可能性;同樣也可能低估最小接觸力,從而低估橋跨與支座間出現(xiàn)滑動的可能性。通過選取不同的豎向地震動與水平地震動的比值β,對比研究了豎向地震可能對橋梁結構造成的影響。數(shù)值計算的結果表明:
(1)隨著β的增大,最大接觸力、橋跨結構最大正彎矩、最大負彎矩和最大動撓度近似線性增大。
(2)在不同的β下,橋墩對豎向地震的響應特征出現(xiàn)了本質性的變化。當β較大時,接觸力明顯偏低,大大增加橋跨滑動的可能性,并且可能出現(xiàn)了接觸力為零的短暫時刻,原則上說明橋跨與橋墩可能脫離接觸,有可能發(fā)生了橋跨跳起現(xiàn)象。
(3)隨著β的增大,原本處于受壓狀態(tài)的橋墩中出現(xiàn)了拉應力,甚至可能超過混凝土的抗拉強度,導致混凝土開裂。整個橋墩出現(xiàn)了拉壓交變應力,使橋墩底部處于危險應力狀態(tài)。
(4)在不同的β下,橋跨結構對豎向地震的響應特征也出現(xiàn)了明顯變化。當β較大時,橋跨中部向上的動撓度超過兩端,也就是橋跨結構被拋起的可能性增大。
[1]Papazoglou A J,Elnashai A S.Analytical and fileld evidence of the damaging effect of vertical earthquake ground motion[J]. Earthquake Engineering and Structural Dynamics,1996,25:1109-1137.
[2]Yang J,Lee C M.Characteristics of vertical and horizontal ground motions recorded during the Niigata-ken Chuetsu,Japan Earthquake of 23 October 2004 [J].Engineering Geology,2007,94:50-64.
[3]Wang D,Xie L L.Attenuation of peak ground accelerations from the great Wenchuan earthquake [J].Earthquake Engineering and Engineering Vibration, 2009, 8(2):179-188.
[4]許 強,黃潤秋.5.12汶川大地震誘發(fā)大型崩滑災害動力特征初探[J].工程地質學報,2008,16(6):721-729.
[5]Han Q,Du X L,Liu J B,et al.Seismic damage of highway bridgesduring the 2008 Wenchuan earthquake[J].Earthquake Engineering and Engineering Vibration,2009,8(2):263-273.
[6]Tanimura S,Mimura K,Nonaka T,et al.Dynamic failure of structures due to the great Hanshin-Awaji earthquake[J].International Journal of Impact Engineering, 2000, 24:583-596.
[7]Wang C J,Shih M H.Performance study of a bridge involving sliding decks and pounded abutmentduring a violent earthquake [J]. Engineering Structures, 2007, 29:802-812.
[8]陳興沖,朱 晞.簡支梁橋支座的空間地震反應分析[J].土木工程學報,1994,27(1):11-18.
[9]Tanimura S,Sato T,Umeda T,et al.A note on dynamic fracture of the bridge bearing due to the great Hanshin-Awaji earthquake[J].International Journal of Impact Engineering,2002,27:153-160.
[10]王軍文,李建中,范立礎.非規(guī)則梁橋橫橋向地震碰撞反應分析[J].振動與沖擊,2010,29(6):25-30.
[11]Chen Y.Modeling and analysis methods of bridges and their effects on seismic responses Theory[J].Computer&Structures,1996,59(1):81 -98.
[12]Kappos A J,Manolis G D,Moschonas I F.Seismic assessmentand design ofR/C bridges with irregular congiguration,including SSIeffects [J]. Engineering Structures,2002,24:1337 -1348.
[13]Lin J H,Zhang Y H,Li Q S,et al.Seismic spatial effects for long-span bridges,using the pseudo excitation method[J].Engineering Structures,2004,26:1207 -1216.
[14]Yin X C,Qin Y,Zou H.Transient responses of repeated impact of a beam against a stop[J].International Journal of Solids and Structures,2007,44:7323 -7339.
[15]Yin X C,Yue Z Q.Transient plane-strain response of multilayered elastic cylinders to axisymmetric impulse[J].ASME Journal of Applied Mechanics,2002,69:825 -835.
[16]Yin X C.Multiple impacts of two concentric hollow cylinders with zero clearance[J].International Journal of Solids and Structures,1997,34:4597 -4616.
[17]徐 然,尹曉春.豎向地震作用下橋面與橋墩的多次重撞擊力的計算[J].工程力學,2010,27(10):124-130.
[18]周 云,宗 蘭,張文芳,等.土木工程抗震設計[M].北京:科學出版社,2005.

