火炮磁流變阻尼器試驗分析與動態模型

李趙春，王 炅

(1.南京理工大學 機械工程學院，南京 210094;2.南京林業大學 機械電子工程學院，南京 210037)

磁流變阻尼器(Magneto-rheological damper，MRD)因為具有阻尼力可調、響應快速，輸出阻力大等優點，目前正廣泛應用于建筑、橋梁、車輛和機械等領域［1－3］。武器系統的反后坐裝置及后坐運動規律影響武器的射擊精度和毀傷率，把磁流變減振技術應用于武器系統的反后坐裝置以減小振動，是具有應用價值的研究方向。目前，國內外已經開始研究將MRD應用武器系統的減振，如Ahmadian等人研究的磁流變阻尼器應用在中到大口徑的槍械系統，研制了用于控制50口徑步槍后坐規律的磁流變阻尼器，研究結果表明，使用磁流變液進行后坐主動控制可減小后坐質量、減小后坐力、提高射擊精度和系統穩定性［4］;南京理工大學設計了用于沖擊試驗臺架的長行程磁流變阻尼器，并通過臺架模擬試驗的方法分析了磁流變阻尼器的動態特性［5－6］。

相對于傳統的反后坐裝置，磁流變反后坐裝置的最大的優點是可以實現半主動控制，而半主動控制的效果很大程度上依賴于MRD動力學模型的優劣。由于MRD的動力學性能受到外加磁場、所受載荷的特點等因素的影響，呈現出強非線性，目前還沒有一致公認的磁流變阻尼器的力學模型。國內外學者研究較多的磁流變阻尼器模型主要有Bingham模型以及考慮剪切稀化的 Herschel-Bulkey模型，Bouc-Wen及其現象模型，修正的Dahl模型以及Sigmoid模型［7－8］等。而這些模型絕大多數都是應用在低速載荷條件下，火炮的后坐過程在高速高沖擊條件下因其載荷與低速條件差別很大，其動力學模型也不同。本文以試驗分析為基礎建立火炮磁流變阻尼器的動力學模型。設計了火炮磁流變阻尼器及其試驗裝置，并進行了性能測試，驗證了該阻尼器在火炮反后坐系統中應用的可行性。提出了火炮磁流變阻尼器的多項式模型，并應用非線性最小二乘法進行了參數識別，在不同控制電流下對比了計算結果和實測結果。結果表明，該模型形式簡潔，精度較高，能較好的反映反后坐過程的阻尼力特性，并且易于求解逆模型，有利于實時控制的實現。

1 磁流變阻尼器反后坐試驗分析

1.1 磁流變阻尼器反后坐試驗裝置

反后坐裝置試驗臺由某型號火炮改造設計而成，如圖1所示，由固定炮架(包含導軌)、炮身、后坐配重、磁流變阻尼器、復進彈簧、軸套、力傳感器和位移/速度傳感器等組成。其中，力傳感器安裝在活塞桿和固定炮架之間，測量由磁流變阻尼器引起的輸出力;阻尼器的外筒與后坐質量固連，形成筒后坐形式;所有后坐部分安裝在固定炮架的導軌上;位移/速度傳感器安裝在固定炮架的底部，可同時測量后坐位移和后坐速度。由八根線性彈簧組成復進機構，主要作用是提供復進力，同時還提供一部分后坐阻力。安裝彈簧時使彈簧有一定的預緊力，其目的是保證后坐部分在復進時能回復到初始位置。

后坐運動由沖擊主動力即炮膛合力Fpt引起，其作用時間短，瞬時能量大，該沖擊主動力在較寬的頻率范圍內存在頻率分量。火炮磁流變反后坐裝置由后坐質量、彈簧、磁流變阻尼器組成，把瞬時的炮膛合力轉化為較為平穩的后坐阻力作用在炮架上，以減小火炮的振動，提高射擊精度。其力學關系如下:

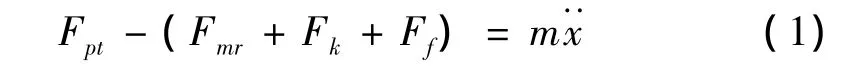
式中，Fmr為由磁流變阻尼器提供的阻尼力，Fk為由復進彈簧提供的彈性力，Ff為導軌對后坐部分的摩擦力，x為后坐位移。m為后坐質量，是火炮身管、后坐配重、軸套等的質量之和。

圖1 火炮磁流變反后坐試驗裝置Fig.1 Firing impulsive facility with recoil MR damper

磁流變反后坐裝置的核心元件是磁流變阻尼器，其結構如圖2所示。考慮加工和安裝方便，采用單筒單出桿形式，無氣囊的結構。由于活塞在不同位置時，腔體內體積不同，因此在灌裝液體時應以內筒和活塞之間的最小體積為準。為提供足夠的阻尼通道長度，阻尼器結構采用三級線圈串聯，同時為滿足后坐行程的長度，設計阻尼器的最大行程為440 mm。表1列出了火炮磁流變阻尼器的主要結構參數的具體數值。

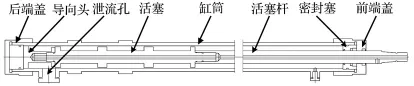
圖2 磁流變阻尼器結構圖Fig.2 Recoil MR damper configuration

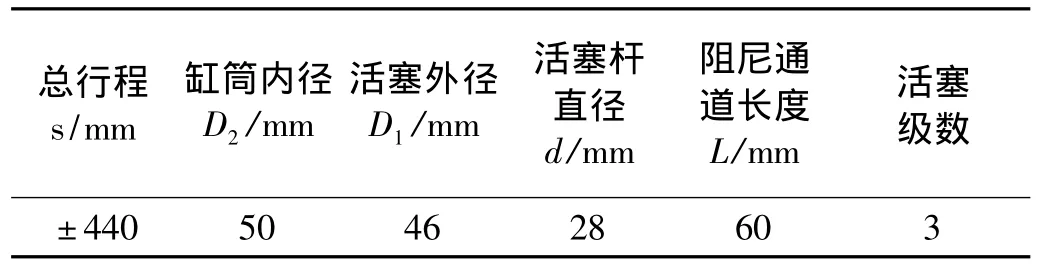
表1 火炮磁流變阻尼器結構參數Tab.1 Structural parameter of the recoil MR damper

1.2 磁流變阻尼器反后坐可行性試驗分析

火炮反后坐裝置的作用是:減小火炮在射擊時的受力;把射擊時全炮的后坐運動限制為炮身沿炮身軸線的后坐運動;把無法控制的全炮后坐變成可以控制的炮身后坐［9］。反后坐裝置的設計目標是在一定的后坐行程條件下，使得后坐阻力FR峰值盡可能小。由式(1)可知，FR=Fmr+Fk+Ff，其中摩擦力 Ff為一固定值;彈簧力Fk=Nkx，與后坐位移成正比，式中k為彈簧的剛度，N為并聯彈簧的根數;Fmr主要由粘性阻尼力Fη和可調庫倫力Fτ組成。磁流變阻尼器在火炮反后坐應用中，可通過調節Fτ來平衡后坐阻力峰值與后坐行程的大小，達到理想的后坐規律，從而減小火炮振動，提高射擊精度。

用圖1所示的試驗裝置，測試磁流變阻尼器在某型號火炮后坐及復進過程中的動態性能。試驗方案為:在相同裝藥、相同射角和相同的環境溫度等試驗條件下，對阻尼器分別施加0 A、0.5 A、1 A、1.5 A 和 2 A的固定電流，按電流值分為五組。為提高測量精度以保證試驗數據的有效性，每組試驗均做三次，試驗數據取算數平均后得測量結果。圖3為施加不同電流時后坐運動諸元圖。

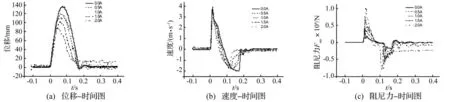
圖3 不同電流下磁流變阻尼器后坐過程諸元圖Fig.3 Recoil dynamics under firing impulsive load

由圖3(a)速度曲線可知，在時間小于0.025 s時，速度變化趨勢不隨施加電流的大小改變，并且速度的峰值相同，說明在這個階段電流大小對后坐速度沒有影響，后坐的運動主要是由炮膛合力Fpt施加給它的動量引起的。分析原因:動量方程(Fpt－FR)t=mv，由該火炮內彈道特性可知Fpt主要作用在0.02 s以內，此時Fpt?FR，則動量方程簡化為:Fptt=mv，因此在該時段內，各電流值對應的速度大致相等。在0.025 s以后，炮膛合力Fpt的影響大大減弱，后坐部分主要受阻尼力和彈簧的彈簧力的作用作減速運動，該階段體現出了因為施加電流的不同，速度減小快慢不同，2 A電流時速度減小最快，1.5 A、1.0 A、0.5 A 其次，0 A 最慢。由圖3(b)、圖3(c)可知，隨著電流的增大，阻尼力峰值依次增大，而后坐位移峰值依次減小，表明了控制電流對磁流變阻尼器的輸出阻尼力和位移具有良好的可調節性。根據不同型號火炮及發射條件的不同，給磁流變阻尼器施加不同控制電流以達到靈活調節后坐阻力與后坐行程的目的。因此，利用本文設計的火炮磁流變阻尼器進行反后坐控制完全具有可行性。并可得出理想的控制規律為:在后坐初始階段，即阻尼力達到峰值之前施加較小的控制電流;峰值之后，隨著速度的減小應逐漸增加控制電流的值，從而保證較小的力峰值和較平穩的過程。

由圖3(a)可知，當電流為2 A時，后坐位移沒有很快回復到初始位置，而是在離初始位置大約10 mm處，以很小的速度復進，而從圖3(c)也能看到這時受到約2 500 N的阻尼力，由于速度很小，其主要為庫倫阻力，與彈簧力保持動態平衡，直至后坐部分回復到初始位置。因此，為保證后坐能快速復進到初始位置應使得庫倫阻力小于彈簧的預緊力，即Fτ＜Fk0。

2 火炮磁流變阻尼器的動態模型

2.1 磁流變阻尼器動態建模分析

本文設計的火炮磁流變阻尼器中使用的磁流變液由LORD公司生產，型號為MRF－132LD。圖4為該液體的剪切稀化特性，由圖可知磁流變液在剪切速率小于150 s－1時表現出明顯的剪切稀化現象。而在高剪切速率時剪切稀化的速率明顯變小，直至液體的粘度趨于某一漸近線。本文設計的火炮磁流變阻尼器工作在高剪切速下，最大速率通常大于105s－1。因此，發生磁流變液剪切稀化的速度范圍遠小于磁流變液在反后坐運動中的速度，對于后坐速度來說，剪切稀化只發生在低速段。

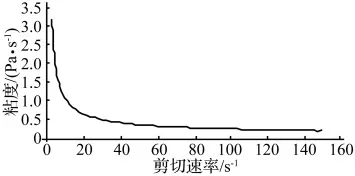
圖4 MRF－132LD磁流變液的剪切稀化特性Fig.4 Shearing thinning behavior of MRF－132LD

火炮磁流變阻尼器中的磁流變液工作在高速高沖擊條件下，目前國內外磁流變阻尼器在沖擊載荷下的動態建模主要有Bingham模型和Herschel-Bulkey模型［10－11］及它們的修正模型。Bingham模型形式簡單、概念清晰，但沒有考慮高速下的非線性因素導致模型偏差較大，雖然通過慣性力修正有所改善，但增加了建模的復雜程度。Herschel-Bulkey模型考慮了剪切稀化現象，但由前文分析可知對于后坐運動來說高速段并不十分適用該模型。同時，由于火炮后坐運動速度很高，磁流變阻尼器動態特性在低速時表現出的滯環特性在高速條件下并不明顯，因此在建模過程中可予以忽略。

2.2 火炮磁流變阻尼器多項式模型

在火炮后坐過程中，阻尼器的輸出力除了粘性阻尼力和庫侖阻尼力以外，實際上還包含了高沖擊條件下慣性力Fi和由于阻尼器空氣腔造成的氣體壓力Fg。它們的大小與后坐過程的動態參數以及阻尼器的結構參數有關。為簡化模型，把慣性力和氣體壓力作為阻尼力的一部分統一建模。

本文在文獻［12］的多項式建模方式的基礎上進行了以下改進:① 忽略滯環特性，統一加速段和減速段多項式;② 增加修正項α(I)，調節曲線縱向的偏移量以達到更好的擬合效果。建立火炮磁流變阻尼器多項式模型，阻尼力可表示為:

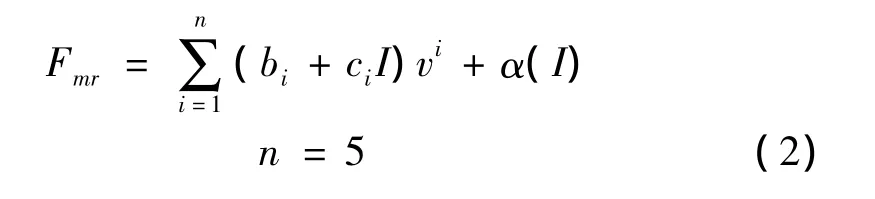
式中bi，ci為多項式系數，α(I)為修正項，作用是調節曲線的縱向位置，與電流大小有關，由式(3)確定。

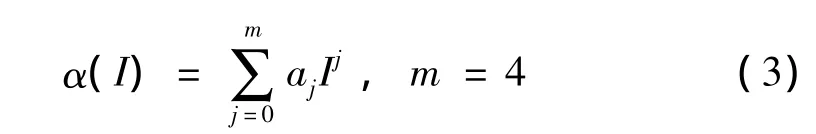
式(2)和式(3)中bi，ci，aj為多項式系數，通過試驗擬合獲得，5階多項式擬合可以同時體現低速時的剪切稀化特性和高速時的慣性力和空氣壓力作用，而且計算量不至于過大，便于實現實時控制。因為該模型中各系數均與電流無關，在控制過程中無需反饋電流信號，使得實時控制容易實現。

由前文分析，火炮磁流變阻尼器可忽略滯環特性，因此加速和減速模型可統一表示。對圖3所示的試驗結果用式(2)進行多項式建模，并用最小二乘法擬合曲線，得到多項式系數aj，bi，ci如表2所示。

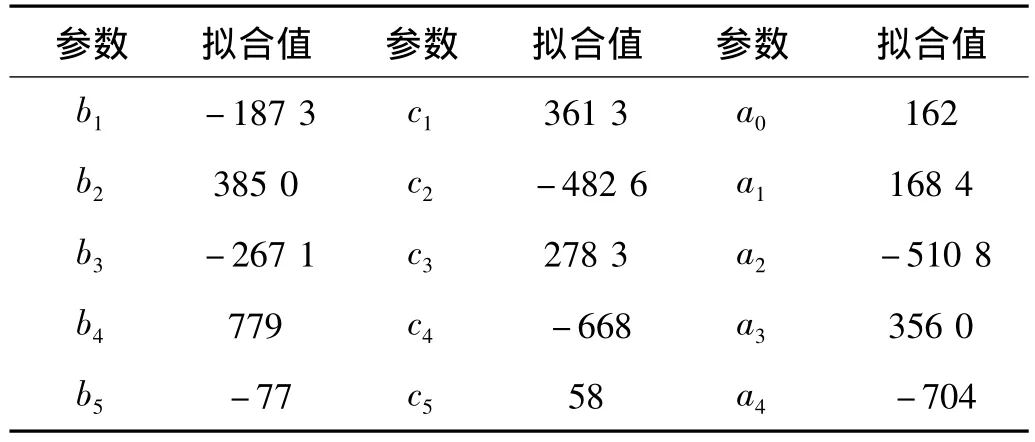
表2 多項式模型各系數Tab.2 Coefficients ai，biand ciof the polynomial model

圖5是在五種不同電流作用下由式(2)擬合的多項式模型結果與文中第1節所得試驗結果的對比，由圖可見模型擬合曲線與試驗值吻合較好。圖5顯示，當速度小于約0.75 ms－1時曲線斜率隨速度的增加逐漸減小，說明該階段剪切稀化效果較明顯，而氣體壓力和慣性力對整個阻尼力的作用很小;當速度大于約1.75 ms－1時曲線斜率隨速度的增加逐漸增大，說明該階段氣體壓力和慣性力對整個阻尼力的影響效果明顯，并且使得本來就較弱的剪切稀化效果完全被抵消。

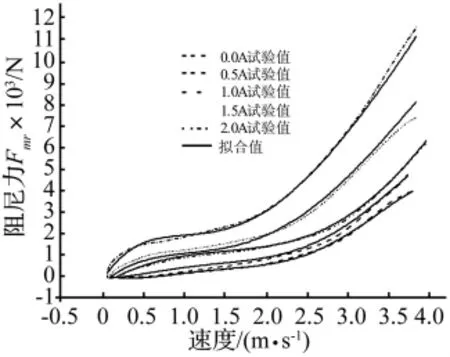
圖5 阻尼力試驗數據與曲線擬合對比圖Fig.5 Co MParison of experimental data and curve fit for the damping force

3 結論

本文以試驗分析為基礎，建立火炮磁流變阻尼器的動力學模型，得到以下結論:

(1)在后坐運動的初始階段，后坐部分主要受炮膛合力影響，而后坐阻力的影響非常小;在初始階段結束之后，炮膛合力極大衰減，后坐運動主要受后坐阻力的影響，此時磁流變阻尼器的對后坐阻力和后坐行程具有良好的調節作用。

(2)火炮磁流變阻尼器的阻尼力不僅依賴于控制電流和后坐速度，還與高沖擊條件下的磁流變效應的復雜性、慣性力、腔體內氣體壓力等因素有關。目前研究較多的磁流變阻尼器的剪切稀化模型和滯回模型均不適合于火炮磁流變阻尼器。

(3)提出用改進的多項式模型描述火炮磁流變阻尼器，該模型的各系數均與電流無關，便于實時控制器的實現。用最小二乘曲線擬合技術進行了參數辨識，擬合了各多項式系數。該多項式模型具有形式簡明，精度高，易于實現半主動控制等優點。為磁流變阻尼器在武器反后坐裝置中的應用提供了理論依據和有效的技術途徑。

［1］Carlson J D.What makes a good MR fluid［J］?Journal of intelligent materialsystem and structure，2003 (13):431－435.

［2］夏永強，余 淼，劉勝龍.磁流變彈性體隔振緩沖器設計及實驗研究［J］.振動與沖擊，2010，29(9):196－200.

［3］王修勇，孫洪鑫，陳政清.旋轉剪切式磁流變液阻尼器設計及力學模型［J］.振動與沖擊，2010，29(10):77－81.

［4］Ahmadian M， Norris J A. Experimentalanalysis of magnetorheological dampers when subjected to impact and shock loading［J］.Communication in Nonlinear Science and Numerical Simulation，2008，13:1978 －1985.

［5］胡紅生，王 炅，蔣學爭，等.火炮磁流變后坐阻尼器的設計與可控性分析［J］.振動與沖擊，2010，29(2):184 －188.

［6］王 炅，胡紅生.一種磁流變減振器沖擊試驗臺架及沖擊試驗裝置［P］.中國專利:200820157119.X，2009－11－04.

［7］Stanway R，Spost on J L，Stevens N G.Non-linear modeling of an electrorheological vibration on damper［J］.J Electr ostatics，1987，20:167 －184.

［8］周 強，瞿偉廉.磁流變阻尼器的兩種力學模型和試驗驗證［J］.地震工程與工程振動，2002，22(4):144－150.

［9］高樹滋，陳運生，張月林.火炮反后坐裝置設計［M］.北京:兵器工業出版社，1995.

［10］李延成.沖擊載荷下磁流變減振器半主動控制研究［D］.南京:南京理工大學，2007.

［11］張莉潔，王 炅，錢林方.沖擊載荷下磁流變阻尼器動態特性分析及模型參數辨識［J］.機械工程學報，2009，45(1)，211 －217.

［12］Choi S B，Lee S K，Park Y P.A hysteresis model for the fielddependent damping force of a magnetorheological damper［J］.Journal of Sound and Vibration，2001:375－383.