長沙市大氣顆粒物PM10質量濃度的統(tǒng)計分布特性

鄧啟紅，黃柏良，唐猛, ，周松梅，劉蔚巍

(1. 中南大學 能源科學與工程學院，湖南 長沙，410083；2. 沈陽鋁鎂設計研究院，遼寧 沈陽，110001)

隨著城市人口的快速增長，能源消耗速度迅速上升，污染物排放大量增加，導致大氣環(huán)境遭遇前所未有的挑戰(zhàn)，居民身體健康受到巨大的威脅。大氣污染物已經成為影響環(huán)境和人類身體健康的主要危害因素之一，特別是其中的懸浮顆粒物由于能對全球氣候和人體健康產生直接的負面影響，近年來引起了各國政府部門和科研機構的高度重視[1?3]。為了控制大氣環(huán)境中顆粒物的質量濃度，降低顆粒物的健康風險，許多國家和地區(qū)制定了日趨嚴格的可吸入顆粒物 PM10和細顆粒物 PM2.5質量濃度排放標準。然而，Saltzman等[4]指出決定顆粒物健康風險因素不僅僅只是顆粒物的質量濃度水平，其質量濃度分布的波動范圍由于增加了風險評估的不確定性也是影響顆粒物健康風險的另一重要因素。不僅如此，流行病學研究表明：顆粒物的健康效應不存在質量濃度閾值[5]，低中度污染事件由于其發(fā)生頻率高也具有較高的健康風險[6]，這表明不同質量濃度所對應的發(fā)生頻率也直接決定其健康風險的高低。因此，評估顆粒物的健康風險必先研究顆粒物的質量濃度水平、波動范圍及其發(fā)生頻率，即顆粒物的質量濃度分布特性[4]。研究顆粒物的質量濃度分布特性也可用于預測顆粒物質量濃度超過國家空氣質量標準的發(fā)生頻率，評估該地區(qū)顆粒物質量濃度達到國家標準所需要的污染源的降低量，從而為政府部門制定顆粒物的控制策略提供有效的參考，促進顆粒物盡快達標，降低其健康風險。大氣顆粒物質量濃度是受污染源散發(fā)強度，氣象條件和地形等諸多因素影響的隨機變量[7]，其質量濃度分布特性可由概率分布函數來描述。在歐美等國家，研究者對大氣污染物的質量濃度分布特性進行了大量的研究工作，多種母體分布函數被用來描述污染物的分布特性，包括對數正態(tài)分布(Lognormal)[8]、韋伯分布(Weibull)[9]、皮爾遜分布(Pearson V)[10]以及伽馬分布(Gamma)[11]等。與此不同，國內在顆粒物質量濃度的統(tǒng)計學分布特性方面的研究卻較少，僅在上海地區(qū)有所開展，發(fā)現大氣環(huán)境中的 PM10質量濃度滿足對數正態(tài)分布[12]。雖然以上母體分布通常均能較好的描述 PM10質量濃度的整體分布特性，但其往往難以準確擬合高質量濃度PM10的尾部分布特性[9]，這直接降低了超標頻率預測的準確度。為了克服母體分布的這一缺陷，準確描述PM10的尾部分布特性，大量研究采用雙參數指數分布來擬合高質量濃度PM10的尾部分布特性。研究結果表明：雙參數指數分布能有效解決母體分布存在的問題，準確描述高質量濃度 PM10的尾部分布特性[13]。為了研究長沙市大氣顆粒物PM10的質量濃度分布特性，本文作者選取4種母體分布函數：對數正態(tài)分布，韋伯分布、皮爾遜分布以及伽馬分布，擬合長沙市大氣顆粒物 PM10質量濃度的整體分布特性，從而確定長沙市PM10的分布類型。采用雙參數指數分布描述高質量濃度PM10的尾部分布特性，進一步預測PM10超過國家空氣質量日平均質量濃度標準的頻率并估計顆粒物質量濃度達標所需要的污染源的降低量，以便為長沙市大氣顆粒物的綜合治理提供科學依據。

1 實驗和方法

1.1 母體分布函數

隨機變量 PM10質量濃度的整體分布特性可以用母體分布的概率密度函數f(x)描述，PM10低于某質量濃度的概率可以用累積分布函數F(x)描述，二者關系如下：則PM10高于某質量濃度xc的高質量濃度發(fā)生頻率為：

例如PM10質量濃度超過國家標準150 μg/m3的概率為 1?F(150)。

本文使用4種理論母體分布函數擬合 PM10的日平均質量濃度整體分布，包括：對數正態(tài)分布，韋伯分布，皮爾遜分布和伽馬分布(表達式見表1)。4種母體分布函數的表達式中均含有2個參數，參數值需根據被擬合的實際樣本估計，估計方程見表2。

表1 4種理論母體分布函數的概率密度函數和累積分布函數Table 1 Probability density function and Commulative distribution function of four theoretical parent distributions

表2 4種理論分布參數的矩估計和極大似然估計方程Table 2 Estimation equations by methods of moments and maximum likelihood for theoretical distributions

1.2 雙參數指數分布

雙參數指數分布FL(x)是Marani等[11]于1982年提出，它是用來描述總體分布F(x)中，高于特定分位數p的樣本點的一種分布函數，二者存在如下關系：

FL(x)的表達式如下：

式中：FL為累積分布函數；y為分布函數的變量；b和φ為分布函數的參數；x為高于分位數p的樣本點組成的新樣本X的樣本值。

雙參數指數分布函數中的參數，可采用經驗分布函數對其進行估計。對應于新樣本X中序號為任意值r(降序排列)的樣本點xr，有：

式中：N為X的容量；)(rx為樣本點xr對應的經驗累積分布函數(r=1，2，…，N)。

將式(6)代入式(4)求得變量ry?，再由式(5)使用最小二乘法對ry?和xr進行線性擬合，即可求出分布函數的參數b和φ。

確定雙參數指數分布的參數之后，可得PM10高于某質量濃度xc發(fā)生的頻率1?F(xc)和回程周期T(xc)[14]：

式中：p為分位數；FL(xc)為雙參數指數分布在xc處的累積分布函數值。

1.3 污染源降低量評估

高質量濃度 PM10回程周期的預測方法也可用于評估達標所需污染源降低量。假設Tm為允許超過標準值150 μg/m3的最小回程周期，ρ為Tm所對應的實際分布中的PM10質量濃度，則達標所需污染源降低量R為：

1.4 實驗數據與處理方法

1.4.1 實驗數據

本文使用的數據由2009年6月至2009年10月間采用大氣顆粒物監(jiān)測儀TEOM(50 ℃)對長沙城市大氣環(huán)境中的顆粒物PM10質量濃度進行的全天24 h實時連續(xù)監(jiān)測得到。TEOM基于微震蕩天平稱質量原理，流量為16.7 L/min，測試單元加熱到50 ℃，每分鐘記錄1次數據。本文中的PM10日平均質量濃度由每分鐘質量濃度平均得到。采樣點位于長沙市西南部某高校校園內，背靠岳麓山，距西二環(huán)約1 km，周邊有輕度工業(yè)污染。采樣期間的平均溫度為28.4 ℃，相對濕度為76.6%，平均風速為1.8 m/s。

1.4.2 數據處理

本文采用矩估計和極大似然估計2種方法對母體分布函數進行參數估計。矩估計是一種最簡單的參數估計方法，利用樣本的各階原點矩來估計理論分布的各階原點矩[15]，極大似然估計是基于極大似然原理的參數估計方法[16]，采用最小二乘法求解參數，4種函數的矩估計方程和極大似然估計方程見表2。

確定各母體分布函數后，還需選取最能代表PM10質量濃度分布特性的分布函數。為此本文采用Chi-squares檢驗和K-S檢驗(Kolmogorov-Smirnov test)評價4種母體分布的擬合優(yōu)度。Chi-squares檢驗值χ2反映了理論頻數和實際頻數的吻合程度，χ2越小，理論分布對實驗值的擬合程度就越好。K-S檢驗值Dmax反映了理論累積分布函數和實際的累積分布函數最大差別，Dmax越小，表明擬合程度越好。

2 結果與討論

2.1 PM10質量濃度水平

圖 1所示為采樣期間 PM10日平均質量濃度變化趨勢圖。在采樣期間的103 d中，長沙市大氣顆粒物的平均質量濃度為93.8 μg/m3，低于國家空氣質量年平均質量濃度二級標準100 μg/m3，但仍有9 d的日平均質量濃度高于國家空氣質量日平均質量濃度二級標準150 μg/m3，對應超標頻率為8.7%。在采樣期間PM10質量濃度呈現出隨月份波動的特征，6～7月污染相對較輕，從9月開始污染逐步加重。長沙市大氣顆粒物PM10的月變化特點主要與該地區(qū)的氣象條件有關，由于6～7月份太陽輻射最強，大氣層對流發(fā)展旺盛，有利于顆粒物的擴散，因此，顆粒物質量濃度較低。

2.2 PM10質量濃度整體分布特性

為了研究長沙市大氣顆粒物 PM10的質量濃度分布特性，首先需確定PM10最符合的理論分布函數。圖2所示為矩估計和極大似然估計得出的理論函數概率密度分布和實際值概率密度分布比較圖，對應的參數的估計值見表3。在確定了分布函數的參數估計值后，可通過Chi-squares檢驗和K-S檢驗比較采用2種參數估計方法所得各分布函數的擬合優(yōu)度，從而選取適當的參數估計方法和最佳母體分布函數來描述 PM10的質量濃度分布特性。

矩估計得到的母體分布函數Chi-squares檢驗值χ2分別為：對數正態(tài)分布10.98、韋伯分布4.82、皮爾遜分布37.06、伽馬分布2.91。極大似然估計得到的母體分布函數Chi-squares檢驗值χ2如下：對數正態(tài)分布為3.45，韋伯分布為 4.81，皮爾遜分布為 6.91，伽馬分布為2.44(如表3所示)。顯然，矩估計的Chi-squares檢驗值χ2均高于極大似然估計的 Chi-squares檢驗值χ2，表明矩估計的誤差較極大似然估計大。尤其對于矩估計得到的皮爾遜分布有p＜0.001，即理論母體分布函數的概率分布與實際質量濃度的概率分布存在顯著性差異，充分說明矩估計的誤差較大。因此，采用極大似然估計能夠更準確的估計 PM10質量濃度分布的參數值。比較K-S檢驗的結果也能得出極大似然估計優(yōu)于矩估計的結論。這一結論與臺灣地區(qū)PM10質量濃度分布的研究結果一致[7]。

在選取了極大似然法作為參數估計方法之后，比較各函數極大似然估計的χ2和Dmax可判斷4種理論母體分布對PM10實際分布的擬合優(yōu)劣。由表3可知：在4種理論分布中，伽馬分布的檢驗值最小，其次為對數正態(tài)分布和韋伯分布，而皮爾遜分布的檢驗值最大。這說明伽馬分布與實際分布的差異最小，擬合程度最高，其次為對數正態(tài)分布和韋伯分布，皮爾遜分布的擬合優(yōu)度較差。根據4種極大似然估計所得母體分布函數，長沙市大氣顆粒物PM10在采樣期間超過國家空氣質量日平均質量濃度二級標準150 μg/m3的頻率和超標天數預測值如下：對數正態(tài)分布為 9.8%，超標10 d；韋伯分布為7.4%，超標8 d；皮爾遜分布為11.7%，超標12 d；伽馬分布為8.3%，超標9 d。由圖1可知：PM10實測數據的超標天數為9 d，超標頻率為8.7%。對比上述結果，同樣可以發(fā)現伽馬分布與PM10的實際分布情況最接近，而對數正態(tài)分布和皮爾遜分布的估計值偏高，韋伯分布的估計值偏低。因此，長沙市大氣顆粒物PM10質量濃度的整體分布特性呈伽馬分布，其形狀參數和尺度參數分別為6.07和15.47。

2.3 高質量濃度PM10尾部分布特性

在使用分布函數預測 PM10質量濃度的超標頻率和回程周期時，分布函數的尾特性決定了預測結果的準確度[17]。雖然母體分布函數能有效的擬合 PM10的整體分布特性，但其往往不能準確描述高質量濃度PM10的尾部分布特性。如圖3所示，在中低質量濃度條件下，4種分布函數對實驗值的擬合效果很好，但在高質量濃度條件下，理論值和實際值逐漸發(fā)生偏離，其中對數正態(tài)分布，皮爾遜分布和伽馬分布高估了高質量濃度的發(fā)生概率。而韋伯分布低估了高質量濃度的發(fā)生概率，說明高質量濃度PM10的尾部分布特性不可用描述 PM10整體分布的母體分布函數進行統(tǒng)一描述。為了有效描述PM10在高質量濃度條件下的分布特征，需采用雙參數指數分布對PM10高質量濃度進行擬合[14]。

圖1 采樣期間PM10日平均質量濃度(2009?06～2009?09)Fig.1 Average diurnal concentrations of PM10 from July 2009 to September 2009

圖2 參數的矩估計和極大似然估計結果Fig.2 Parameters estimated by methods of moments and maximum likelihood

表3 矩估計和極大似然估計的參數值及擬合優(yōu)度檢驗值Table 3 Estimated parameters and goodness of fitting by methods of moments and maximum likelihood

圖3 理論分布與實際分布的高質量濃度PM10發(fā)生頻率Fig.3 Exceeding probability of high PM10 concentration for theoretical distributions and observed data

本文中取分位數p=0.75，即選取 PM10序列中，質量濃度高于0.75分位數的數據組成新樣本X，估計雙參數指數分布的參數。由線性擬合得出：b=0.041，φ=123.688 (如圖4所示)。則雙參數指數分布的表達式為：

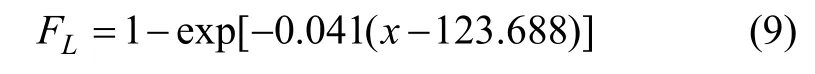
方程的擬合優(yōu)度為0.975，接近1，表明雙參數指數分布能夠很好地描述PM10的極值質量濃度分布。從圖5可以看出：隨著質量濃度的升高，累積分布函數和高污染事件出現的周期呈指數形式增加，這與PM10在高質量濃度處經驗分布函數迅速上升的趨勢保持一致，說明高質量濃度PM10的尾部分布特性符合雙參數指數分布。

圖4 雙參數指數分布的理論擬合曲線、累積分布函數以及回程周期Fig.4 Fitted theoretical line of two-parameter exponential distribution, cumulative distribution function and return period

圖5 母體分布函數和雙參數指數分布函數對PM10極值質量濃度的預測結果比較Fig.5 Comparisons of parent and two-parameter exponential distribution with actual data in high concentration region

圖5所示為母體分布函數和雙參數指數分布函數對高質量濃度樣本的預測值比較結果。從圖5可以看出：雙參數指數分布的預測值與實際值最為接近，擬合情況最好。顯然，采用雙參數指數分布，能夠有效地解決母體分布函數在高質量濃度條件下理論值和實際值存在偏離的問題。

根據雙參數指數的分布(式 9)，PM10質量濃度超過國家空氣質量日平均質量濃度二級標準 150 μg/m3的頻率為0.085，由式(7)有超標回程周期為11.7 d，超標時間約為9 d。顯然，雙參數指數分布的預測值與實際值相符并優(yōu)于母體分布預測結果。這也表明長沙市大氣顆粒物 PM10質量濃度的尾部分布特性屬于雙參數指數分布。

2.4 污染源降低量估計

由于雙參數指數分布對高質量濃度 PM10的分布預測最準確，現采用該分布函數計算PM10質量濃度達標所需的污染源降低量。本文以365 d時間內PM10質量濃度都不超過150 μg/m3為標準，即允許超標的最小回程周期Tm為365 d，此時，PM10超標事件發(fā)生頻率為 0.002 74。在所得雙參數指數分布中，對應該超標頻率的實際質量濃度為233.78 μg/m3，由式(8)得到PM10質量濃度達標所需污染源降低量為35.8%。長沙市對污染源排放的控制還需進一步加強。

3 結論

(1) 在采樣期間，長沙市大氣顆粒物的平均質量濃度為93.8 μg/m3，低于國家空氣質量二級標準，但仍有9 d的天平均質量濃度高于150 μg/m3，實際超標頻率為8.7%。

(2) 長沙市大氣顆粒物PM10質量濃度的整體分布特性呈伽馬分布。理論分布函數中的參數應采用極大似然法進行估計。根據伽馬分布，PM10質量濃度超標的頻率為8.3%。

(3) 雙參數指數分布能有效解決母體分布函數在高質量濃度下與實際值發(fā)生偏離的問題。高質量濃度PM10的尾部分布符合雙參數指數分布，高質量濃度出現的概率隨質量濃度的增長呈指數衰減的趨勢。

(4) 根據雙參數指數分布，PM10超出國家空氣質量日平均質量濃度二級標準的發(fā)生頻率為8.5%。長沙市PM10質量濃度達標所需的污染源降低量為35.8%。

[1] Dockery D W, Pope C A, Xu X, et al. An association between air pollution and mortality in six U.S. cites[J]. New England Journal of Medicine, 1993, 329(24): 1753?1759.

[2] Anderson H R, Atkinson R W, Peacock J L, et al. Meta-analysis of time series studies and panel studies of particulate matter (PM)and ozone (O3)[R]. Copenhagen: WHO Regional Office for Europe, 2004: 186?213.

[3] Pope III C A, Burnett R T, Thun M J, et al. Lung cancer,cardiopulmonary mortality, and long-term exposure to fine particulate air pollution[J]. Journal of the American Medical Association, 2002, 287(9): 1132?1141.

[4] Saltzman B E. Health risk assessment of fluctuating concentrations using lognormal models[J]. Journal of the Air and Waste Management Association, 1997, 47(11): 1152?1160.

[5] Samoli E, Analitis A, Touloumi G, et al. Estimating the exposure-response relationships between particulate matter and mortality within the APHEA multicity project[J]. Environmental Health Perspectives, 2005, 113(1): 88?95.

[6] Abbey D E, Nishino N, Mcnonnell W F, et al. Long-term inhalable particles and other air pollutants related to mortality in nonsmokers[J]. American Journal of Respiratory Critical Care Medicine, 1999, 159: 373?382.

[7] Lu H C. The statistical characters of PM10concentration in Taiwan area[J]. Atmospheric Environment, 2002, 36(3):491?502.

[8] Kao A S, Friedlander SK. Frequency distributions of PM10 chemical components and their sources[J]. Environmental Science and Technology, 1995, 29(1): 19?28.

[9] Georgopoulos P G, Seinfeld J H. Statistical distribution of air pollutant concentration[J]. Environmental Science and Technology A, 1982, 16(7): 401?403.

[10] Morel B, Yen S, Cifuentes L. Statistical distribution for air pollutant applied to the study of the particulate problem in Santiago[J]. Atmospheric Environment, 1999, 33(16):2575?2585.

[11] Marani A, Lavagnini I, Buttazzoni C. Statistical study of air pollutant concentrations via generalized Gamma distribution[J].Journal of Air Pollution, 1986, 36(11): 1250?1254.

[12] Kan H D, Chen B H. Statistical distributions of ambient air pollutants in shanghai, China[J]. Biomedical and Environmental Sciences, 2007, 17(3): 366?372.

[13] Lu H C, Fang G C, Predicting the exceedances of a critical PM10concentration-a case study in Taiwan[J]. Atmospheric Environment, 2003, 37(25): 3491?3499.

[14] Lu H C. Estimating the emission source reduction of PM10in central Taiwan[J]. Chemosphere, 2004, 54(7): 805?814.

[15] Mage D T, Ott W R. An evaluation of the methods of fractiles,moments and maximum likelihood for estimating parameters when sampling air quality data from a stationary lognormal distribution[J]. Atmospheric Environment (1967), 1984, 18(1):163?171.

[16] Wilks D S. Statistical methods in the atmospheric sciences[M].2nd ed. Burlington: Academic Press, 2006: 251?283.

[17] Mijic Z, Tasic M, Rajsic S, et al. The statistical characters of PM10 in Belgrade area[J]. Atmospheric Research, 2009, 92(4):420?426.