基于加速度各向同性的空間光學儀器主動隔振Stewart平臺設計

佟志忠， 段廣仁，何景峰，姜洪洲

(1.哈爾濱工業大學 機電工程學院，哈爾濱 1500010;2哈爾濱工業大學 航天學院，哈爾濱 1500010)

隨著空間光學技術的發展，裝載于航天器上的光學儀器對各種振動源的隔振和減振要求不斷提高，其與航天器剛性直聯的方式已不能滿足高精度、高分辨率的要求。為保證高精度空間光學儀器的儀器精度，必須對其進行多維振動控制。

Stewart平臺具有較高的結構剛度和精度，承載能力大，而且能夠實現多自由度隔振，已被應用于空間光學儀器［1]、整星［2]等主動隔振。但 Stewart平臺自由度之間存在運動耦合、動力學耦合，這種復雜的非線性、強耦合特性使得實現Stewart平臺的高精度控制仍然較為困難。很多學者采用了解耦的立方 Stewart平臺［1，3]，并深入研究了非線性、解耦控制問題［4]，但滿足特定隔振應用的Stewart平臺優化設計的研究較少。

局部各向同性的Stewart平臺，在工作空間的某一點各向同性、局部鄰域內耦合小，更為重要的是易于解耦，便于實現基于解耦控制、集中和分散控制或模態控制的主動隔振。空間光學儀器主動隔振平臺的工作空間很小，因而局部各向同性可作為Stewart平臺設計的一個重要的優化指標［5]。

正交Stewart平臺是解耦的，McInroy等［6]學者對用于主動振動控制的正交Stewart平臺設計及控制進行了深入的研究，基于數值的方法給出了三種具有共同正交幾何特性的機構。Jafari等［7]給出了小范圍工作空間內、滿足正交特性的解析描述。但他們的工作本質上是一種數值方法，研究方法沒有考慮負載的質量幾何特性，所提出的沒有給出柔順中心的解析描述，因而設計滿足給定物理幾何特性的負載以及特定應用的Stewart平臺較為困難。空間光學儀器主動隔振平臺為黑箱振動隔離系統，控制系統一般具有獨立的位置環和加速度環，要求隔振平臺隔離外部擾動(加速度)并保持精密的位置。局部加速度各向同性的Stewart平臺在空間傳遞加速度特性等同，且運動正交，易于實現解耦控制，從而隔離振動、保證位置要求。

為此，本文提出以運動正交、加速度各向同性為指標的主動隔振Stewart平臺設計，考慮負載的質量幾何特性，推導描述加速度各向同性的解析數學表達式，建立描述封閉、完全解析、面向特定應用的設計方法。

1 問題描述

1.1 結構描述

Stewart平臺由上下平臺、六個線性運動的作動器組成，結構滿足鏡像對稱(關于XOY平面的某一軸對稱)和旋轉對稱(沿Z軸旋轉120°對稱)，如圖1所示，其結構由在中位位置的五個參數確定:上鉸圓半徑ra，下鉸圓半徑rb，平臺中位高度H，相鄰上、下鉸點間夾角α與 β。

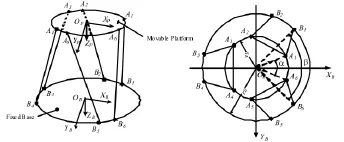
圖1 Stewart平臺坐標定義Fig.1 Definition of the coordinate of Stewart platform

上鉸點在體坐標系{P}的坐標用PA表示，下鉸點在慣性系{B}下的坐標用BB表示。根據對稱性，PA和BB可寫為:

式中:

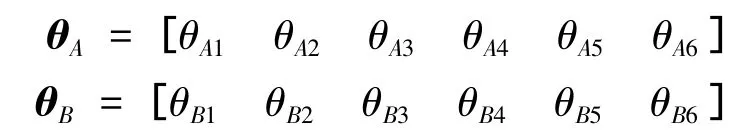
θAi和θBi表示第i號上、下鉸點與 X軸間的夾角，則θA和θB為:

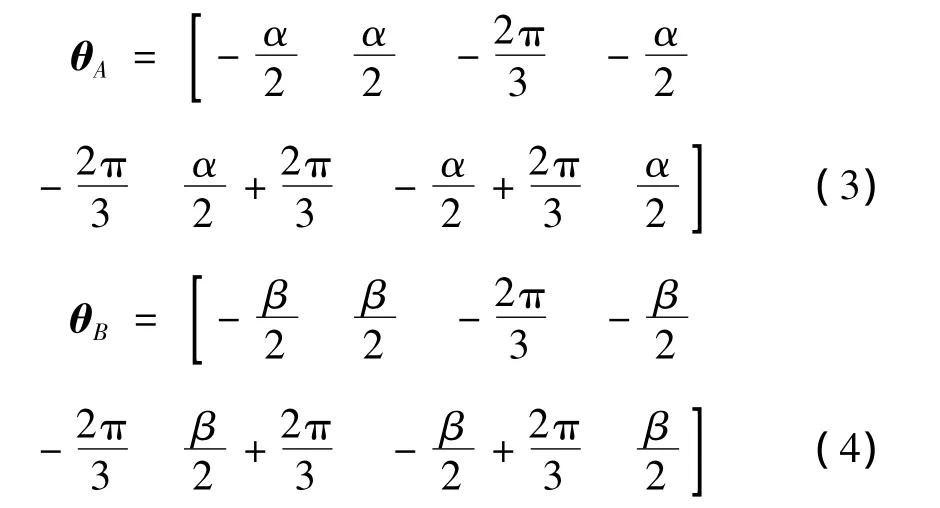
工作空間中Stewart平臺剛體動力學方程的標準形式為［8]:

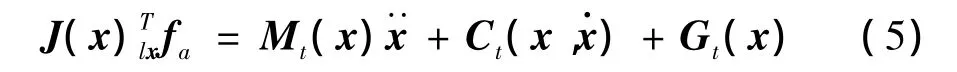
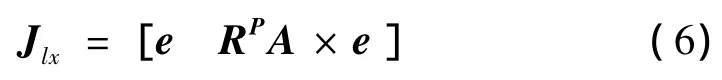
式中:R為方向余弦陣;e為上下鉸點間連線的單位矢量，e=(RPA+，其中Cp為運動參考點，Cp=［0 0 H]T，L為平臺中位時上下鉸點間距離。

如若負載的質心與運動參考點不一致，則負載的慣性矩陣不是對角陣，

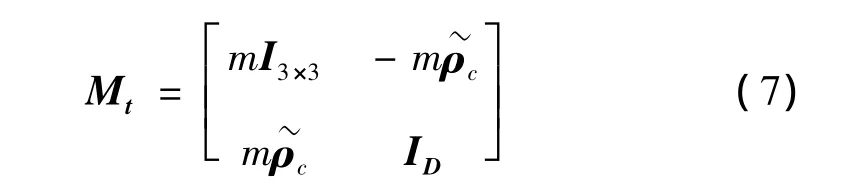
式中:m 為負載質量;ρc為負載質心為負載慣量矩陣，ID=diag(IxxIyyIzz)。

負載慣性矩陣Mt的逆為:

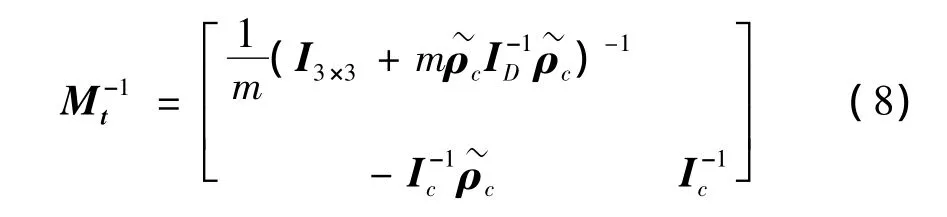
式中:Ic為體坐標系下的負載慣量矩陣。

1.2 加速度各向同性定義及評價指標

一般而言，Coriolis和離心力項可通過逆動力學反饋控制進行補償，而重力項可利用前饋補償或施加重力平衡裝置，這不影響系統的耦合特性，故而式(5)簡化為:

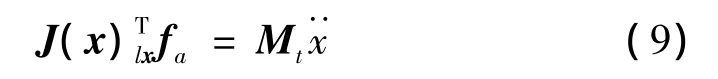
平臺的廣義加速度可描述為:

式(10)描述了關節空間作動器出力與工作空間上平臺廣義加速度間的關系，并且這種傳遞關系不僅與負載的物理特性(慣性)有關，還與負載的幾何特性(質心)有關。為分析和評價這種特性，引入加速度Jacobian陣定義，以G表示:

加速度各向同性以GGT的奇異值評價［9]，即:

加速度各向同性的最優化可用最大奇異值與最小奇異值的比表示，即GGT的條件數:

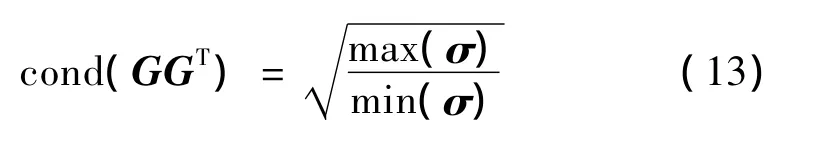
1.3 加速度各向同性與運動各向同性的聯系

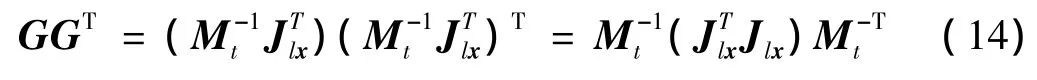
2 加速度各向同性的解析描述

空間光學儀器主動隔振平臺的工作空間很小，且多工作于中位位置，因而本文采用局部各向同性作為隔振Stewart平臺優化設計的一個重要指標。中位時R=I6×6。

2.1 GG T的符號表達形式

對于Stewart平臺而言，通過調整位置或配重在XOY平面使負載質心與運動參考點重合易于實現，即pρc=［0 0 p2]T。將式(11)代入式(14)，有:

式中:

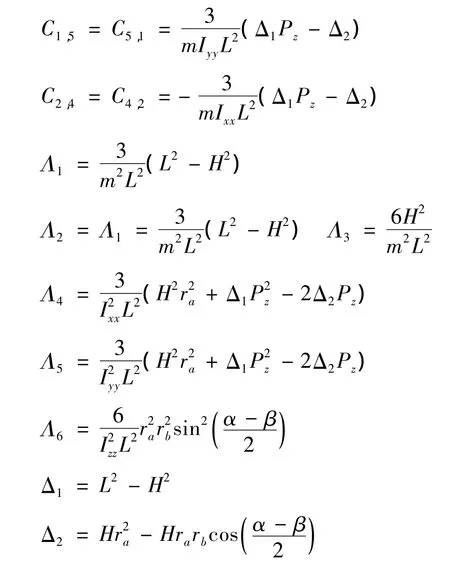
2.3 正交條件

命題1:任一個Stewart平臺必存在柔順中心，且在柔順中心處滿足正交特性。

證明:根據式(15)，GGT是對稱陣。在線性代數中，任一個實對稱陣都有實特征值，存在一個正交陣P，使得P－1(GGT)P。而且，若一個矩陣是實對稱陣，當且僅當其存在唯一的、由規范正交基構成的特征向量陣。故而P為規范正交基構成的特征向量陣時，GGT的特征值為式(15)的主對角線元素，Stewart平臺各自由度正交，稱為正交Stewart平臺。

Stewart平臺滿足正交的條件為:

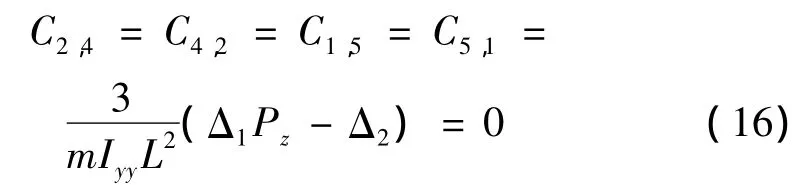
即:

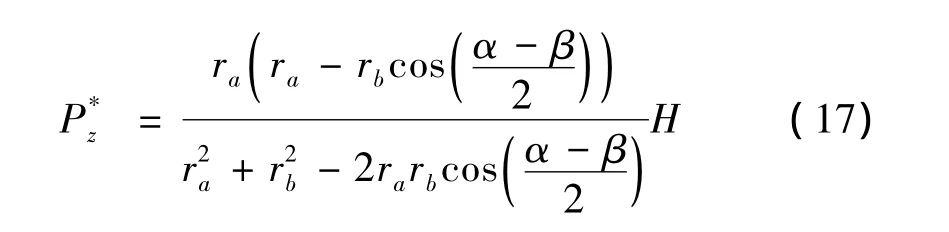
式(17)表明:任一個Stewart平臺必然存在一點，在這點滿足正交特性。若對這一點施加作用力，則只產生平動;若施加力矩，只產生轉動，因此將這一點定義為柔順中心。柔順中心要求負載的質心與平臺中位高度之間必須滿足式(17)，這是Stewart平臺正交的首要條件。

2.4 GG T奇異值的解析形式

Stewart平臺滿足正交特性時，GGT的特征值，即為GGT的主對角線元素，則用于評價加速度各向同性的指標(GGT的奇異值)為:

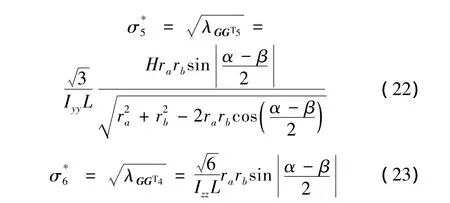
3 基于加速度各向同性的優化設計

基于加速度各向同性的評價指標及其解析的數學描述，本節將推求加速度部分各向同性、完全各向同性的條件，進而實現加速度各向同性的隔振Stewart平臺設計。

3.1 加速度各向同性條件

3.1.1 轉動各向同性

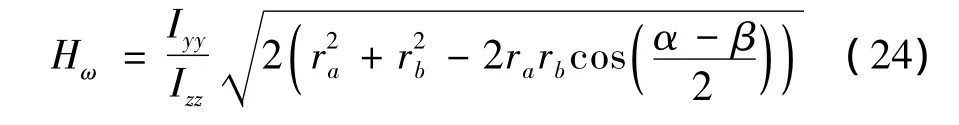
轉動加速度各向同性的性能指標:

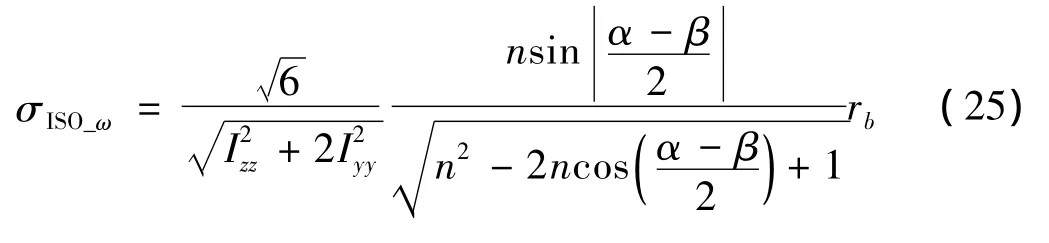
式中n為上下鉸圓半徑之比，n=ra。rb

將式(24)代入式(19)、式(20)，平動加速度各向同性的性能指標為:

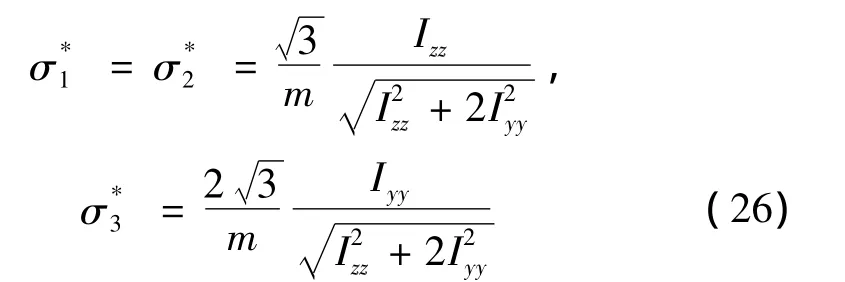
3.1.2 平動各向同性

類似地，平動各向同性的中位高度Hv為:

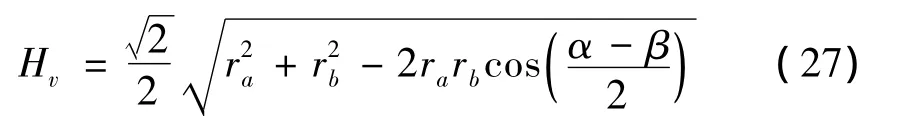
對比式(24)和式(27)可知，相較于轉動各向同性，平動各向同性的條件相對寬松，只與平臺的結構參數有關。將式 (27)代入式(18)～式(23)，得:

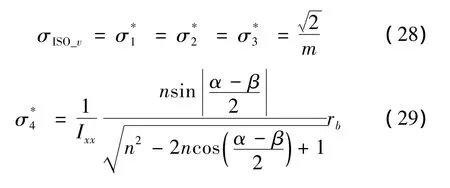
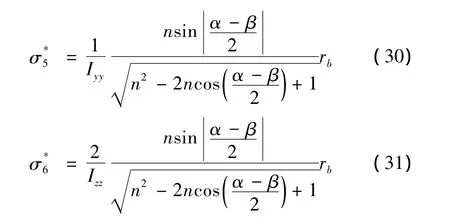
3.1.3 完全各向同性

理論上講，由于平動和轉動量綱的不一致，為分析和達到完全各向同性，必須引入一個特征尺度。然而特征尺度不存在本質的物理描述，Angeles等［10]提出了一種用于工程的特征尺度選取方法。但特征尺度的選取并不唯一，為解決這一問題，本文基于完全各向同性定義特征尺度，以Lscale表示。

根據σISO_v=LscaleσISO_ω，完全各向同性的條件為:

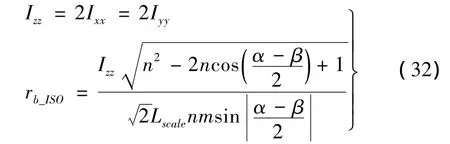
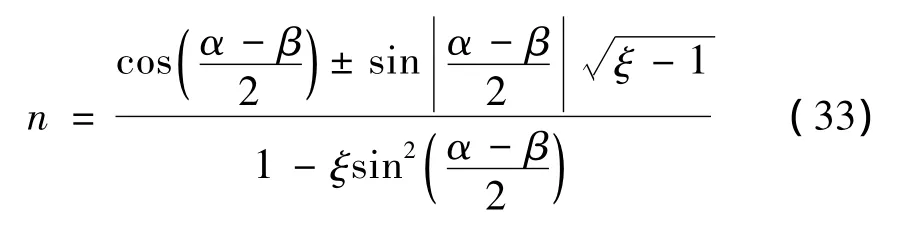
一般而言，n＞2在工程上并不常用且與1/n為對偶機構，故限定0＜n≤2，則下列條件必須滿足:

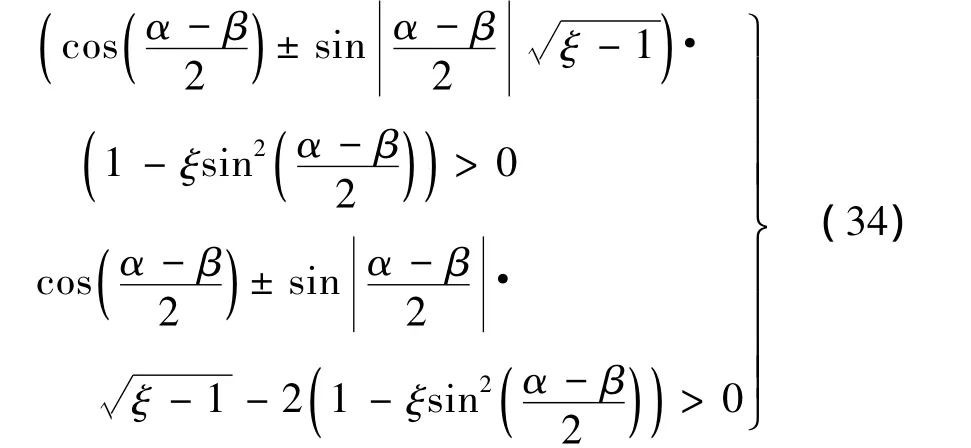
加速度各向同性時，其性能指標為:

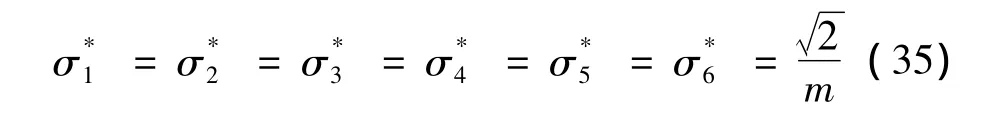
定理1:正交Stewart平臺達到平動或完全各向同性時，必然存在一個特征不變量■2，其只與負載物理屬性有m關。對于具有(k≥6)個支腿、滿足旋轉對稱的廣義Stewart平臺各向同性時，這一特征不變量為

完全各向同性Stewart平臺的中位高度為:

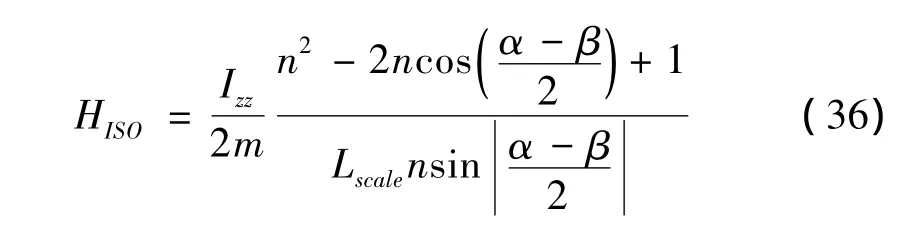
將上式代入式(17)，柔順中心表達式為:

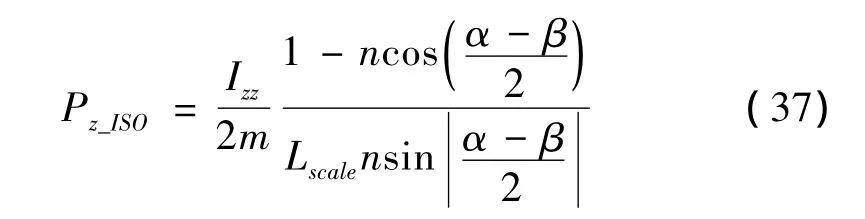
聯立式(32.b)、式(36)和式(37)，得到如下關系:

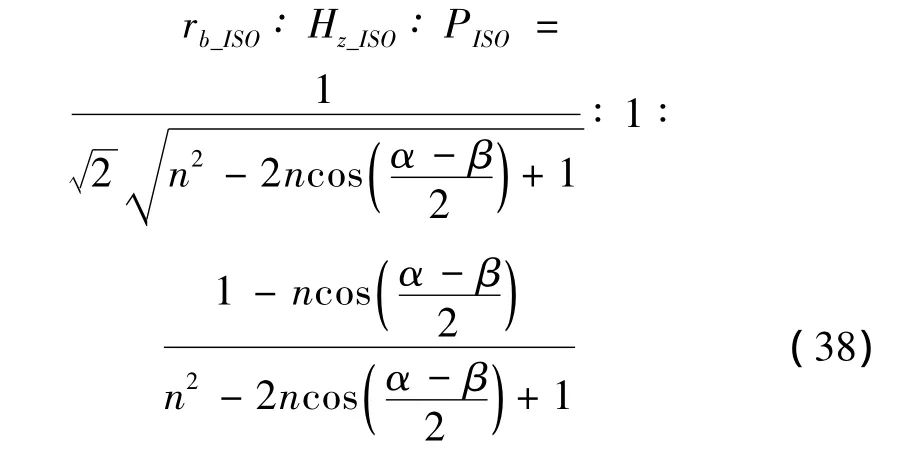
式(32)～式(38)嚴格描述了加速度完全各向同性Stewart平臺的結構參數與負載質量幾何特性之間的關系，但這些工作是基于特征尺度Lscale引入完成的。實際上，這一特征尺度定義是具有廣義性性質的，可視為傳感器的靈敏度，或運動傳動比，抑或是控制系統的反饋比例系數，其是聯結結構設計與控制系統設計的切入點，具有實際意義。盡管這在理論上具有一定局限性，但所推導的數學描述解析、封閉，完全適用于隔振Stewart平臺的設計和工程實際應用。

更為重要的是，加速度完全各向同性要求負載的慣量滿足Izz=2Ixx=2Iyy，而動態各向同性要求Izz=。顯然，后者對負載的物理屬性要求極為苛刻，在工程上幾乎不可能實現，但此時加速度特性是正交的;而加速度各向同性的條件在實際應用中是可以實現的，且能夠保證運動正交。故而，本文選取加速度各向同性作為設計指標之一，既能使隔振平臺對加速度擾動的有效抑制，又能夠保證平臺運動無耦合，從而滿足空間光學儀器的高精度控制要求。

3.2 加速度各向同性的隔振Stewart平臺設計

根據加速度各向同性的解析、封閉的數學描述，設計滿足給定負載特性的、局部加速度各向同性、運動正交的隔振Stewart平臺在理論上是可行的。實際上，3.1節給出了生成一類加速度各向同性隔振Stewart平臺的設計方法，根據上下平臺連接鉸點數的不同，將隔振Stewart平臺分為四種構型:3－3，3－6，6－3和6－6 Stewart平臺。

以3 －3 Stewart平臺為例，此時 α =0°，β=120°，隔振Stewart平臺的結構由以下幾個參數確定:ra，rb、H，以及m、Izz和。表1列舉了不同上下鉸點圓半徑之比的、加速度各向同性的隔振3－3 Stewart平臺構型綜合。

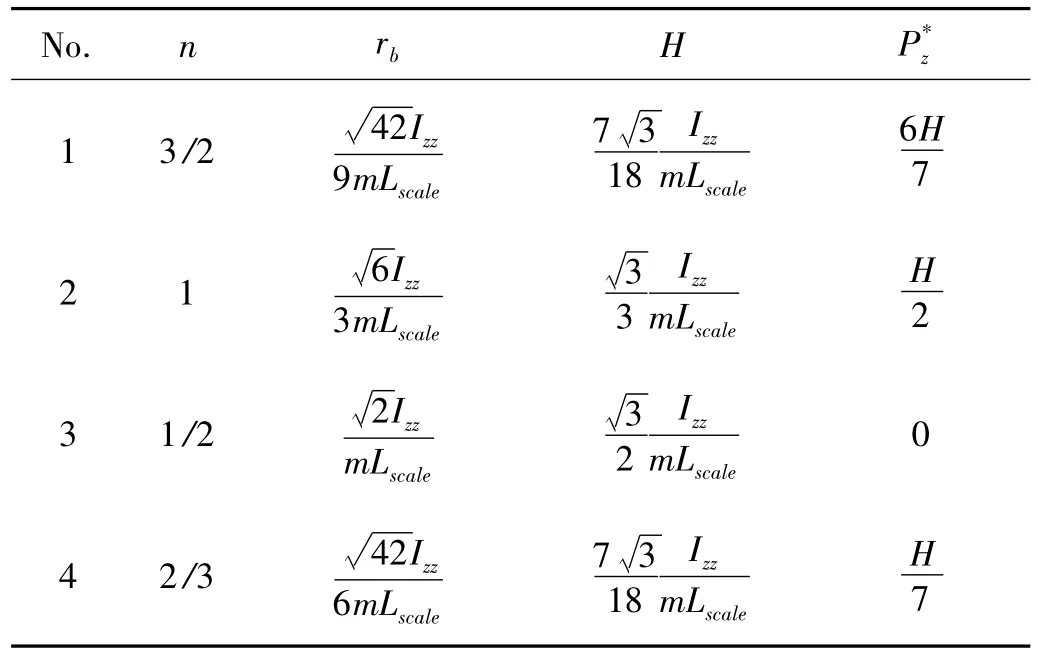
表1 加速度各向同性的隔振3－3 Stewart平臺構型Tab.1 Configurations of vibration isolation 3 －3 Stewart platform with acceleration isotropy

上述設計屬于基于代數法的設計，只能提供一種可行的實現，卻不能保證其是最佳的解決方案。為滿足空間光學儀器隔振平臺的工作空間、無奇異、無構件干涉等要求，必須進行多目標的優化設計和校核。將本文提出的解析設計方法與PSO(Particle swarm optimization)等優化算法相結合，進行優化設計是極容易實現的。以加速度各向同性為指標的隔振Stewart平臺設計，為空間光學儀器的高精度控制系統設計和實現奠定了基礎。

4 結論

本文基于局部加速度各向同性、運動正交特性，給出了用于空間光學儀器主動隔振Stewart平臺的設計方法。與以往工作不同的是考慮了負載質量幾何特性的影響，證明了任一個正交Stewart平臺必然存在柔順中心，并給出了柔順中心的數學表達式。所提出的加速度各向同性數學描述完全解析、封閉，揭示了各向同性、機構結構以及負載特性之間的聯系，建立了生成一類加速度各向同性隔振Stewart平臺的設計方法。

本文下一步工作將研究加速度各向同性、運動正交Stewart平臺的主動振動控制，分析全工作空間的耦合特性及其模態解耦控制技術，為空間光學儀器的隔振提供理論依據。

［1] 劉勺斌，楊洪波，劉 洋，等.基于Stewart平臺的空間光學儀器主動隔振系統研究［J] .噪聲與振動控制，2008，28(2):10－14.

［2] 王曉雷，楊慶俊，鄭鋼鐵.整星主動隔振平臺研究［J] .宇航學報，2007(2):438－441.

［3] Geng Z，Haynes L.Sixa degrees-of-freedom active vibration control using the Stewart platforms［J] .IEEE Transaction on Control System Technology，1994，2(1):45 －53.

［4] 馬 嘉，楊 濤，侯增廣，等.Stewart主動隔振平臺的神經網絡自適應控制［J] .控制與決策，2009，(2):1150－1155.

［5] Merlet JP.Parallel robots，kluwer academic publishers［M] .The Netherlands，2000.

［6] Merlet JE，Hamann J.Design and control of flexure jointed hexapods［J] .IEEE Transaction on Robotics，2000，16(4):372－381.

［7] Jafari F，McInroy JE.Orthogonal Gough-Stewart platforms for micromanipulation［J] . IEEE trans. on Robotics and Automation，2003，19(4):595 －603.

［8] Koekebakker S H.Model based control of a flight simulator motion system ［D] . Delft: Delft University of Technology，2001.

［9] 許益明，趙現朝，高 峰，等.一種新型六維加速度傳感器的結構設計與分析［J] .機械設計與研究，2009(1):48－52.

［10] Angeles J.Is there a characteristic length of a rigid-body displacement［J] .Mechanism and Machine Theory，2006，41:884－896.

［11] Chen Y X，John E M.Decoupled Control of Flexure-Jointed Hexapods Using Estimated Joint-Space Mass-Inertia Matrix［J] .IEEE Transactions On Control Systems Technology，20004，12(3):413－421.