光滑溢流壩過壩水流的二維流場數值模擬及摻氣初生點預測
宋 彧,夏燕芬
(河海大學力學與材料學院,南京 210098)
溢流壩面按其邊界幾何特性可以分為壩頂曲線段、陡坡段、反弧段及反弧后水平段4部分。由于水流情況復雜,至今對溢流壩面的水流流場還沒有一個全面、透徹的認識。而曲線形溢流壩壩面形成摻氣水流,是它具有較高消能率的重要原因之一,所以摻氣初生點位置的確定對壩面階梯設計有著重要影響。近年來,對溢流壩泄流流場以及摻氣初生點的研究逐漸增加。Chanson[1-4]在已有實驗資料的基礎上,分析了壩面流態、摻氣原理以及摻氣濃度的分布規律,總結出壩面阻力系數和摻氣點位置的經驗公式。汝樹勛[5-6]通過模擬實驗,探討了壩面摻氣的形成機理,研究了不同階梯高度下摻氣初生點位置的變化,并給出了確定壩面摻氣初生點位置的計算公式及曲線。
隨著計算機技術的迅速發展、紊流數學模型理論的廣泛應用和計算方法的不斷完善,數值模擬已成為研究溢流壩泄流流場的一條重要途徑。陳群[7]采用非結構化網格,對階梯溢流壩面的紊動流場進行了三維數值模擬,得出了流場速度、壓力、紊動能和紊動耗散率等的分布規律。李靜等[8]用紊流模型模擬了控泄工況下二維和三維數值模擬水面線位置、壩面壓力分布以及流線分布情況,并與物理模型的模擬結果進行了對比。本文利用Fluent軟件,對溢流壩過壩水流二維流場進行數值模擬,給出了不同水頭下自由水面線位置以及壩面沿程流速分布,將紊流邊界層與水流自由表面的交點作為摻氣初生點,并與實驗數據進行比較驗證。
1 外流流場的二維流場數值模擬
1.1 溢流壩過壩水流流場控制方程及邊界條件
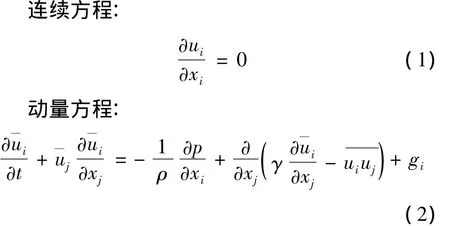
入口邊界采用速度進口邊界,速度值根據設定流量得到,出口邊界采用自由出流邊界,即:取物理量沿水流方向梯度為零,所有氣體邊界都定義為壓力邊界,即壓力為0,固體邊界采用無滑移的固壁邊界。
1.2 計算方法
本文利用非正交網格系統中的SIMPLE[9]算法對溢流壩過壩水流二維黏性流場進行計算,湍流模型采用RNG k-ε模型,自由水面線的形狀及位置采用VOF[10]方法確定,分別對高水頭溢流壩的水面線形狀、壩面壓力及壩面流速分布等進行計算。VOF法可以處理坐標是多值函數的自由表面,具有用一個函數就可描述自由表面各種復雜變化的優勢,是目前計算水力學中處理自由表面水流問題的較理想方法。
1.3 模擬驗證
1.3.1 自由水面線模擬與驗證
圖3給出了Q=2.63 m3/s時不同時刻過壩水流隨時間的流動情況。圖3(a)、(b)、(c)、(d)(e)、(f)分別對應 t=0.5 s、t=1 s、t=1.5 s、t=2 s、t=2.5 s、t=3 s 末時的溢流壩泄流的自由水面線。從圖3中可以看出過壩水流的流動歷時。初始狀態為t=0時;當t=0.5 s時,水舌前鋒已流過壩頂,到達壩面曲線段;t=1 s時,水舌達到斜坡段;t=1.5~2.5 s時,水流向壩面斜坡段下游流動,靠近計算出口區域;t=3 s時,水流已到達出口處。當計算到入口和出口的流量平衡時,就達到穩定狀態。由圖3可知,VOF方法可以很好地跟蹤水流的自由表面。
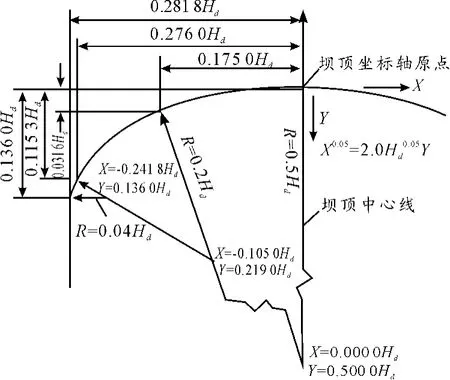
圖1 三圓弧溢流壩上游壩
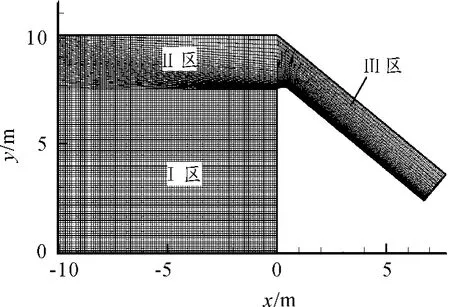
圖2 計算區域與網格劃分
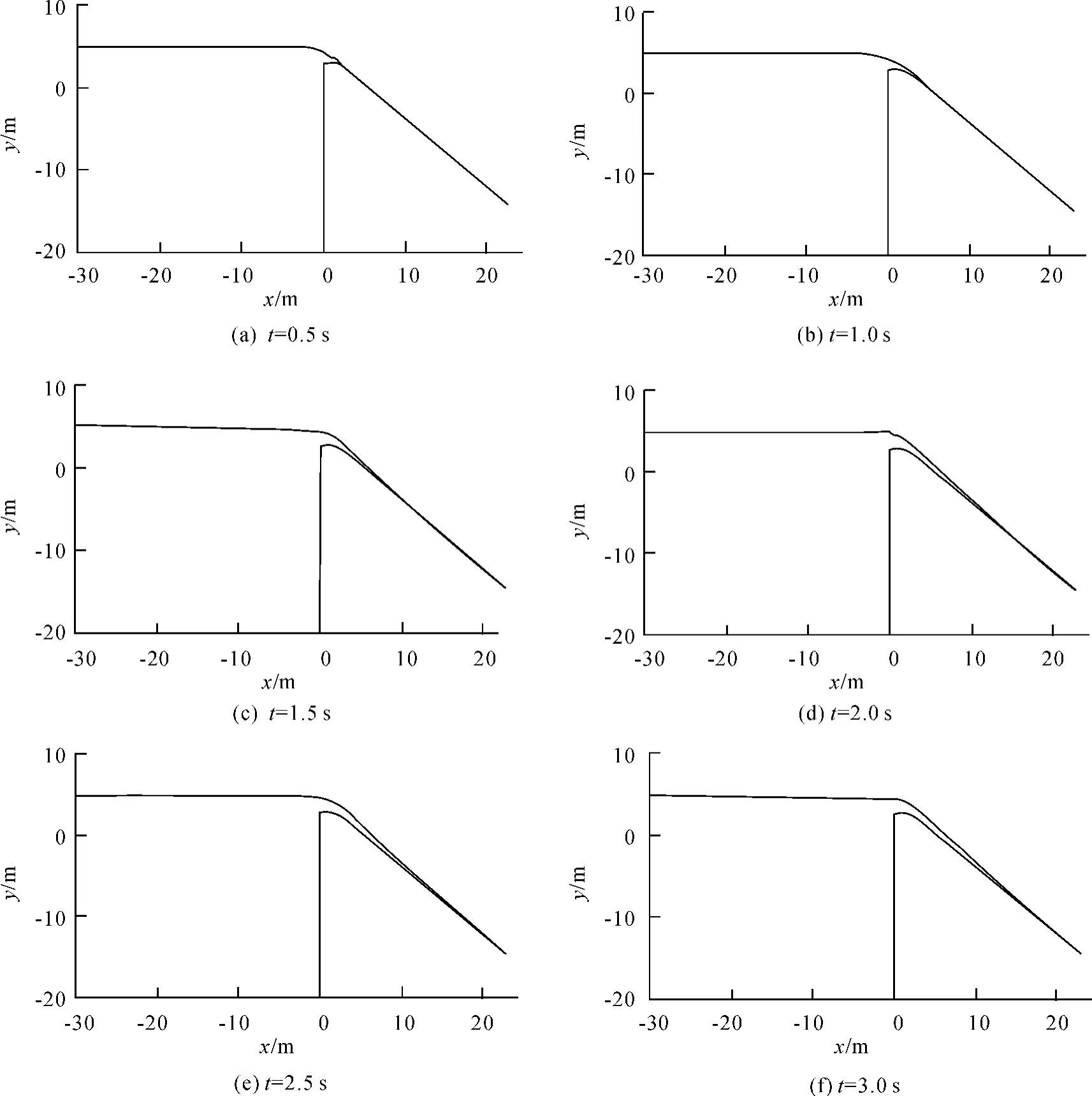
圖3 不同時刻的水流形態(Q=2.63 m3/s)
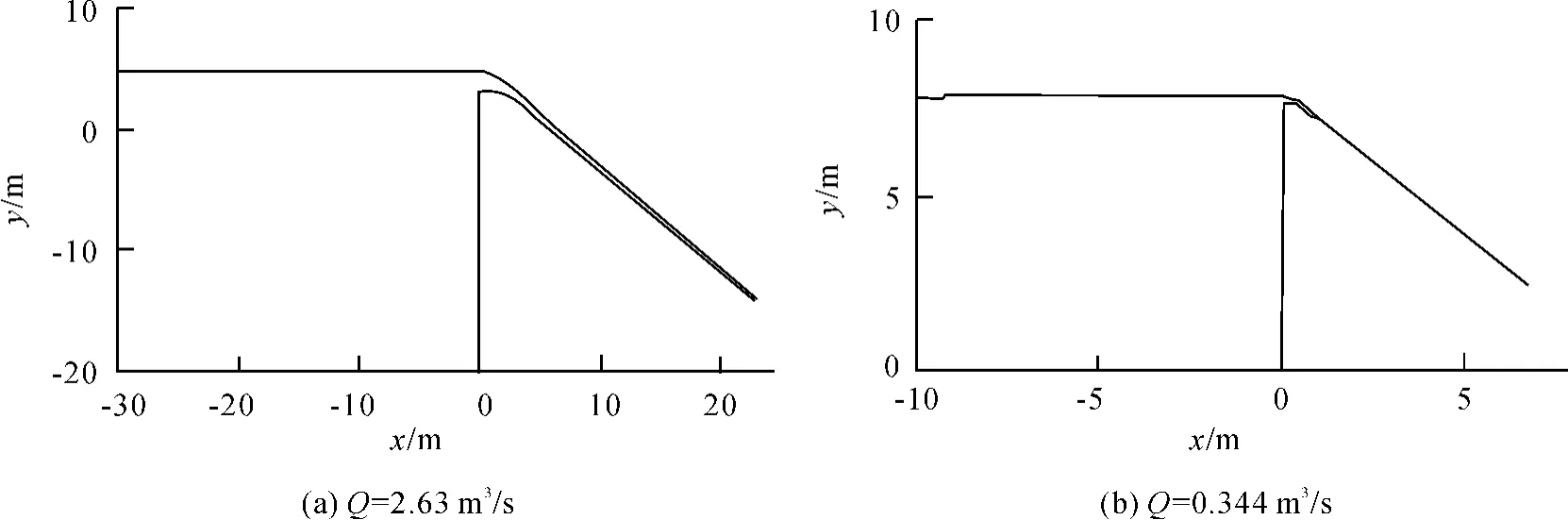
圖4 不同流量下自由水面線
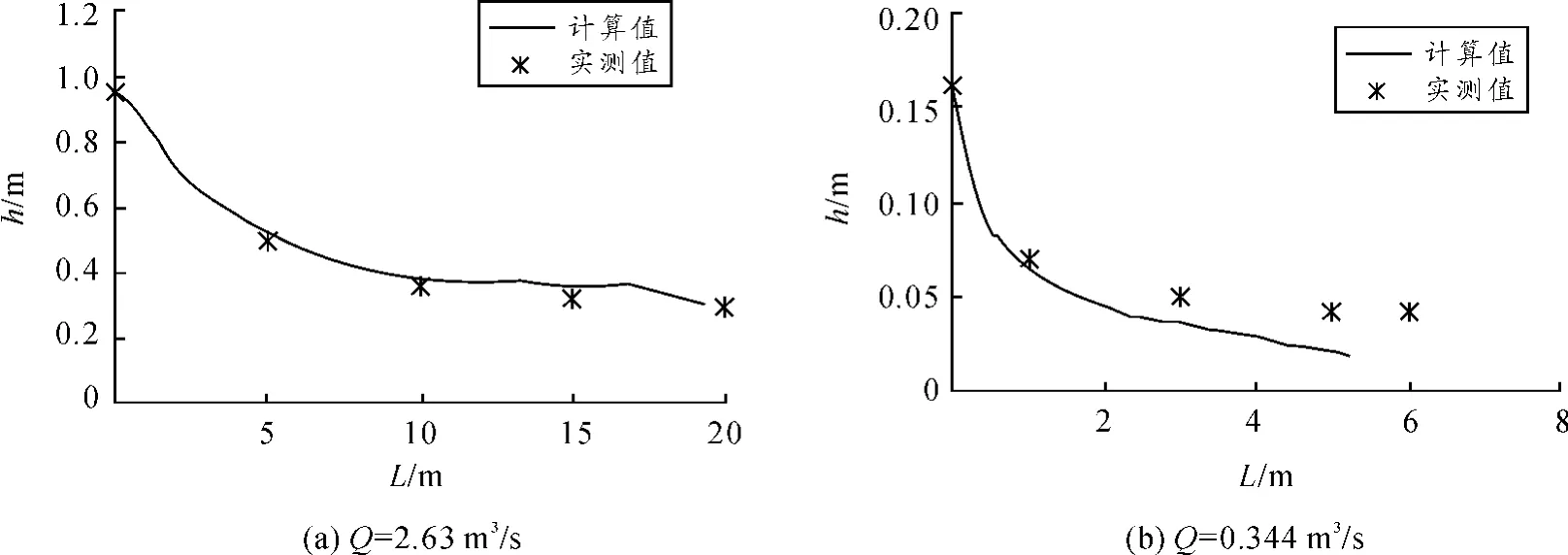
圖5 不同流量下計算與實測的自由水面線
不同流量下計算與實測所得的自由水面線見圖4和圖5。圖4(a)是單寬流量為Q=2.63 m3/s時計算穩定的結果。圖4(b)是單寬流量為Q=0.344 m3/s時的計算結果。由圖4可知,在壩頂處,水深有一個較大的跌落,但是水面線很光滑,說明水流流態很平穩。從壩頂到斜坡,壩面水深沿程逐漸減小。圖5(a)表示單寬流量為Q=2.63 m3/s時的計算值和在格倫馬奇原型溢流壩的實測值[11]比較。圖5(b)表示單寬流量Q=0.344 m3/s時的計算值和鮑爾在試驗槽測得的試驗值[12]比較。圖中L表示與壩頂的水平距離,h表示與河床的垂直距離。由圖可知,在2種流量下,計算值與實測值基本吻合,表明VOF方法與RNG k-ε紊流模型相結合,可以很好地預測溢流壩壩面的水深。
1.3.2 流場和速度場的計算
圖6給出了Q=2.63 m3/s時整個流場內的流線。由圖可知,水流入口處的流線分布很均勻,為均勻速度入口條件。在壩頂以上,流線較密集,說明流速較快。在壩踵處,流線較稀疏,表明這里的流速已很慢。由于壩面的阻擋,流線接近壩面時都向上彎曲,水流沿壩面向上流動。為進一步考察水流沿壩面的速度變化,給出了壩面最大速度沿程變化曲線,見圖7,其中Ue表示最大速度。由圖可以看出,水流速度沿壩面逐漸增加,且不同流量下的最大速度的差值沿程減小。
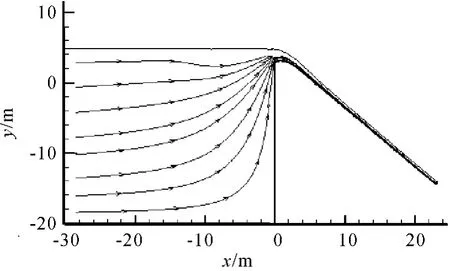
圖6 流量時溢流壩流線
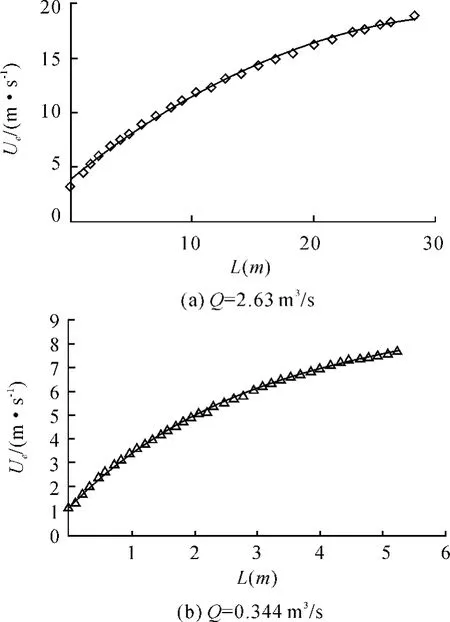
圖7 不同流量壩面最大速度沿程變化曲線
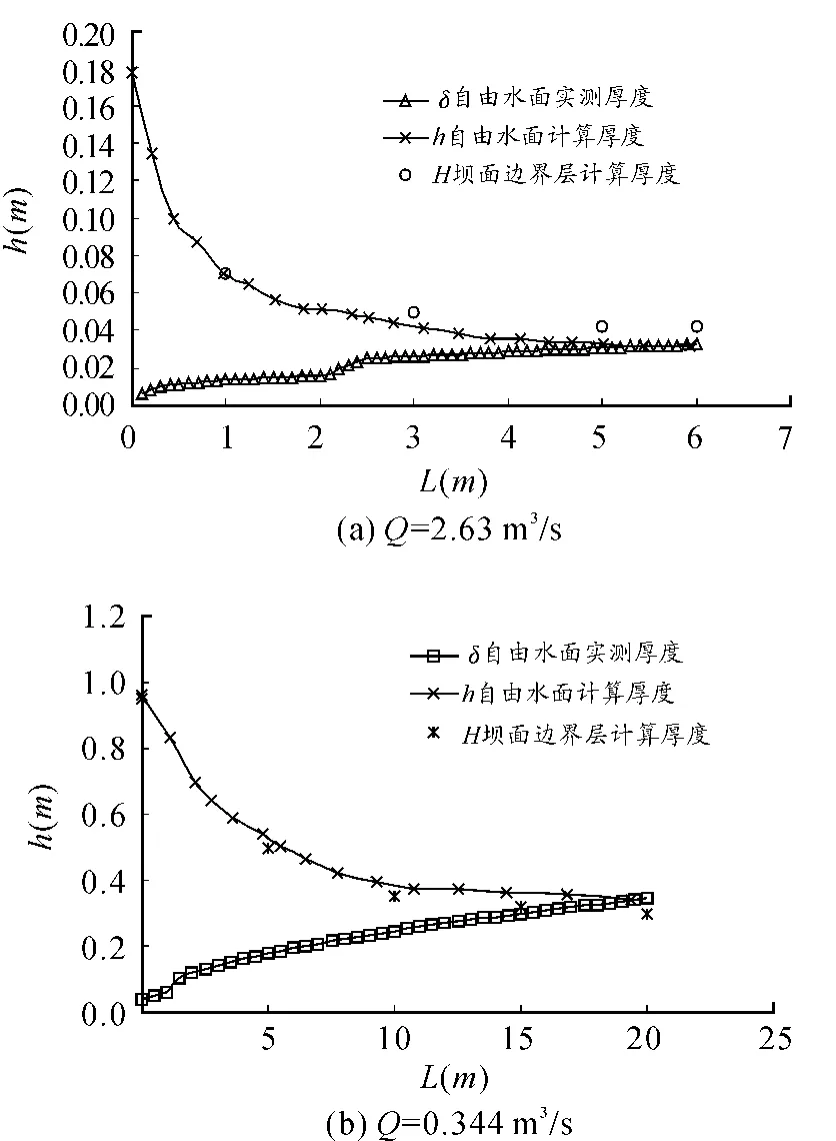
圖8 Q=0.344 m3/s時確定摻氣初始斷面的計算圖
2 溢流壩摻氣初生點的計算與驗證
應用零方程模型[13]對溢流壩上邊界層進行數值求解,模擬得出紊流邊界層厚度沿程發展情況,將它與水流自由表面的交點作為摻氣初生點。
圖8為水流發展后確定摻氣初始斷面的計算圖。由圖8(a)可以看出,在流量等于Q=0.344 m3/s時,離壩頂水平距離6 m時邊界層發展到了水面,實測值在離壩頂水平距離6.5 m左右與實驗值一致,最大偏差7.7%。由圖8(b)知:計算所得的邊界層發展到水面線時離壩頂的水平距離為20 m,與原型溢洪道上觀測的摻氣臨界點很一致,計算值在觀測臨界點上游1~2 m處。這是由于邊界層發展至水面只是摻氣發生的必要條件,只有在表面流體的紊動達到一定強度,克服表面張力,水點越出水面,摻氣才能發生。所以,當邊界層發展到水面時,還應繼續發展一段距離,才能發生水面摻氣。比較圖8中(a)、(b)兩圖可以看出,流量越大,摻氣發生點離壩面的距離越大,使臨界點向下游移動。
3 結束語
1)采用非正交同位網格系統中的有限體積法,通過求解雷諾方程對光滑溢流壩過壩水流二維外流流場進行數值模擬,采用RNG k-ε湍流模型,結合VOF方法確定自由水面位置,計算了2種不同流量下的自由水面線位置、流場以及沿壩面流速分布。通過與實驗資料對比,本文計算的水面線高度與實驗值具有很好的一致性,表明VOF方法可以很好地跟蹤水流運動時的自由表面位置。
2)將邊界層厚度與水面線的交點作為摻氣初生點的位置。將數學模型的計算結果與原型溢流壩得到的實驗值比較,計算值與實驗值很接近,略小于實驗值,證明了自動摻氣水流就是由邊界層發展至水面后開始的。因此,可以用這種數學模型來估算水流的發展和在預定的位置上開始自動摻氣。本文所采用的模型計算方法能很好地預測摻氣初生點的位置,為泄水建筑物的設計提供了可靠的依據。
[1]Chanson H.Stepped spillway flows and air enteainment[J].Canadian Journal of Civil Engineering,1993,20(3):422-435.
[2]Chanson H.Self-aerated flows on chutes and spillways[J].Journal of Hydraulic Engineering,ASCE,1993,119(2):220-243.
[3]Chanson H.Comparison of energy dissipation between nappe and skimming flow regines on stepped chutes[J].Journal of Hydraulic Research,1994,32(2):213 -219.
[4]Chanson H.Hydraulics of skimming flows over stepped channels and spillways[J].Jounal of Hydraulic Research,1994,32(3):445 -460.
[5]Ru Shuxun.Stepped dissipater on spillway face[J].Proceedings of ninth congress of Asian and Pacific Division of the International Association for Hydraulic Research,1994,24 -26(2):193 -200.
[6]汝樹勛.曲線形階梯式溢流壩的消能特性[C]//泄水工程與高速水流論文集.成都:成都科技大學出版社,1994:98-102.
[7]陳群.階梯溢流壩紊流數值模擬及實驗研究[D].成都:四川大學,2001.
[8]李靜,李丹,姜伯樂.帶閘墩溢流壩控泄工況二維與三維數值模擬[J].水利水電科技進展,2011,31(6):10-13.
[9]Patankar S V,Spalding D B.A calcaulation procedure for heat mass and momentum transfer in three-dimensional parabolic flow[J].Int J Heat Mass Transfer,1972(15):1787-1806.
[10]Hirt C W,Nichols B D.Volume of fluid(VOF)method for the dynamics of free boundary[J].Comput Phys,1981,39:201 -225.
[11]Michels V,Lovely M.Some Prototype Observations of Air Entrained Flow[M].[S.l.]:Proceedings of the Minuesota Hydraulies Convention,Part IV,1953:403 -414.
[12]Bauer W J.Turbulent Boundary Layer on Steep Slopes[J].Trans ASCE,1954(119):1212 -1233.
[13]Cebeci T,Smith A M O.Computat ion of Turbul ent Boundary Layer[M].Stanford,California:Stanford Univ Press,1968.

