降雨粒子群散射特性的高效分析

丁大志 沈 鵬 陳如山 尚 社 范曉彥

（1.南京理工大學通信工程系，江蘇 南京 210094；2.空間微波技術國防科技重點實驗室，陜西 西安 710000）

引 言

全球降雨分布及其測量是目前全球環境氣候變化研究中的薄弱環節，當前只有少數國家可以利用熱帶降雨測量（TRMM）衛星獲得可靠的全球降雨分布數據［1-2］。TRMM降雨雷達工作在Ku波段，中心頻率為13.8GHz，可檢測的最小降雨量約為0.6mm／h.為了進一步提高星載降雨雷達對小雨、雪等氣候現象的測量靈敏度，新一代星載降雨雷達將增加K和Ka工作頻段［3］，使得降雨雷達能夠對小雨雪等氣候進行更加精確的測量。因此，對K和Ka波段降雨粒子散射特性及不同頻率對降雨粒子散射特性的影響進行研究對改進天氣和洪水預報、水資源管理以及監測全球變暖與氣候變化具有重要意義。

傳統分析降雨粒子群散射的方法可以概括為兩大類:解析解法和數值近似解法。其中，解析解法主要是分離變量（SVD）法，最早由 Asano等人提出［4］，但是該方法對坐標系的依賴性限制了其對復雜形狀粒子散射特性的研究。隨著計算機硬件環境的發展，數值類方法得到快速發展。用于解決粒子散射問題的計算方法主要包括離散偶極子近似（DDA）法、T矩陣（T-Matrix）法、基于體積分方程（VIE）的矩量法、稀疏矩陣規則網格（SMCG）法等。DDA方法最早由Purcell和Pennypacker在1973年提出，用于分析星際塵埃物質的散射和吸收問題［5］。但是其對存儲量、計算時間的高需求使其發展受到很大限制。T矩陣方法最早由P.C.Waterman［6］于1965年首次引入計算電磁學領域，最顯著的特點是它只與粒子自身的屬性有關，對于某一固定的散射粒子，計算一次它的T矩陣，便可以得到任意方位下該散射體的散射特征，但是在分析非球對稱類模型時，其計算復雜度會大幅度增加。利用體積分方程（VIE）結合矩量法［7］求解宏觀粒子的散射問題，可以精確地分析目標的電磁特性，但是其未知量大、計算時間長等缺點使其只能對較小點尺寸的目標進行分析。SMCG方法［8-9］將傳統矩量法中的阻抗矩陣分為強相互作用矩陣和弱相互作用矩陣，對弱相互作用矩陣進行Taylor級數展開，利用FFT變換計算弱相互作用矩陣與待求向量的乘積，降低了內存需求和計算復雜度。

簡要闡述了電場積分方程和SMCG方法的基本原理。對K和Ka波段下均勻分布的介質降雨粒子的散射特性進行了對比分析，為了更好地模擬實際降雨過程，分析了隨機分布的降雨粒子群的散射特性，研究了一定區域粒徑隨機分布的降雨雨團的散射特性。

1.SMCG方法基本理論

1.1 電場積分方程

對于介質體散射問題，通常可以通過求解表面積分方程和體積分方程來解決。但是，由于降雨粒子為非均勻的介質散射體，一般選擇體積分方程求解散射場。主要針對體積分方程進行介紹。

假設散射體的介電常數和電導率分別為ε（r）、σ（r），r為場點，r′為源點入射平面電磁波在散射體上產生的等效感應電流Jeq可表示為［10］

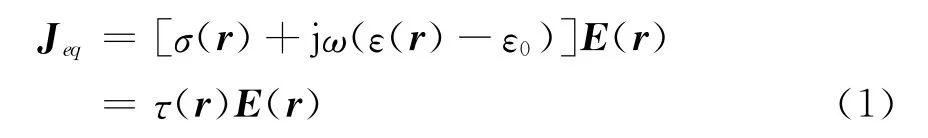
式中:E表示介質散射體上的總電場強度。此等效電流在背景均勻的介質中產生的散射場可以表示為

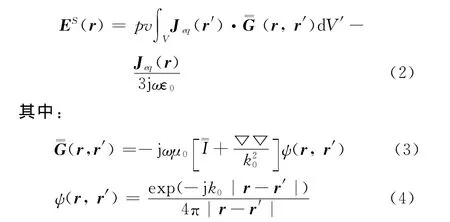
式中:k20=ω2μ0ε0，且μ0為自由空間中的磁導率，pv表示主值積分。

由于介質體的總場強度可以表示為入射場和散射場總和的形式，即

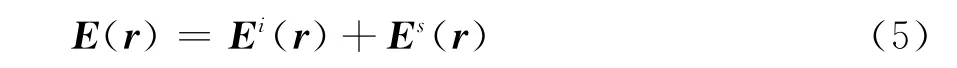
將式（2）代入式（5）可得

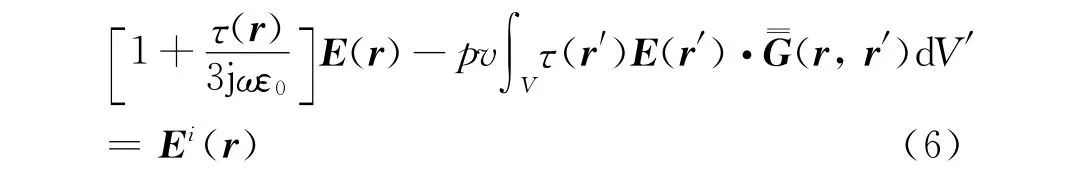
上式便是介質散射體的體積分方程表達式。對于脈沖基點匹配方法，E（r′）·=G（r，r′）可表示為

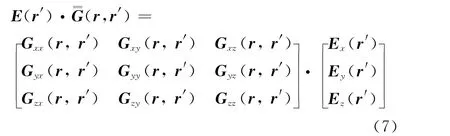
簡化起見，令x1=x x2=y x3=z，則

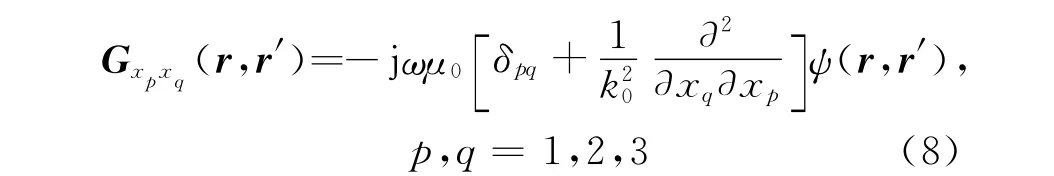
式（7）中的（r，r′）是對稱矩陣，可以將式（6）表示為

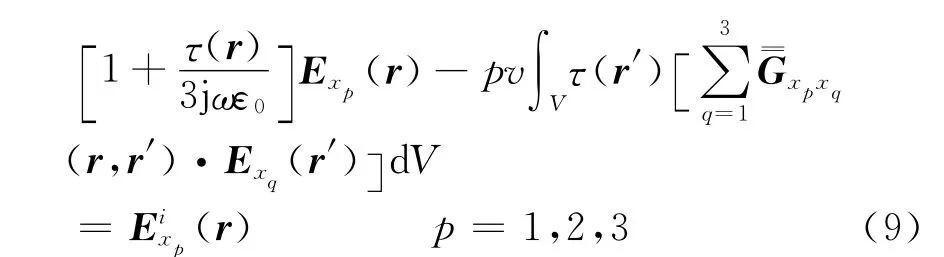
假設介質散射體被剖分為n個小體積單元，每個介質體單元內的E（r）和τ（r）都是常量。第m個體積元的體積表示為Vm，rm表示在Vm內選取的任意點。在每個點rm處，式（6）表示成矩陣方程為

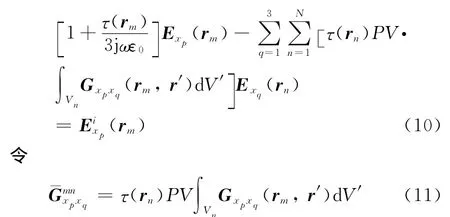
則式（10）可以表示為

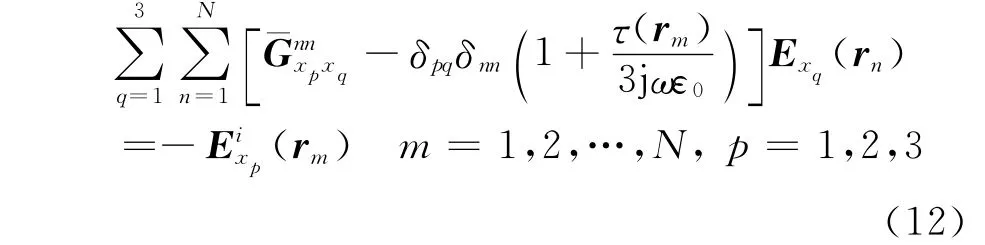
令［Gxpxq］為N×N階的矩陣，其中的元素可以定義為

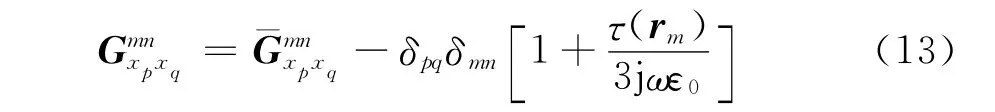
［Exp］和［Eixp］均為N維向量，表示成如下形式

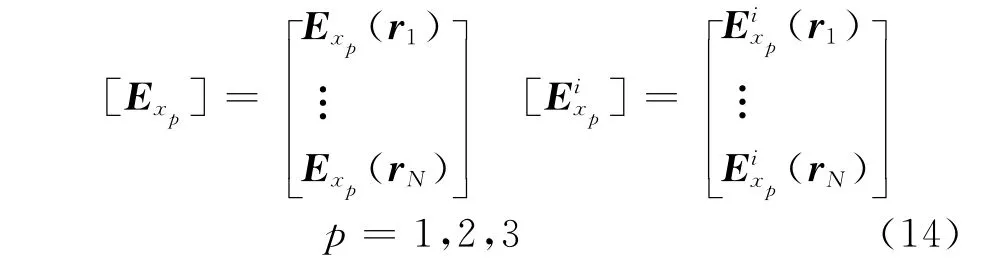
式（6）可以表示成如下矩陣形式

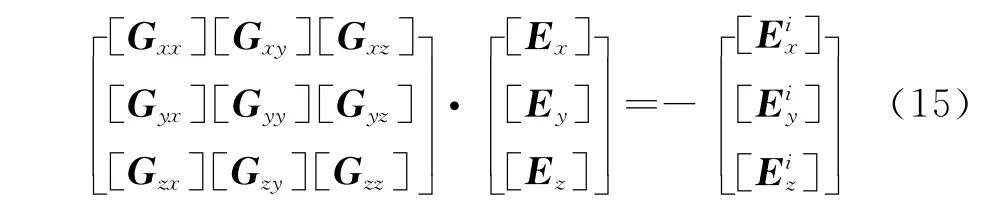
將上式簡化表示為

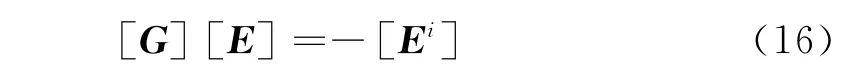
式中:［G］是3 N×3 N 階的矩陣，［E］和［Ei］為3 N維的向量。通過求解上式可以確定N個選定點處的電場。

1.2 SMCG方法

SMCG方法的主要思想是根據剖分單元之間相互作用的強弱將阻抗矩陣劃分成強相互作用矩陣［GS］和弱相互矩陣［GW］

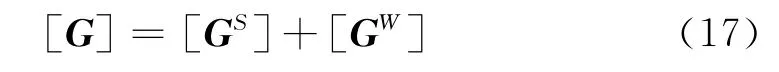
式中:［GS］為稀疏矩陣；［GW］是稠密矩陣。對于［GS］矩陣可以采用壓縮存儲的形式節省內存，而弱相互矩陣矢量乘的計算及存儲耗費了大部分的CPU時間和內存。為加速弱相互矩陣矢量乘的計算，通常采用SMCG快速算法來加速計算。SMCG方法是將Green函數在規則網格點上進行Taylor級數展開，則弱相互矩陣［GW］可以進一步表示為

式中:K為Taylor級數總的展開項數。則式（16）相應的零階和高階解的迭代計算式為

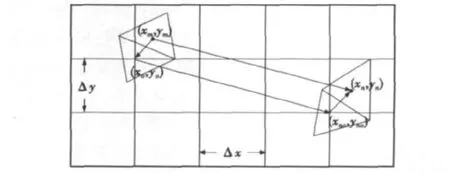
圖1 弱相互作用矩陣元素的直接和間接積分路徑

圖1從二維角度示意了兩種積分路徑，三維情況可以類似推導出。假定介質單元rm=（xm，ym，zm）與rn=（xn，yn，zn）為弱作用的兩個單元，則其阻抗元素G（rm，rn）的積分路徑有兩種選擇:其一是從點rm到點rn的直接路徑；其二是從點rm到其對應規則網格點rmo=（xmo，ymo，zmo），再從點rno到與點rn對應規則網格點rno= （xno，yno，zno），最后，從點rno到點rno.間接計算可以通過格林函數關于規則網格點的Taylor級數展開實現，即

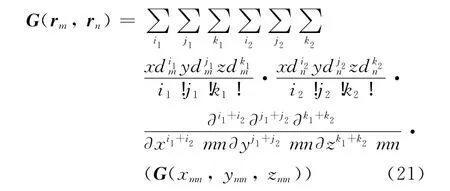
式中:xdm= （xm-xmo）；xdn= （xno-xn）；xmn=（xmo-xno），同理，對應的ydm、ydk、ymn、zdm、zdn、zmn有類似的表示。弱相互作用矩陣與待求向量的乘積可以寫成

式中:［Tsi］相當于將基元素中心點移到與其最近的規則網格點上；［Gi］為Toeplitz矩陣，該矩陣元素反映了規則網格點間的相互作用；矩陣［Tti］相當于將規則網格點移回到檢測中心點。Toeplitz矩陣的行之間滿足循環平移關系，進行矩陣矢量乘時可通過快速傅里葉變換（FFT）實現，SMCG算法能夠將內存需求從O（N2）降至O（N），計算復雜度從O（N2）降至O（NlogN）.

在對弱相互作用矩陣元素進行Taylor級數展開時，需要對近場作用與遠場作用的臨界距離rmax和展開級數所取階數（對應項數）進行折中選取。rmax選取過小、級數展開項過少都會直接造成計算精度的下降；rmax選取過大、級數展開項過多則會占用大量的計算時間和空間。一般選取弱作用距離在Δrg＜rmax＜2Δrg，Δrg表示規則網格間距，Taylor展開階數一般取為2，規則網格點取每波長10～20個點。

對于分析由大量降雨粒子構成的雨團的電磁散射特性，SMCG方法相比于傳統矩量法將有效地降低計算復雜度和內存需求。通過一些典型的算例來分析降雨粒子群的散射情況。由于星載降雨雷達工作在K和Ka頻段，雨滴模型不能直接近似成質點，還需進一步對雨滴模型進行細分成更小的單元，利用正六面體單元對雨滴模型進行了剖分細化。

2.實驗結果分析

Pruppacher等人［11］通過對大量實驗數據分析指出，降雨粒子半徑在小于140μm時可以等效為球形，當半徑大于140μm雨滴的形狀通常呈橢球形。

降雨粒子的數學模型通常等效為橢球，因此，在研究降雨粒子散射特性時，主要針對橢球形粒子模型的電磁特性進行分析。假設等效后橢球的旋轉軸為z軸，對應軸長為b，在x，y方向上的橢球軸長為a，則直角坐標系下的橢球方程可寫為

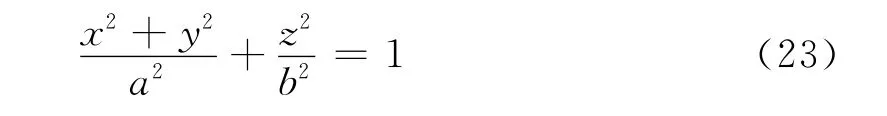
當a＞b時，稱之為扁橢球；a＜b時，稱之為長橢球；特殊情況下，a=b時為球模型。

在實際降雨過程中，降雨雷達觀測到的都是大量降雨粒子構成的雨團信息。大量的實際觀測數據表明，構成雨團的降雨粒子大都滿足某種粒徑分布（如:L-P，M-P，Gamma分布）的形式。粒徑分布是指在一定觀測空間中的大量粒子，其粒子半徑的數學統計分布形式。針對粒徑分布呈隨機分布的模型進行了散射特性的分析，隨機是指粒子半徑大小在一定范圍內是隨機的。

針對仿真分析，入射電磁波的工作頻率是基本參數。例如:現有的TRMM型降雨雷達入射電磁波的工作頻率選取在Ku波段，這主要是考慮到Ku波段波長較長，具有很好的探測能力。而K和Ka波段的入射波波長較短，與降雨粒子的等效半徑基本保持在一個數量級。粒子尺寸、相態等參數的變化對其散射特性的影響很明顯。新一代的降雨雷達（PR2，Precipitation Radar 2）就將 K和Ka工作頻段下降雨粒子的電磁特性作為重要的觀測對象。因此，從接近實際情況的角度考慮，本文選取K和Ka波段作為工作頻率。

降雨粒子模型對電磁波的折射參數選取可以參考水和冰的復折射指數數據［12］。Ka波段下水的復折射參數在1.784+0.0013i到4.954+2.79i的范圍內。

2.1 固定方位下球形降雨模型的散射特性

圖2所示為直徑1mm的27個球形降雨粒子，均勻分布在空間中，球心距為1.6mm，復折射參數選取為（2.0，0.01），入射波工作頻率為37.5GHz，波長λ=8mm，沿z方向入射，且只有x方向的電場。SMCG方法將粒子剖分后未知量為5859，強弱相互作用的臨界距離取為rmax=1.4Δrg；泰勒級數展開的階數為γ=2.

從圖2可以看出:SMCG方法所得計算結果與VIE結合矩量法計算所得角分布曲線吻合，從而可以驗證本文所采用SMCG方法的正確性。表1給出了SMCG方法和VIE方法在內存消耗和計算時間上的比較。從表中可以看出:在保證計算精度的前提下，SMCG方法大大節省了計算時間和內存消耗。

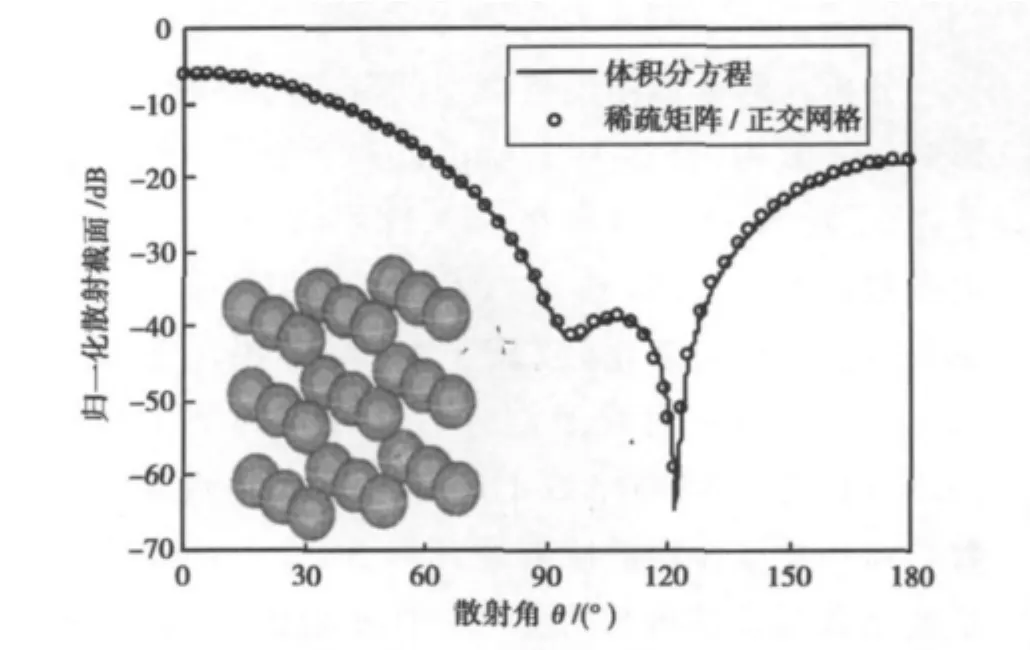
圖2 降雨粒子群在固定方位下SMCG法和VIE結合矩量法計算所得水平極化散射特性

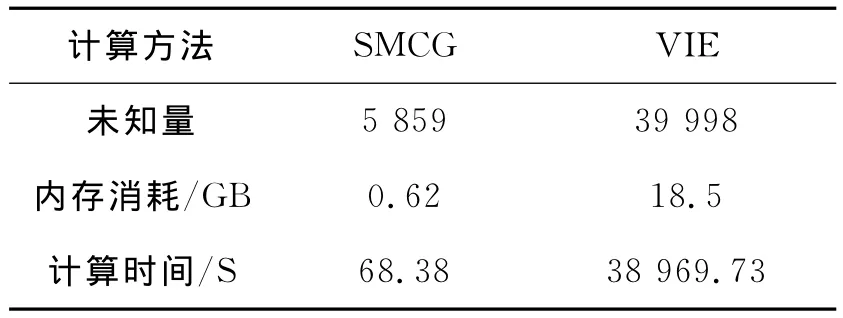
表1 SMCG和VIE方法耗時和內存消耗對比

2.2 降雨粒子群在均勻／隨機分布下的散射特性

對于微波遙感而言，降雨粒子在空間的分布通常是隨機的，僅僅研究均勻分布下粒子的散射特性便不足以滿足實際情況的需求。我們對比分析了球形降雨粒子在均勻／隨機分布下的散射特性和不同軸比的橢球近似雨團模型均勻分布對散射特性的影響。降雨粒子團在空間的隨機分布采用蒙特卡羅法來模擬，且粒子間相互分開不接觸。以125個球形降雨粒子模型隨機分布在1λ×1λ×1λ空間中為例，圖3描述了該模型的空間分布情況。對比分析了均勻／隨機分布和不同軸比的降雨粒子對散射特性的影響。

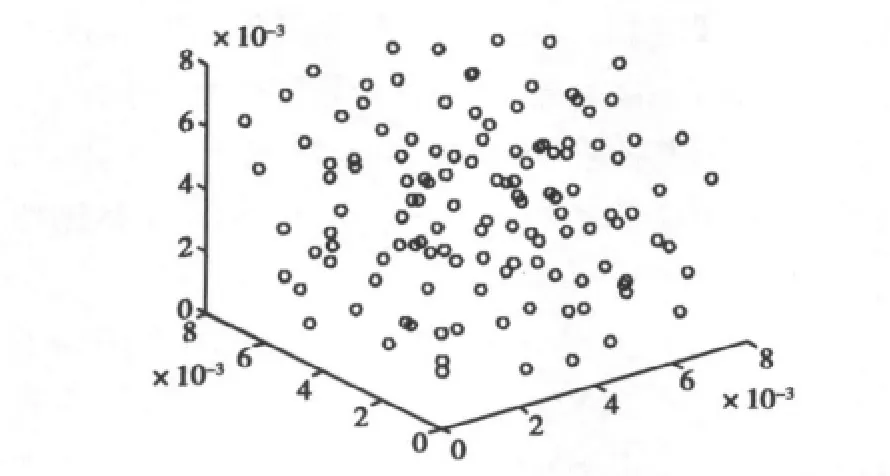
圖3 降雨粒子團在1λ×1λ×1λ空間中隨機分布模型

分析球形近似雨團模型空間分布對散射特性的影響。參數為:直徑為1mm的125個球形降雨粒子，粒子均勻／隨機分布在1λ×1λ×1λ空間中，復折射參數選取為（2.0，0.01），入射波工作頻率為37.5 GHz，沿x方向極化，波長λ=8mm，沿z方向入射。SMCG方法將粒子剖分后未知量為27125，每一維方向上規則網格數Ng=16（Ng為規則網格數），強弱相互作用的臨界距離取為rmax=1.4Δrg；泰勒級數展開的階數為γ=2.圖4描述了125個同樣尺寸的球形近似降雨粒子模型在空間中均勻分布和隨機分布兩種情況下的電磁特性。從圖中可以看出:當散射角較小（接近前向散射）時，兩種分布對散射結果的影響并不明顯；隨著散射角的增大，兩種分布下的散射強度存在著明顯的差異。換言之，入射波入射方向的不同對散射體的前向散射影響不大。

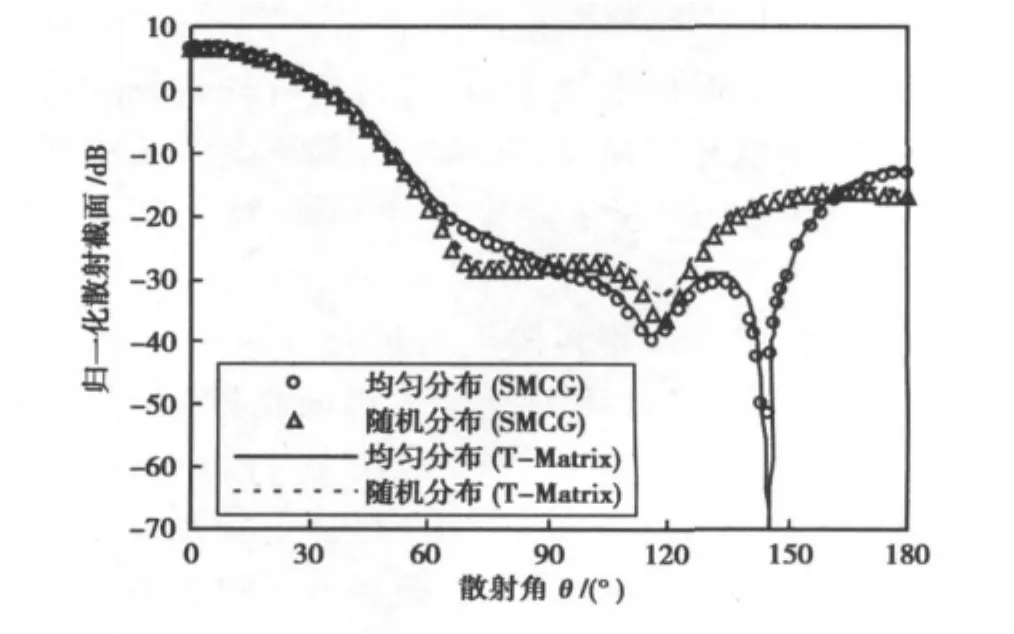
圖4 直徑為1mm的125個球形降雨粒子均勻／隨機分布于1λ×1λ×1λ空間中的粒子團模型在Ka波段下的散射強度

分析不同軸比的橢球形近似雨團模型均勻分布對散射特性的影響。參數為:等效球直徑r≈1mm，軸比分別為1.0、1.5和2.0，z軸為旋轉軸的125個扁橢球形降雨粒子，粒子均勻分布在1λ×1λ×1λ空間中，復折射參數選取為（2.0，0.01），沿x方向極化的入射波波長λ=8mm，沿z方向入射。粒子剖分密度不變，以上不同軸比粒子剖分后對應的未知量分別為27125，27375，27875，Ng=16，rmax=1.4Δrg和γ=2.

圖5描述了不同軸比的橢球降雨粒子模型的散射特性，模型具有相同的等效球半徑。從圖中可以看出，軸比的不同對模型的前向散射和后向散射影響均不是很大，散射強度的第一個谷點隨著降雨粒子軸比的增大而逐漸減小，且谷點的位置也向左偏移，這是由于軸比越大，模型的非球形效應越明顯。

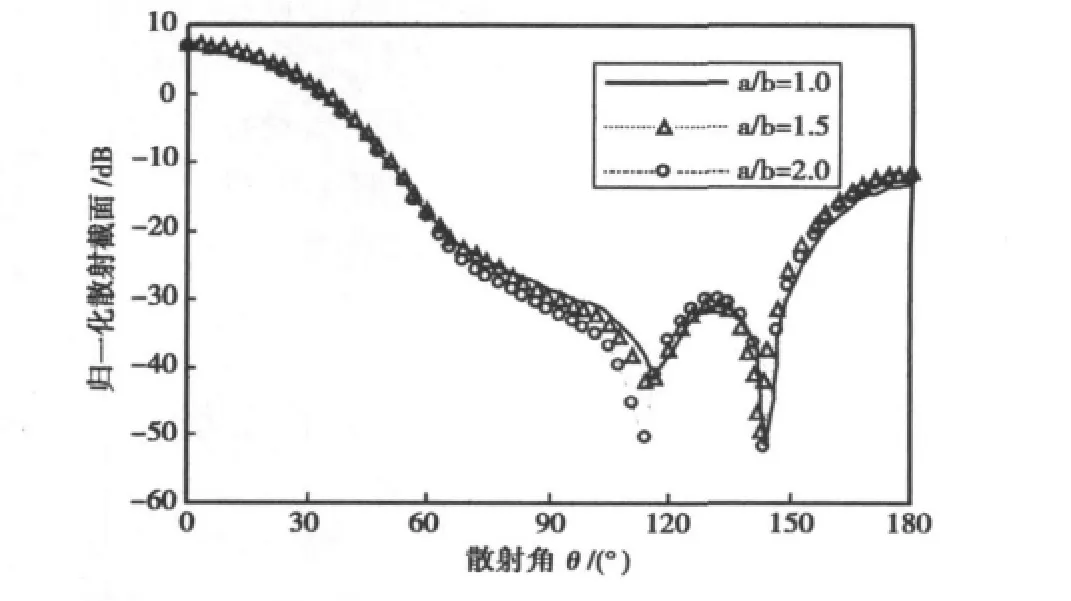
圖5 等效球直徑為1mm的125個軸比分別為1.0、1.5和2.0的橢球形降雨粒子均勻分布于1λ×1λ×1λ空間中的粒子團模型在Ka波段下的散射強度

2.3 降雨粒子群在不同頻段下的散射特性

實際現象表明，降雨粒子在不同頻段下的散射特性存在著明顯的不同。這是因為當電磁波投射到氣體分子或液態、固態的云和降雨粒子上時，一部分能量被散射，另一部分能量被吸收而轉變為熱能或其它形式的能量。對隨機分布在一定空間中的大量降雨粒子在不同頻率點處的散射特性進行了研究。為了建立盡可能逼近現實的降雨模型，獲得所選雨滴模型的理想極化參數，雨滴的軸比選擇特別重要。Pruppacher等人［11］提出的雨滴軸比與等效直徑的關系為

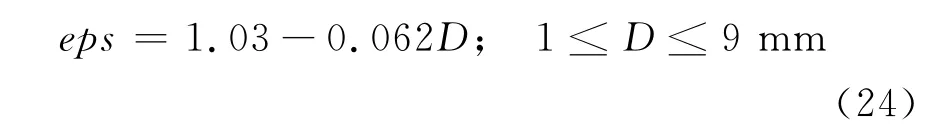
Beard等人［13］通過對試驗數據的擬合得到的多項式關系為

Andsager等人［14］對諧振雨滴群的形狀進行平均，得到的軸比公式為

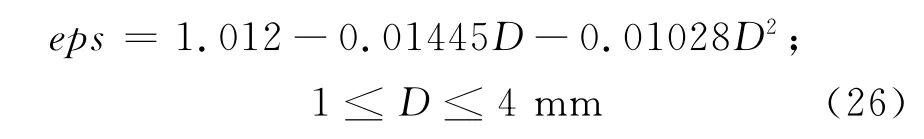
Keenan等人［15］對文獻中一些雨滴模型的參數擬合結果為

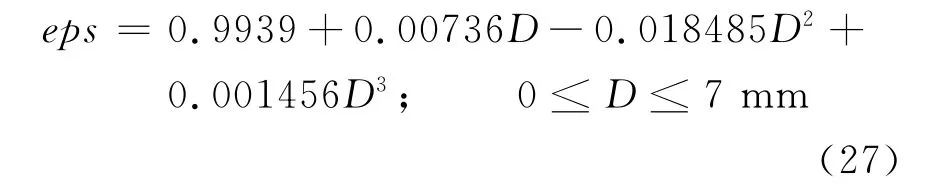
式中:eps=a／b代表軸比；D為橢球等體積球的直徑。a為長半軸長，b為短半軸長，eps＜1表示粒子為長橢球粒子，eps＞1表示粒子為扁橢球粒子，eps=1表示粒子為球形粒子。

圖6所示為橢球雨滴軸比與其等效半徑R的關系。所示的四種模型在對真實雨滴進行近似時，每一模型只有在某一特定雨滴直徑范圍上好于其它三者。參考圖7所示的不同大小雨滴的橫截面可以看出，當雨滴半徑小于0.675mm時，采用Keenan等人的模型，大于0.675mm小于2.2mm的雨滴采用Andsage等人的模型，其它值時采用Beard等人的模型。當雨滴變大以后，其形狀更加扁平。由軸比圖示可以知道，當雨滴等效直徑大于2.2mm時，Beard等人的模型的軸比值更小，這表明雨滴形狀更扁，更貼近實際情況。

在500mm×500mm×500mm空間內分布了500個隨機分布的橢球形降雨粒子，粒子的短半軸長b小于2mm.考慮軸比eps與等效球半徑R關系，采用Keenan等人的模型［15］建立降雨粒子模型。

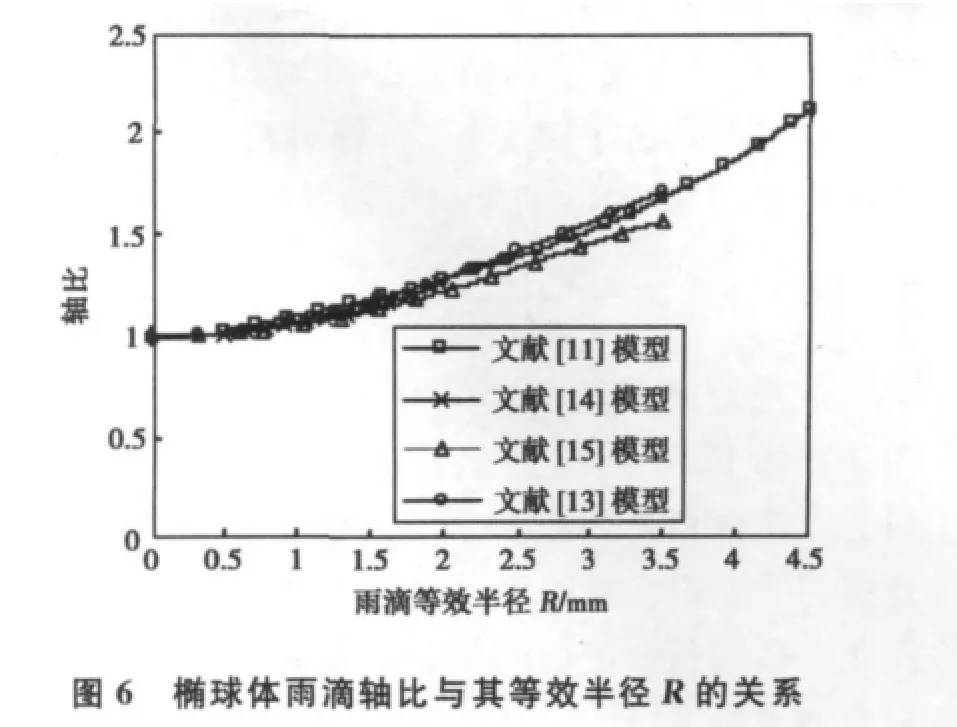
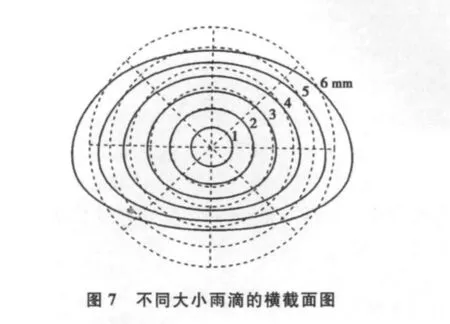
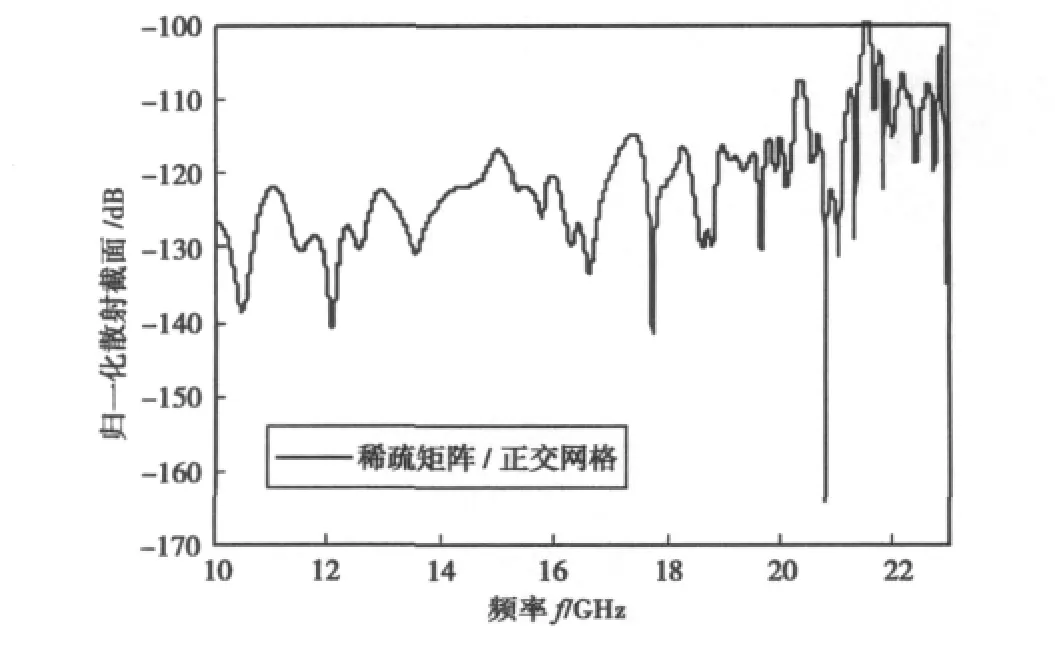
圖8 500mm×500mm×500mm空間內隨機分布500個半短軸0～2mm橢球形降雨群在不同頻段下的散射特性

對降雨模型進行剖分細化，未知量為27498.入射波入射方向與z軸夾θ=30°，φ=0°.在10～23 GHz的頻率范圍內每0.01GHz取一個采樣點，雨滴粒子的介電常數隨著頻率變化，介于4+0.04i和3.3495+0.105i之間，SMCG方法參數為:Ng=16，rmax=1.4Δrg和γ=2.圖8給出了隨機分布500個橢球形降雨群在不同頻段下的散射特性，散射角為0°，是前向散射。從圖中可以看出:在頻率較低時散射強度曲線變化比較緩慢，隨著工作頻率的提高，散射強度呈現明顯的抖動，且抖動幅度劇烈。這些都是由于頻率提高，降雨粒子電尺寸與波長可比擬，對電磁波的散射更加劇烈導致的。

3.結 論

從理論研究的角度出發，針對新一代星載降雨雷達新增K和Ka工作頻段測量的特點，對均勻／隨機分布的降雨雨團在K和Ka波段下的電磁散射特性進行了研究。從中可以看出，散射角較小時，降雨分布對散射特性的影響是可以忽略不計的，而當散射角較大時，這種分布因素的影響就必須加以考慮；隨著雷達工作波段的提高，粒子的電磁散射特性變化亦更加劇烈，對較小降雨進行測量具有較高的測量靈敏度，從而進一步提高星載降雨雷達探測中、高緯度地區小雨或小雪的能力。

綜上所述，新一代降雨雷達新增加K和Ka波段觀測，可以擴展降雨的檢測范圍，有助于區分不同類型的降雨，對提高星載降雨雷達測量精度具有重要的意義。

［1］KUMMEROW C，BARNES W，KOZU T.The tropical rainfall measuring mission（TRMM）sensor package［J］.Journal of atmospheric and oceanic technology，1998:809-817.

［2］KOZU T，KAWANISHI T，KUROIWA H，et al.Development of precipitation radar onboard the tropical rainfall measuring mission （TRMM）satellite ［J］.IEEE transactions on geoscience and remote sensing，2001，39（1）:102-116.

［3］唐治華，等.國外星載氣象雷達技術研究［J］.航天器工程.2008，17（5）:88-94.TANG Zhihua，DU Hui.Study on Overseas Spaceborne Meteorological Radar［J］.Spacecraft Engineering，2008，17（5）:88-94.（in Chinese）

［4］BARTON J P.Interal and near-surface electromagnetic fields for an absorbing spheroidal particle with arbitrary illumination［J］.Applied Optics，1995，34（36）:6471-8473.

［5］PURCELL E M，PENNYPACKER C R.Scattering and absorption of light by nonspherical dielectric grains［J］.Astrophys.J.，1973，186:705-714.

［6］WATERMAN P C.Symmetry，unitary，and geometry in electromagnetic scattering［J］.Phys Rev D，1971，3:825-839.

［7］丁大志，劉金權，胡云琴，等.基于多層快速多極子算法分析平面多層結構［J］.電波科學學報，2009，24（3）:422-426.DING Dazhi，LIU Jinquan，HU Yunqin，et al.Multilayered plane structure using multilevel fast multipole algorithm［J］.Chinese Journal of Radio Science，2009，24（3）:422-426.（in Chinese）

［8］孫玉發，陳志豪.分析三維隨機介質目標散射問題的SMCG方法［J］.中國科學技術大學學報，2003，33（3）:345-350.SUN Yufa，CHAN C H.Sparse matrix canonical grid method for scattering from 3Drandom dielectric scatterers［J］.Journal of University of Science and Technology of China，2003，33（3）:345-350.（in Chinese）

［9］CHAN C H.TSANG L..A sparse-matrix／canonical grid method for scattering by many scatterers［J］.Microwave Opt.Technol.Lett.，1995，8（2）:114-118.

［10］丁大志.復雜電磁問題的快速分析和軟件實現［D］.南京:南京理工大學，2007.

［11］PRUPPACHER H R，BEARD K V.A wind tunnel investigation of the internal circulation and shape of water drops falling at terminal velocity in air ［J］.The Quarterly Journal of the Royal Meteorological Society，1970，96（408）:247-256.

［12］石廣玉.大氣輻射學［M］.北京:科學出版社，2007.

［13］BEARD K V，CHUANG C.A new model for the equilibrium shape of raindrops.Journal of Atmospheric Sciences，1987，44（11）:1509-1524.

［14］ANDSAGER K，BEARD K V，LAIRD N F.Laboratory measurements of axis ratios for large raindrops.Journal of Atmospheric Sciences，1999，56（15）:2673-2683.

［15］KEENAN T D，CAREY L D ，ZRNIC D S，et al.Sensitivity of 5-cm wavelength polarimetric radar variables to raindrop axial ratio and drop size distribution.Journal of Applied Meteorology，2001，40（3）:526-545.