基于重構(gòu)時間采樣的空中機動目標檢測與參數(shù)估計
吳仁彪 王小寒 李 海 王冬梅
①(中國民航大學(xué)天津市智能信號與圖像處理重點實驗室 天津 300300)
②(中國民航西南地區(qū)空中交通管理局 成都 610202)
1 引言
機載預(yù)警雷達以高空飛行的飛機為載體,具有探測距離遠、覆蓋范圍大、機動靈活等特點。但由于它處于下視工作狀態(tài),面臨著比地基雷達更復(fù)雜的地(海)雜波問題,雜波不僅分布范圍廣,強度大,而且呈現(xiàn)空時 2 維耦合分布特性,從而導(dǎo)致目標常淹沒在強雜波背景中,檢測目標能力受到嚴重影響。STAP是一種有效的機載預(yù)警雷達地雜波抑制手段[1,2],但是傳統(tǒng)的STAP方法都是假設(shè)在相干處理時間(Coherent Processing Interval,CPI)內(nèi)目標回波多普勒頻率恒定。當(dāng)來襲目標具有很強的機動性時,其在一個CPI內(nèi)目標回波多普勒頻率隨時間發(fā)生變化,即發(fā)生多普勒走動,使得傳統(tǒng)的STAP方法相參積累性能大大下降,從而導(dǎo)致目標檢測能力下降[3]。
當(dāng)機動目標做勻加速運動時,目標回波信號為線性調(diào)頻(Linear Frequency Modulation,LFM)信號[4]。近年來,基于各種時頻分析工具的LFM信號的檢測與參數(shù)估計方法不斷出現(xiàn)[5-11],包括短時Fourier變換(STFT)[5,6],小波變換(WT)[5-7],Wigner-Ville分布(WVD)[5,6]和分數(shù)階Fourier變換(FRactional Fourier Transform,FRFT)[5,6,8-11]等。其中FRFT是1種廣義的傅里葉變換方法,它將信號分解在分數(shù)階傅里葉域的一組正交的chirp基上,這就給LFM信號的分析和處理帶來了可能性。同時FRFT是一種1維的線性變換,在檢測多個機動目標時它不會像WVD那樣產(chǎn)生交叉項,而且它的數(shù)值計算可借助FFT快速實現(xiàn),計算簡單,易于實現(xiàn),因此受到了廣泛重視。
將FRFT與STAP相結(jié)合為空中機動目標的參數(shù)估計提供了一條可能的途徑。但是,在地基雷達和合成孔徑雷達(Synthetic Aperture Radar,SAR)上利用FRFT來估計機動目標參數(shù)時都需要較多的脈沖點數(shù)[4,12,13],否則估計精度難以滿足要求。由于這個原因,上述方法難以直接應(yīng)用到機載預(yù)警雷達中,因為當(dāng)雷達脈沖重復(fù)頻率一定時,較多的脈沖點數(shù)意味著CPI加長,這會引起雜波和目標的距離走動,給后續(xù)處理帶來更大困難[1]。針對上述問題,本文利用干涉SAR中相位展開的思想[14],提出了基于重構(gòu)時間采樣的空中機動目標檢測和參數(shù)估計方法,該方法利用空間采樣來重構(gòu)時間采樣,等效于增加了單個陣元的時間采樣點數(shù),可以提高參數(shù)估計精度。仿真實驗的結(jié)果證明了該方法的有效性。
2 數(shù)據(jù)模型和問題描述
本文首先給出雷達接收到的數(shù)據(jù)形式。設(shè)機載平臺上沿航向方向放置N元均勻線陣,陣元間距為d=0 .5λ,λ為雷達發(fā)射脈沖波長,一個CPI內(nèi)發(fā)射K個脈沖。假定單個距離門內(nèi)最多存在一個目標,則待檢測單元的空時快拍可寫成
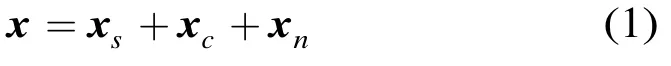
其中xs,xc和xn分別表示目標、雜波和噪聲成分。雜波和噪聲數(shù)據(jù)的具體模型見參考文獻[3]。
xs表示目標,可表示為如下形式
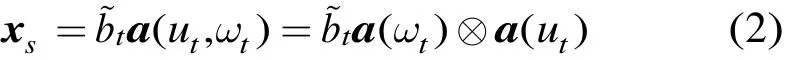
其中為目標回波復(fù)幅度,a()為目標空時導(dǎo)向矢量,?表示Kronecker積,時域?qū)蚴噶縜(ωt)=[1,ej2π?1?fd/fr,…,ej2π?(K- 1)?fd/fr]T 為K×1維列向量,空域?qū)蚴噶縜(ut)=[1,ej2π?1?dcosψt/λ,…,ej2π?(N-1)?dcosψt/λ]T為N×1維列向量,ψt表示目標來向角,fd表示多普勒頻率, (?)T表示轉(zhuǎn)置運算。
當(dāng)目標做勻加速直線運動時,只有目標回波的多普勒頻率發(fā)生了變化[3]
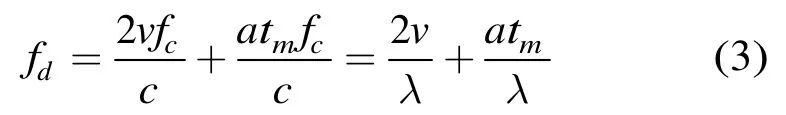
tm表示慢時間,fc為載波頻率,v為目標的初始速度,a為目標的加速度,將fd代入到a(ωt)中得到勻加速目標的時域?qū)蚴噶繛?/p>
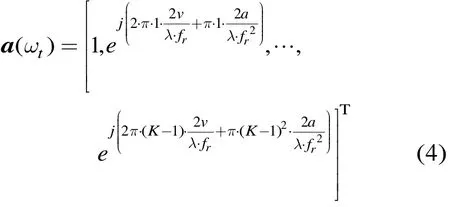
可見,勻加速目標的時域?qū)蚴噶坎糠钟蓛刹糠纸M成,分別為目標初始多普勒頻率項和調(diào)頻率項,即當(dāng)目標做勻加速直線運動時,目標的回波信號為LFM信號。
由雜波分布特性[2]可知:雜波分布范圍廣,強度大,并且呈現(xiàn)出很強的空時耦合特性,在很大程度上淹沒了目標信號,嚴重影響了雷達對目標信號參數(shù)的估計性能。因此,本文的工作可歸結(jié)為對強雜波背景下的LFM信號的檢測和參數(shù)估計。
3 空間采樣重構(gòu)時間采樣方法
由文獻[9]可知,F(xiàn)RFT是一種有效的LFM信號檢測和參數(shù)估計工具。但是,直接將FRFT應(yīng)用到機載預(yù)警雷達中會產(chǎn)生估計精度較差的問題。基于此,本文利用干涉SAR中相位展開的思想[14],提出了一種重構(gòu)時間采樣的參數(shù)估計方法,即對空間多陣元數(shù)據(jù)補償相應(yīng)相位后進行首尾拼接,該方法等效于增加了單個陣元的時間采樣點數(shù),可實現(xiàn)對多個陣元數(shù)據(jù)的相干積累,提高參數(shù)估計精度。本節(jié)將從重構(gòu)時間采樣、構(gòu)造代價函數(shù)、解模糊和算法步驟4個部分來重點介紹重構(gòu)時間采樣方法的具體實施過程。
3.1 重構(gòu)時間采樣
當(dāng)目標做勻加速運動時,對于機載預(yù)警雷達的每個陣元來說其回波信號均為一個LFM信號(雜波抑制后),且每個陣元的LFM信號只差空間相位,如圖1(a)所示。因此可以對空間中每個陣元的數(shù)據(jù)進行相位補償后首尾拼接,使其等效為增加單個陣元時間采樣點數(shù)的效果,如圖1(b)所示。不失一般性,下面以兩個陣元為例討論將多陣元首尾拼接時每個陣元所需補償?shù)南辔弧?/p>
由第2節(jié)的目標數(shù)據(jù)模型可知,當(dāng)不考慮空間相位時,兩個陣元接收到的目標數(shù)據(jù)為
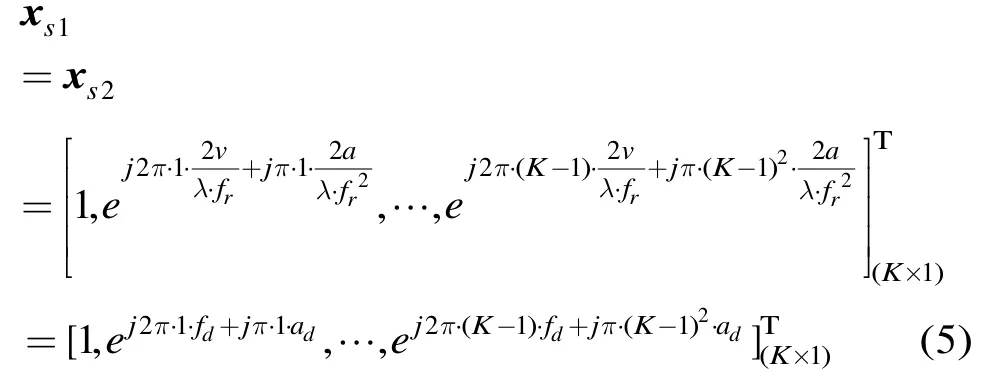
其中xs1表示第1個陣元接收到的目標信號,xs2表示第2個陣元接收到的目標信號,K為脈沖點數(shù),fd=2v/λfr為初始頻率,ad=2a/λfr2為調(diào)頻率,λ為波長,fr為脈沖重復(fù)頻率。
當(dāng)一個陣元的時間采樣點數(shù)由K增加到2K時,該陣元接收到的目標信號為

其中⊙為Hadamard積。由此可見,對第2個陣元的數(shù)據(jù)進行相位補償后再跟第1個陣元的數(shù)據(jù)拼接就可以等效為一個陣元直接增加時間采樣點數(shù)的效果。
由式(6)可以得出對第2個陣元應(yīng)該補償?shù)南辔粸?/p>
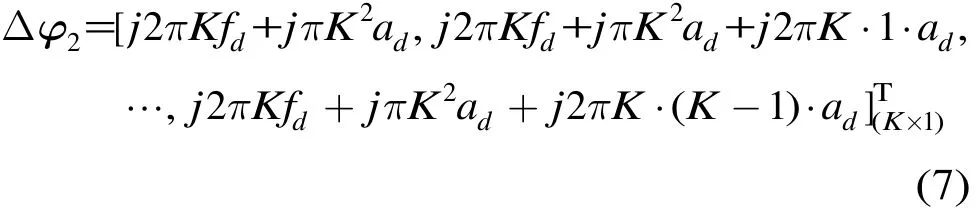
同理,第n個陣元應(yīng)該補償?shù)南辔粸?/p>
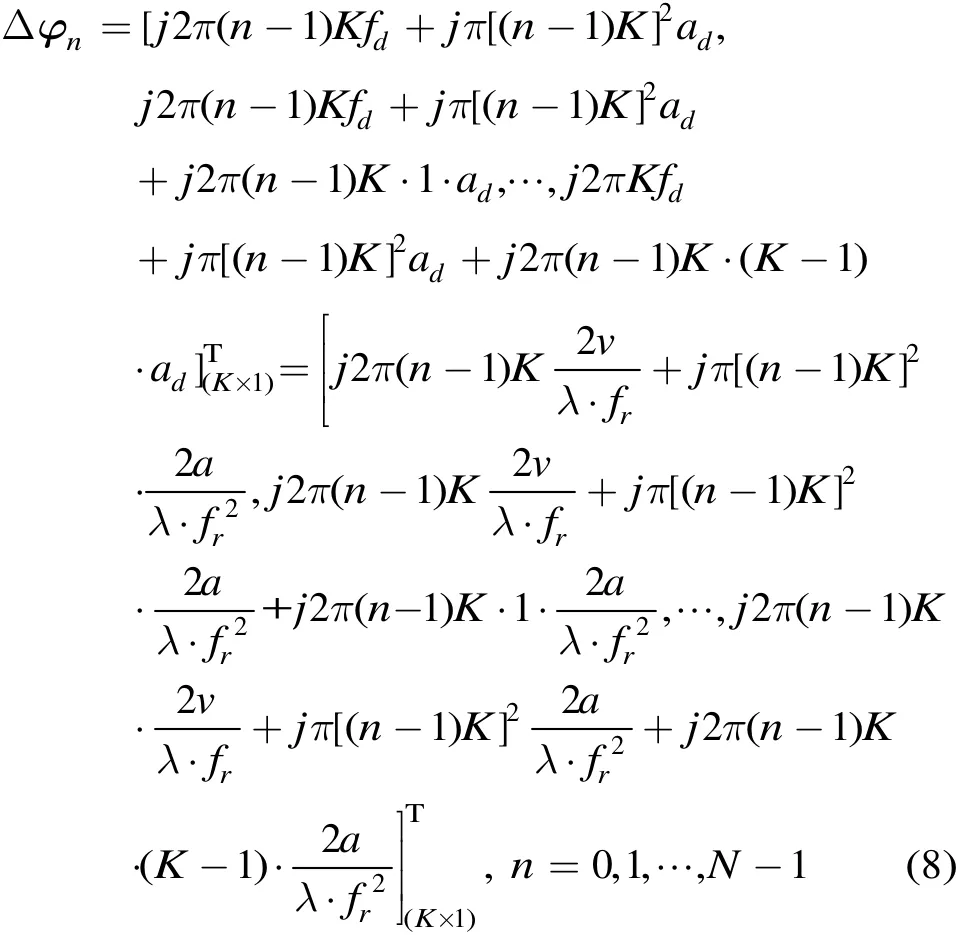
這樣,將每個陣元接收到的數(shù)據(jù)分別補償其相對應(yīng)的相位(參考陣元除外)后進行首尾拼接,此時再進行FRFT變換,相當(dāng)于對所有數(shù)據(jù)進行相干積累,因此積累后的目標能量大大提高,估計精度更好。
3.2 構(gòu)造代價函數(shù)
然而,由上述分析可知:每個陣元所需補償?shù)南辔恢杏职宋粗哪繕藚?shù),導(dǎo)致無法直接對多個陣元進行數(shù)據(jù)拼接。由于FRFT是線性變換,能夠?qū)FM信號進行能量積累,因此可以構(gòu)造一個參數(shù)搜索區(qū)間,對此區(qū)間內(nèi)的每組參數(shù)進行多陣元拼接后做FRFT變換,當(dāng)拼接效果最好時能量積累最大,所以取每組參數(shù)拼接后數(shù)據(jù)做FRFT變換后的能量最大值作為代價函數(shù),只需通過搜索代價函數(shù)的最大值就可以得到參數(shù)的估計結(jié)果。為減小計算量,本文對拼接后的數(shù)據(jù)進行Zoom-FRFT變換[15],即根據(jù)需要選擇變換輸出的局部譜區(qū)域,求得變換后的能量最大值。Zoom-FRFT變換縮短了2維搜索的區(qū)域,因此減小了計算量。所以,在參數(shù)搜索區(qū)間內(nèi)構(gòu)造代價函數(shù)為
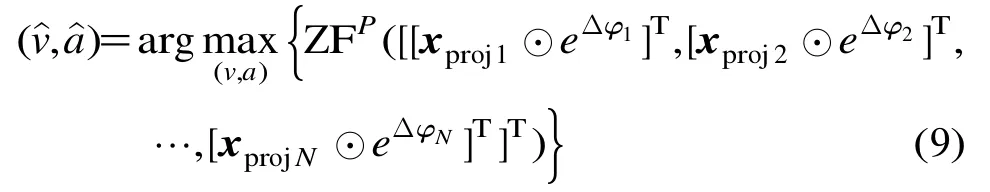
其中xprojn為第n個陣元雜波抑制后數(shù)據(jù),Δφn為第n個陣元所需補償?shù)南辔唬娛?8),[[xproj1⊙個陣元數(shù)據(jù)進行重構(gòu)時間采樣(NK×1維列向量),ZFP[?]為Zoom-FRFT的算子符號。這樣當(dāng)搜索到目標真值時,陣元拼接效果最好,能量積累最大,所以求其峰值對應(yīng)的參數(shù)即為目標參數(shù)(證明略)。
3.3 解模糊方法
但是由式(8)可以看出:每個陣元所需的補償項存在周期性變化,這樣就導(dǎo)致估計結(jié)果會產(chǎn)生模糊,因此需要對其進行解模糊處理,進一步精確參數(shù)搜索區(qū)間。不失一般性,以兩個陣元為例具體分析估計結(jié)果產(chǎn)生模糊原因以及解模糊方法。
首先以單頻信號為例,即加速度項為零,此時第2個 陣 元 應(yīng) 該 補 償 的 項 為[ej2πKfd,ej2πKfd,…,,對初始速度進行搜索,其代價函數(shù)如圖2所示,正是由于補償項ej2πfd K為一個周期函數(shù),導(dǎo)致參數(shù)搜索的代價函數(shù)也會呈現(xiàn)周期性變化,其周期滿足:=2v?K/λfr=N,即速度非模糊最小周期為vp=λfr/(2K),帶來的結(jié)果就是如果不能正確地確定搜索區(qū)間,就有可能搜索到其他區(qū)間的峰值,產(chǎn)生模糊,導(dǎo)致誤差很大,所以就要對其進行解模糊。
當(dāng)估計結(jié)果產(chǎn)生模糊時,模糊值和真值的關(guān)系為
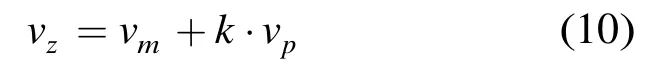
其中vz為理論真值,vm為搜索到的模糊值,vp為周期,k為整數(shù)。由于其周期性由K決定,所以可以通過取不同的K值來解模糊,如式(11)表示
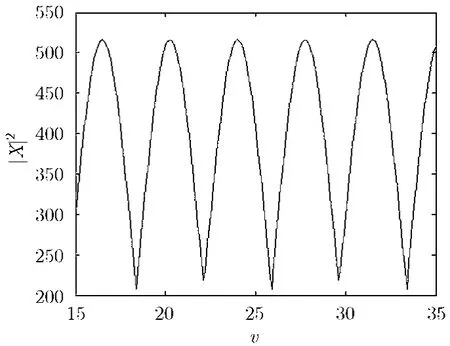
圖2 初始速度參數(shù)搜索代價函數(shù)示意圖
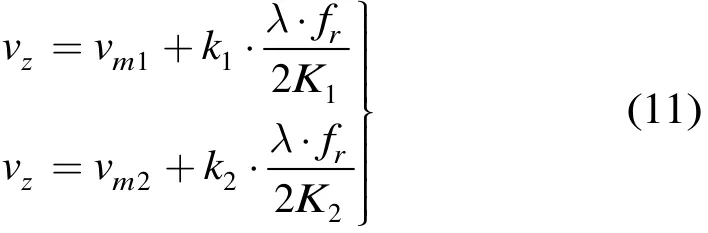
通過取不同的K值,求解此方程組,k1,k2取整數(shù),即可求得vz,確定理論真值所在的區(qū)間。
當(dāng)含有加速度時,第2個陣元的補償項為
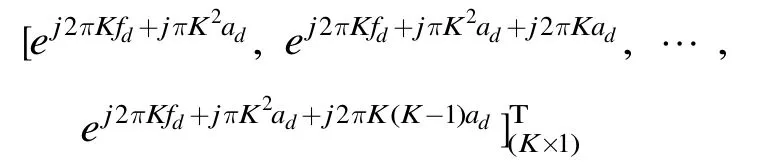
3.4 算法步驟
圖3為本文所提基于重構(gòu)時間采樣方法估計機動目標參數(shù)的流程圖。具體步驟如下:
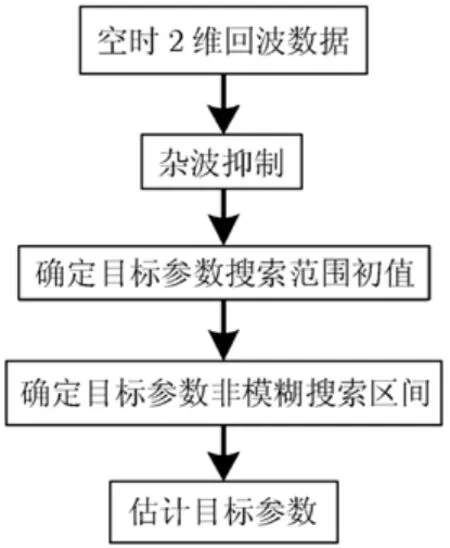
圖3 本文方法實現(xiàn)框圖
第1步 雜波抑制 本文通過子空間投影技術(shù)進行雜波抑制,詳細過程在此不再敘述,請參考文獻[16]中步驟1。
第2步 確定目標參數(shù)搜索范圍初值 由第1步可知,雜波抑制后的數(shù)據(jù)可表示為

分別對雜波抑制后的每個陣元數(shù)據(jù)進行FRFT變換,然后再對結(jié)果進行非相干積累,如式(13)所示。
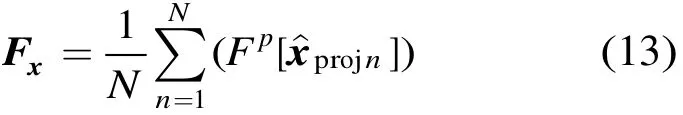
其中為利用估計協(xié)方差矩陣抑制雜波后第n個陣元的數(shù)據(jù),N為陣元數(shù)。
搜索得到非相干積累能量最大時的速度和加速度為
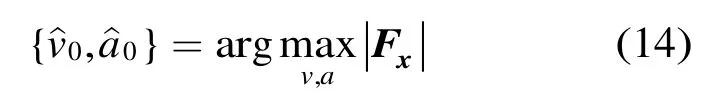
該步搜索參數(shù)的初值也可通過快速解線調(diào)的方法來確定[3]。
第3步 確定目標參數(shù)非模糊搜索范圍 由4.3節(jié)的分析可知,需要對參數(shù)搜索范圍進行解模糊處理。選取不同的脈沖采樣點數(shù)K1和K2,確定一個參數(shù)搜索范圍,初始速度的搜索范圍取5倍于其非模糊周期的范圍,加速度的搜索范圍可根據(jù)先驗信息選取,如空空導(dǎo)彈已經(jīng)可以達到100g的機動過載,F(xiàn)-22戰(zhàn)斗機也有5g以上的超音速機動能力等[4]。通過式(9)分別估計結(jié)果和,再根據(jù)式(11)來進行解模糊處理
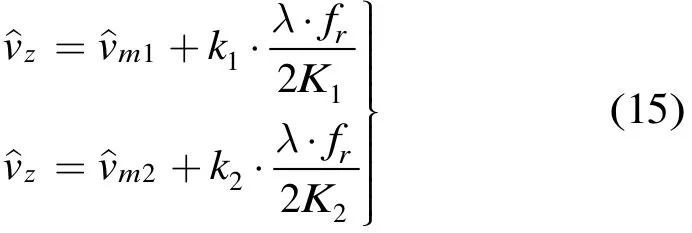
第4步 估計目標參數(shù) 此時再根據(jù)式(9)在第3步得到的參數(shù)非模糊搜索范圍內(nèi)構(gòu)造代價函數(shù)
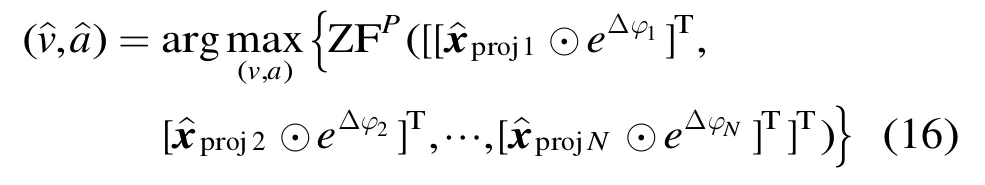
求得代價函數(shù)最大值所對應(yīng)的參數(shù),即可得到估計結(jié)果。
4 仿真分析
仿真參數(shù)設(shè)置:天線陣為陣元數(shù)N=16的正側(cè)視理想均勻線陣,陣元間距d=0.5λ。載機速度為120 m/s,雷達工作波長為0.32 m,平臺高度為10 km,雷達距離分辨率為20 m,脈沖重復(fù)頻率為1500 Hz,相干處理脈沖數(shù)K=64,輸入信噪比SNR=0 dB,雜噪比CNR=50 dB。機動目標處于檢測單元內(nèi),處于方位角90°處,初始速度為24.01 m/s,加速度為299.9 m/s,實驗中假設(shè)目標方位已知,該實驗中估計參數(shù)均方根誤差均進行了200次蒙特卡羅實驗。
圖4所示為雜波抑制前的功率譜,由于信雜比很低,信號完全被淹沒在雜波中。圖5為雜波抑制后的功率譜,可以看出雜波被抑制掉了,目標突顯出來,由于目標存在加速度,其在多普勒域存在一定的展寬。
圖6為不同方法能量積累效果圖,圖6(a)為對單個陣元進行FRFT變換的結(jié)果,圖6(b)為對每個陣元的數(shù)據(jù)進行FRFT變換后進行非相干積累的結(jié)果,圖6(c)為利用本文方法處理后進行FRFT的結(jié)果。通過比較可以看出,圖6(a)中由于只利用了單個陣元的數(shù)據(jù)進行變換,所利用脈沖點數(shù)較少,因此積累后目標能量很微弱,在圖中很難檢測到目標。圖6(b)中雖然利用了多個陣元的數(shù)據(jù),但由于是非相干積累,因此改善能力有限,仍然無法對目標進行很好的檢測。圖6(c)中由于利用空間采樣來重構(gòu)時間采樣的方法拼接等效成一個陣元的數(shù)據(jù)后進行FRFT變換,相當(dāng)于利用多個陣元的數(shù)據(jù)進行相干積累,因此積累后的目標能量大大提高,能夠很好地進行目標檢測和估計。
不同方法估計結(jié)果的均方根誤差如表1所示,可見本文方法的參數(shù)估計結(jié)果精度最高。
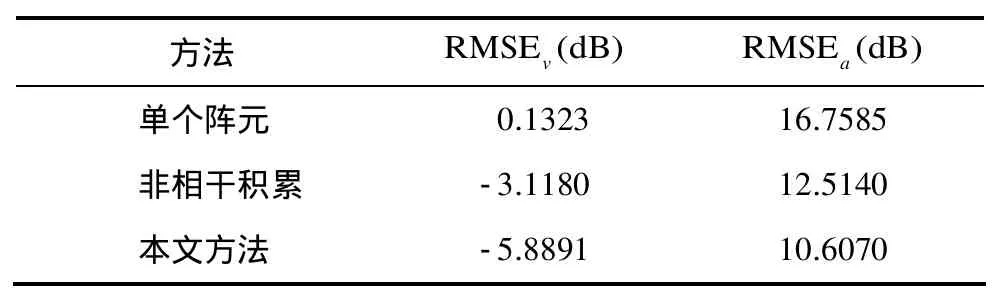
表1 不同方法估計結(jié)果比較表
圖7為3種方法估計得到的參數(shù)均方根誤差與CRB界的比較結(jié)果圖(機載雷達機動目標參數(shù)估值的CRB推導(dǎo)過程略),其中圖7(a)為初始速度均方根誤差與CRB界的比較結(jié)果圖,圖7(b)為加速度均方根誤差與CRB界的比較結(jié)果圖。可以看出本文方法估計性能最接近CRB界,估計效果最好,尤其在低信噪比的情況下,其優(yōu)勢更加明顯。
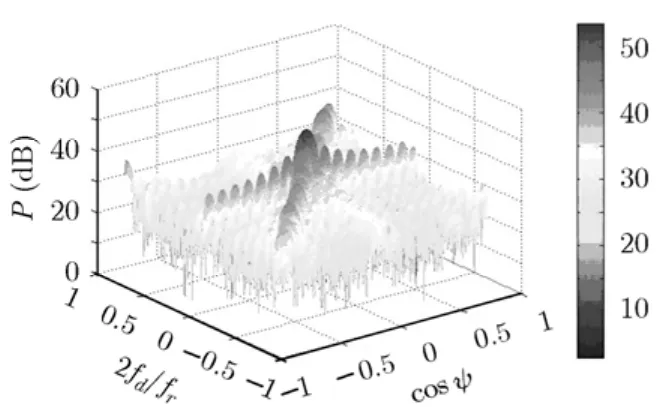
圖4 總回波的功率譜
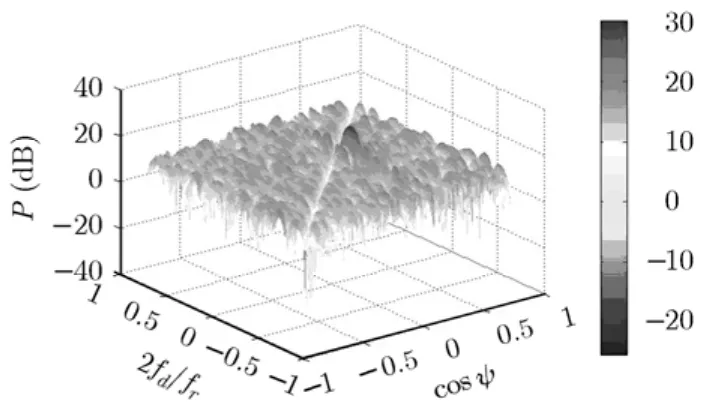
圖5 雜波抑制后的功率譜
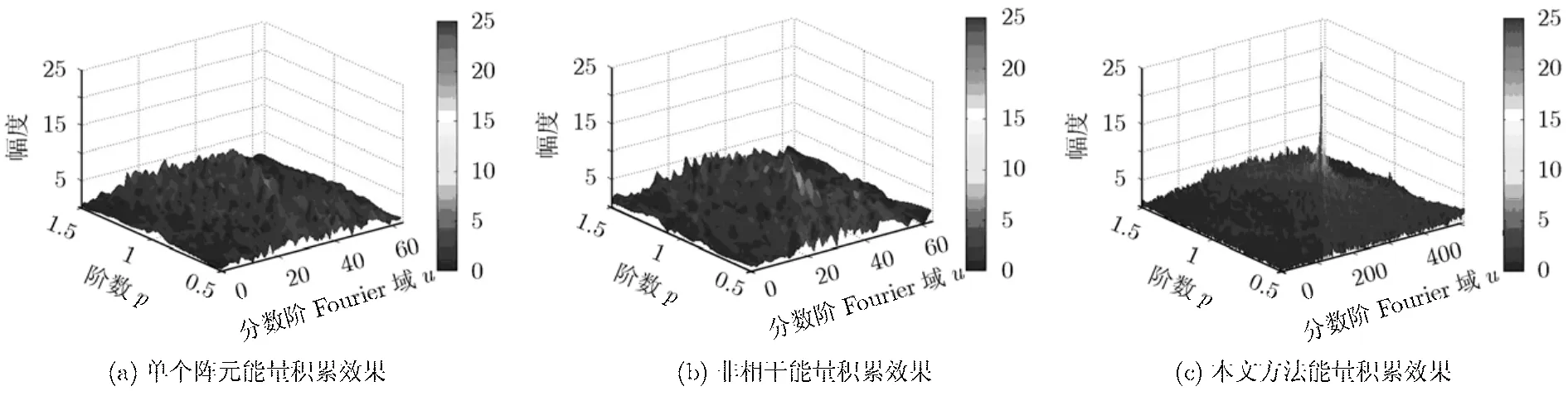
圖6 不同方法能量積累效果圖
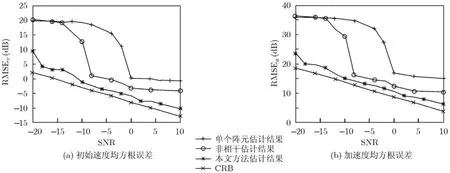
圖7 參數(shù)均方根誤差隨信噪比變化曲線
表2給出了本文算法中各個步驟所需運算量,其中Ns為估計協(xié)方差矩陣所需樣本數(shù),prg表示做FRFT變換時階數(shù)p的搜索范圍[pc,pz],pc和pz為該范圍的初值和終值,Δp為階數(shù)p的搜索步長,vrg表示初始速度的搜索范圍[vc,vz],vc和vz為該范圍的初值和終值,Δv為初始速度搜索步長,arg表示加速度的搜索范圍[ac,az],ac和az為該范圍的初值和終值,Δa為加速度搜索步長,K1和K2為解模糊時選取的不同脈沖點數(shù),Nc為該方法中所需拼接的陣元數(shù)。
5 結(jié)束語
本文提出了一種基于重構(gòu)時間采樣的空中機動目標檢測和參數(shù)估計方法,該方法能夠在脈沖點數(shù)有限的情況下得到準確的目標參數(shù)估計結(jié)果。文中將該方法的估計結(jié)果與直接應(yīng)用FRFT變換的估計結(jié)果進行了比較,同時給出了其與CRB界比較的結(jié)果,可以看出,該方法的估計性能較之其它方法有了顯著的提高。

表2 本文算法中各個步驟所需運算量分析結(jié)果
[1]Klemm R.Principle of Space-Time Adaptive Processing[M].3rd Edition,UK,IET Publishers,2006: 1-100.
[2]王永良,彭應(yīng)寧.空時自適應(yīng)信號處理[M].北京: 清華大學(xué)出版社,2000: 26-45.Wang Yong-liang and Peng Ying-ning.Space-Time Adaptive Processing[M].Beijing: Tsinghua University Press,2000:26-45.
[3]王冬梅.基于STAP的空中機動目標檢測研究[D].[碩士論文],中國民航大學(xué),2010.Wang Dong-mei.Study on space time adaptive maneuvering target detection technology[D].[Master dissertation],Civil Aviation University of China,2010.
[4]劉建成.加速運動目標檢測及跟蹤技術(shù)研究[D].[博士論文],國防科學(xué)技術(shù)大學(xué),2007.Liu Jian-cheng.Study on accelerating target detection and tracking[D].[Ph.D.dissertation],National University of Defense Technology,2007.
[5]張賢達,保錚.非平穩(wěn)信號分析與處理[M].北京: 國防工業(yè)出版社,1998: 12-284.Zhang Xian-da and Bao Zheng.Analysis and Processing of Nonstationary Signal[M].Beijing: National Defense Industrial Press,1998: 12-284.
[6]唐向宏,李齊良.時頻分析與小波變換[M].北京: 科學(xué)出版社,2008: 45-136.Tang Xiang-hong and Li Qi-liang.Time-Frequency Analysis and Wavelet Transform[M].Beijing: Science Press,2008:45-136.
[7]Li Liang-chuan.A new method of wavelet transform based on FFT for signal processing[C].WRI Global Congress on Intelligent Systems,Wuhan,2010: 203-206.
[8]Pei Soo-chang and Ding Jian-jiun.Fractional Fourier transform,Wigner distribution,and filter design for stationary and nonstationary random processes[J].IEEE Transactions on Signal Processing,2010,58(8): 4079-4092.
[9]陶然,鄧兵,王越.分數(shù)階傅里葉變換以及應(yīng)用[M].北京: 清華大學(xué)出版社,2009: 12-49.Tao Ran,Deng Bing,and Wang Yue.Fractional Fourier Transform and Its Applications[M].Beijing: Tsinghua University Press,2009: 12-49.
[10]Qi Lin,Tao Ran,Zhou Si-yong,et al..Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J].Science in China Ser.F Information Sciences,2003,33(8): 749-759.
[11]Zhao Fen-xia and Zhai Xin-duo.The algorithm and error analysis of fractional Fourier transform[C].International Conference on Information Engineering and Computer Science,Wuhan,2010: 1-4.
[12]孫泓波,顧紅,蘇衛(wèi)民,等.利用分數(shù)階Fourier域濾波的機載SAR多運動目標檢測[J].航空學(xué)報,2002,23(1): 33-37.Sun Hong-bo,Gu Hong,Su Wei-min,et al..Using the filtering in fractional Fourier domain for airborne SAR multiple moving targets detection[J].Acta Aeronautica Et Astronautica Sinica,2002,23(1): 33-37.
[13]胡海榮.基于分數(shù)階Fourier變換的合成孔徑雷達動目標檢測方法[D].[碩士論文],浙江工業(yè)大學(xué),2009.Hu Hai-rong.The SAR moving targets detection based on fractional Fourier transform[D].[Master dissertation],Zhejiang University of Technology,2009.
[14]李海,廖桂生.對配準誤差穩(wěn)健的多基線相位展開方法[J].電子學(xué)報,2008,36(9): 1670-1675.Li Hai and Liao Gui-sheng.A robust phase unwrapping method to coregistration error for multiba seline InSAR systems[J].Acta Electronca Sinica,2008,36(9): 1670-1675.
[15]趙興浩,陶然,鄧兵,等.分數(shù)階傅里葉變換的快速計算新方法[J].電子學(xué)報,2007,35(6): 1089-1093.Zhao Xing-hao,Tao Ran,Deng Bing,et al..New methods for fast computation of fractional Fourier transform[J].Acta Electronca Sinica,2007,35(6): 1089-1093.
[16]吳仁彪,賈瓊瓊,李海.機載雷達高速空中微弱動目標檢測新方法[J].電子與信息學(xué)報,2011,33(6): 1459-1464.Wu Ren-biao,Jia Qiong-qiong,and Li Hai.Detection of fast moving dim targets on airborne radar via STAP[J].Journal of Electronics&Information Technology,2011,33(6):1459-1464.

