斜腿剛構橋模型試驗研究

陸瀟雄 劉偉星 郁文杰 李銳 張靜

(蘇州科技學院天平學院，江蘇 蘇州 215011)

斜腿剛構橋是近些年發展起來的一種橋型［1］，因其具有呈水平方向的梁式結構和呈斜向的支撐結構，在力學行為上兼具梁式剛構特性和拱的特性，呈現出良好的力學性能，在橋型構造上以少量構件和簡單明了的幾何圖形構成簡練的橋梁形態，有一種簡潔而生動，纖細而有力的橋梁美學效應。［2－3］

目前，國內針對斜腿剛構橋的結構、力學特性及構造形式等進行了一些研究，如，楊軍猛等［4］結合有限元對斜腿剛構橋進行了力學性能分析，劉世忠［5］對斜腿剛構橋進行了整體模型試驗，仇祚禮等［6］對斜體剛構橋進行了三維實體有限元分析。但是這些研究皆是基于箱型截面的斜腿剛構橋進行的，未涉及板式截面的斜腿剛構橋。因此，為了弄清該類橋梁結構的整體受力特性，本文以某座斜腿剛構橋為工程實例，在其基礎上進行了有機玻璃縮尺模型試驗及有限元分析。

1 試驗

1.1 模型制作

由于有機玻璃材料與一般彈性理論的基本假定基本一致，故選取有機玻璃為材料制作模型。

有機玻璃屬于脆性材料，對缺口有敏感性，在應力下易開裂，因此對模型加工工藝提出了較高的要求，同時為了保證模型整體的受力性能，采用機加工方法使模型一體成型，制作模型如圖1所示，其相關參數如表1所示。

圖1 模型制作圖

表1 有機玻璃的材料參數

模型按1∶100幾何縮尺進行設計，模型全長37.6 cm，寬8 cm，跨徑布置為11.3 cm+15 cm+11.3 cm，橋型整體為板型，橋面截面尺寸為11 mm×80 mm(高×寬);斜腿處界面尺寸為15 mm×80 mm(高×寬)，如圖2所示。斜腿與板橋銜接處采用二次拋物線變化，并且斜腿與鋼梁底座的凹槽鑲嵌，同時在其鑲嵌處填充環氧樹脂AB膠固結，橋臺與懸臂端之間用橡膠墊作為支座。

圖2 模型尺寸(mm)

1.2 測點布置

根據模型結構的對稱性，測試截面布置在跨中截面(A－A)、橋面與斜腿連接部位(B－B)、斜腿底部(C－C)。根據截面的受力情況，采用縱向應變片測試截面的應力，測點布置如圖3所示。跨中截面撓度采用百分表測試。

1.3 試驗過程

為了提供所需的荷載和穩定的加載力，同時考慮測試系統應具有穩定性好、抗干擾能力強、可靠性高等特性，故采用SX3501C測力儀來得到穩定的荷載輸出。

圖3 橫斷面應變測點布置圖

試驗加載工況為跨中單點加載，加載方式如圖4所示。試驗以每級0.2 kN增量逐級加載，加載等級為Ⅴ級，分別為0.2 kN、0.4 kN、0.6 kN、0.8 kN、1.0 kN。加載前，先對模型進行0.2 kN的預加載，消除非線性彈性變形后，再進行逐級加載，確保模型始終處于彈性變形階段。

圖4 試驗加載方式

2 有限元模型分析

通過使用Midas有限元分析軟件，建立梁單元模型，如圖5所示，模型共劃分為553個節點，567個單元。為確保加載過程中斜腿底部不發生位移，模型的斜腿底部設置為固結，懸臂端部僅施加了豎向約束，其有限元分析結果如圖6所示(僅給出加載等級為1 kN時有限元分析結果)。

圖5 Midas建模模型

6 在1 kN荷載作用下有限元分析結果

3 結果對比

3.1 理論計算

采用力法對模型結構的控制截面求出應力，同時利用圖乘法計算出模型結構的跨中撓度。其計算方法是建立在模型為等截面的桿件結構基礎上，并認為材料為均勻、連續、各向同性的可變性固體來進行計算的。計算所得出的應力與撓度見表2所示。

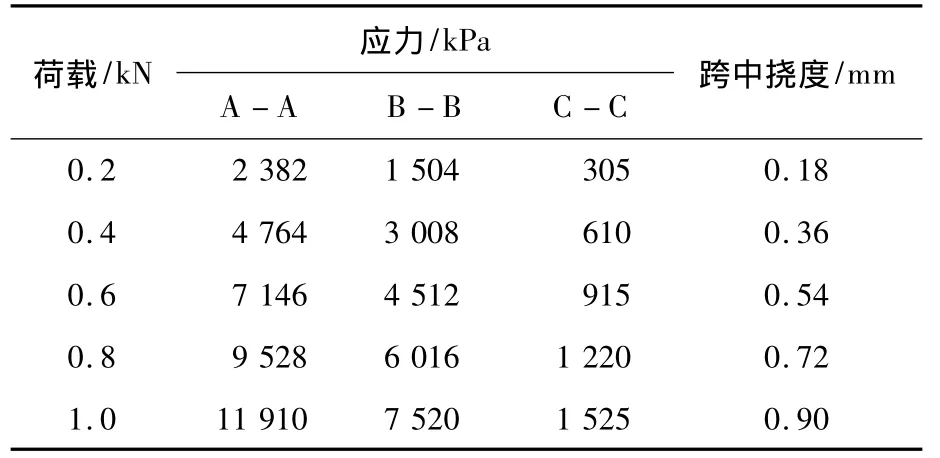
表2 理論計算值

3.2 對比分析

3.2.1 跨中的拉應力

跨中截面(A－A)拉應力的計算值、試驗值及有限元分析值如表3所示，拉應力隨荷載變化曲線如圖7所示。從表3與圖7可以明顯看出，實測值、計算值及有限元分析值三者隨荷載變化規律一致。各級荷載作用下實測值最小，計算值最大。其主要原因是由于在計算時忽略了模型梁墩固結處的板厚變化。

實測值相對于計算值的偏差較大，平均為17.52%，而實測值相對于有限元分析值的偏差較小，平均為7.14%，由此說明將模型梁墩固結處變截面近似等截面計算，其對計算結果有一定的影響。

表3 荷載作用下跨中截面拉應力

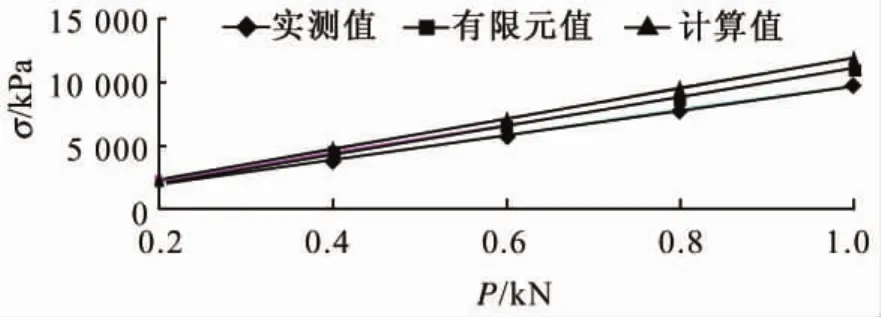
圖7 跨中拉應力隨荷載變化曲線

跨中(A－A)截面撓度對比結果如表4所示，撓度隨荷載變化曲線如圖8所示。從表4與圖8可以看出，跨中截面撓度隨荷載的變化規律與跨中截面拉應力變化規律相同，進一步說明在計算時忽略梁墩固結處的截面尺寸變化會導致計算偏差較大。

3.2.2 跨中的撓度

表4 荷載作用下跨中截面撓度值

圖8 跨中撓度隨荷載變化曲線

實測值相對于計算值的偏差較大，平均為14.93%，而有限元分析值相對于計算值的偏差較小，平均為5.56%。

3.2.3 斜腿頂截面的拉應力

斜腿頂截面(B－B)拉應力的計算值、試驗值及有限元分析值如表5所示，拉應力隨荷載變化曲線如圖9所示。表5、圖9顯示，實測值、計算值及有限元分析值三者隨荷載變化的規律性基本一致。各級荷載作用下實測值最小，計算值最大，實測值和有限元分析值小于計算值的主要原因是斜腿頂處是應力集中區，實際粘貼應變片時，粘貼點位的精度不能得到保證，導致與測試截面不能吻合，對實測值產生一定的影響。

實測值相對于計算值的偏差較大，平均為14.61%，而有限元分析值相對于計算值的偏差較小，平均為7.11%，說明有限元分析值與計算值所計算截面相吻合，與測試截面不相符合。

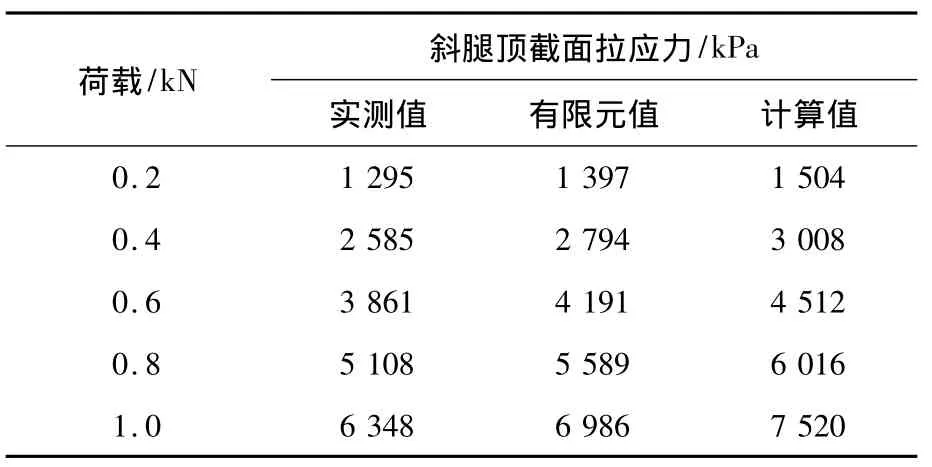
表5 荷載作用下斜腿頂截面拉應力

圖9 斜腿頂部拉應力隨荷載變化曲線

3.2.4 斜腿底截面的拉應力

斜腿底截面(C－C)拉應力的計算值、試驗值及有限元分析值如表6所示，拉應力隨荷載變化曲線如圖10所示。從表6與圖10可以看出，實測值、計算值及有限元分析值三者隨荷載變化規律基本一致。其拉應力計算值最大，實測值最小，而實測值和有限元分析值小于計算值，主要原因是斜腿剛構橋模型結構為超靜定結構，較小位移能導致較大應力，而制作模型的精度存在一定的偏差，故在斜腿與鋼梁底座凹槽鑲嵌時造成一定的裝配應力，致使偏差較大。

實測值相對于計算值的偏差較大，平均為19.62%，而有限元分析值相對于計算值的偏差較小，平均為9.18%，說明實際模型制作的精度對試驗產生較大的影響。

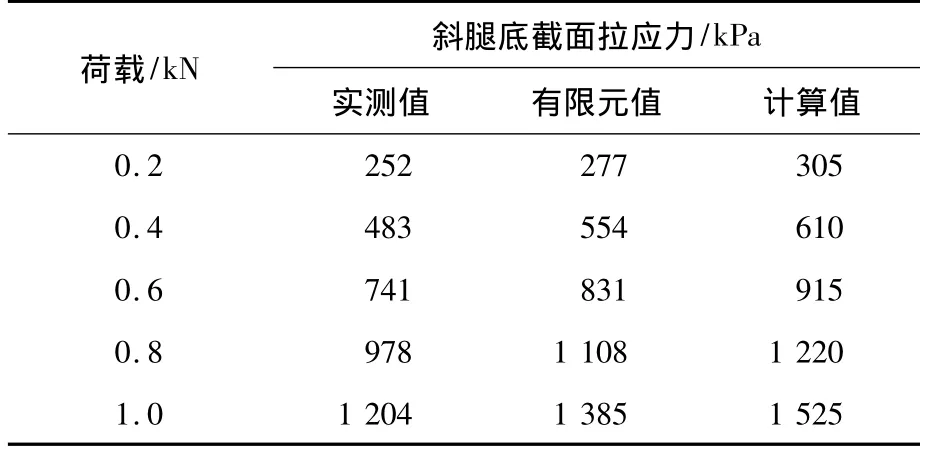
表6 荷載作用下斜腿底截面拉應力

圖10 斜腿底部拉應力隨荷載變化曲線

綜上所述，彈性階段的試驗值與有限元分析值及計算值吻合較好。

4 關鍵參數對撓度的影響

分跨比及斜腿傾斜角度是斜腿剛構橋結構設計時要考慮的重要參數，為了進一步優化斜腿剛構橋結構設計，可通過有限元模型模擬分跨比、斜腿傾斜角度結構撓度的影響。

為了得到同等的比較條件，在模擬時進行了如下假設和規定:

1)結構分析時，始終保證跨中跨徑L2=15 cm，邊跨跨徑與跨中跨徑比L1/L2=0.6～0.8，等值0.05變化。

2)分跨比不同時，結構的截面尺寸、荷載等參數均相同，保持不變。

3)斜腿傾斜角度變化范圍為30°～60°，等值5°變化。

4)斜腿傾斜角度不同時，結構的截面尺寸、荷載等參數均相同，保持不變。

4.1 分跨比對撓度的影響

保持其他參數不變，僅改變分跨比，分跨比分別設計為 0.6、0.65、0.70、0.75、0.8，跨中截面撓度及斜腿頂截面撓度隨分跨比的變化曲線如圖11所示。圖11顯示，當分跨比從0.60增加到0.65時，模型截面撓度呈減小趨勢，且下降段較陡;當分跨比增至0.65后撓度曲線出現轉折點，模型截面撓度呈增加趨勢，但上升較緩。

圖11 分跨比對撓度的影響

圖11中跨中截面及斜腿頂截面的撓度變化規律皆是隨著分跨比增大，呈先減后增趨勢，分跨比增至0.7時，其撓度值基本趨近于一定值。因此，在斜腿剛構橋結構設計時其分跨比為0.65～0.75時較為合理。

4.2 斜腿傾斜角度對撓度的影響

保持其他參數不變，僅改變斜腿傾斜角度，斜腿傾斜角度分別設計為 60 °、55 °、50 °、45 °、40°、35°、30°。跨中截面撓度及斜腿頂截面撓度隨傾斜角度的變化曲線如圖12所示。圖12中曲線變化表明，當斜腿傾斜角度從60°減小至45°時，模型截面撓度呈上升趨勢，且上升較緩。當斜腿傾斜角度減至45°后撓度曲線出現轉折點，模型截面撓度呈下降趨勢，其下降較緩。當斜腿傾斜角度減小至40°后，撓度曲線再一次出現轉折點，且模型截面撓度呈上升趨勢，上升較陡。

圖12 斜腿傾斜角度對撓度的影響

圖12中跨中截面及斜腿頂截面的撓度變化規律皆是隨著斜腿角度的減小，呈先增后減再增趨勢。因此，在斜腿剛構橋結構設計時其斜腿傾斜角度為45°～55°時較為合理。

5 結論

通過模型試驗及有限元分析可得出以下結論:

1)試驗所揭示的受力特性的變化規律與理論計算、有限元分析結果一致。

2)模型截面應力及撓度的實測值與有限元分析值基本吻合，跨中截面拉應力平均偏差值為11.17%，斜腿頂截面拉應力平均偏差值為8.08%，斜腿底截面拉應力平均偏差值為11.49%，跨中撓度平均偏差值為9.92%，驗證了有限元分析的可行性。

3)有限元模擬出分跨比在0.65～0.75之間、斜腿角度在45°～55°之間時，斜腿剛構橋模型的跨中撓度較小，受力較合理。

4)板式截面的斜腿剛構橋整體受力性能較好，適用于中等跨徑橋梁結構。

［1］朱曉寧，葛云，責慶國.整體式橋臺橋梁的發展及應用［J］.現代交通技術，2006(6):30－33.

［2］王昌武，丁銳，王國鼎.無橋臺斜腿剛架橋結構特性分析［J］.中南公路工程，1998，23(1):47 －49.

［3］王昌武.無橋臺斜腿剛架橋力學特性分析［J］.武漢城市建設學院報，1998(3):37－40.

［4］楊軍猛，郭俊峰.斜腿剛構橋受力特性研究［J］.交通科技，2011(1):13－15.

［5］劉世忠.大跨度預應力斜腿剛構橋的整體模型試驗［J］.蘭州鐵道學院學報，1995，14(4):21 －26.

［6］仇祚禮.預應力斜腿剛構橋實體有限元分析［J］.價值工程，2005(7):60－62.