廣義數域篩法對公鑰加密算法的攻擊

侯方天，張雅琨

(中國傳媒大學信息工程學院，北京市100024)

1 引言

RSA是一種非常流行的公鑰加密算法，如今被應用在許多的電子商業(yè)系統(tǒng)中，如網站的瀏覽器和服務器系統(tǒng)、電子郵件系統(tǒng)、遠程會議安全和電子信用卡支付系統(tǒng)等，它是建立在大整數很難因式分解的基礎之上的，所以對大整數做因數分解的難度決定了RSA算法的可靠性，隨著整數分解算法的不斷改進和計算機運算速度的加快，人們對RSA系統(tǒng)的安全性又產生了懷疑。本文將介紹大整數分解的一種重要的算法——廣義數域篩法(GNFS)。

廣義數域篩法(GNFS)是數域篩法(NFS)的一般形式，比較適于分解130位以上的大整數。NFS其還有一種特殊的形式，被稱為特殊數域篩法(SNFS)，SNFS分解的大整數w要滿足形式w=re±s，其中 r，e，s∈Z，并且 e＞0，在 07 年的春天就有科學家通過SNFS分解了1039bit的大整數，但由于SNFS對所要分解的大整數有著特殊的形式要求，它比用GNFS分解768bit的大整數在難度上要小得多。

廣義數域篩法(GNFS)是一種很好的因式分解的方法，到目前為止，有效的因式分解方法還有很多，譬如試除法，Pollard’s rho分解法，Pollard’s P-1分解法，橢圓曲線分解法，基于完全平方的分解算法［1］，各算法的特點如表1所示。

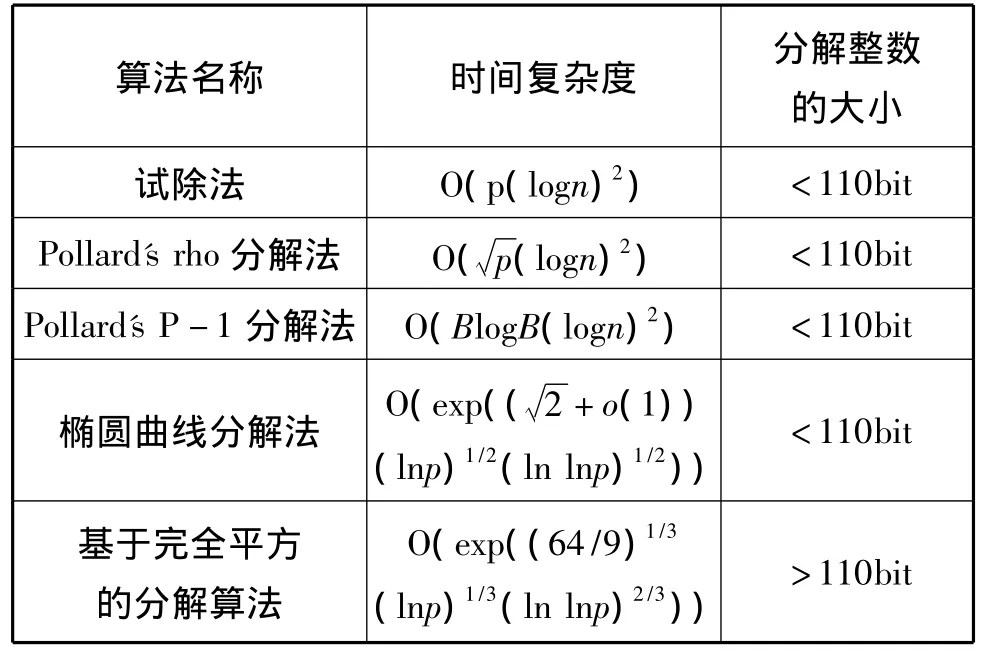
表1 因式分解各算法特點

GNFS是一種很好的基于完全平方的分解算法，它對分解大整數的效率相對較高，本文將結合RSA-768的破解過程［2］，對GNFS的相關理論和操作步驟做出相應說明。

2 二次篩法(QS)

二次篩法與數域篩法有著相似的理論基礎，為了更好的理解數域篩法，我們首先來研究一下二次篩法。

從費馬、歐拉、高斯開始，一直到現在，一般整數分解方法基本上都是在“同余式的平方組合”上做文章，同時也會再加上一些現代技巧，如因數基、平滑數、篩法、線性代數等［3］。現在假定想分解的數n，如果能夠找到兩個正整數 x和 y，滿足 x2=y2(mod n)并且0＜x＜y＜n，x≠y，x+y≠n則 gcd(x+y，n)和gcd(x-y，n)有可能就是n分解的兩個因數。

QS是一種很好的因式分解的方法，一般適合分解130位以下的整數，它的核心是Dixon的隨機二次理論，該理論的核心是要通過運用因數基、平滑和二次剩余類中向量的相關性等概念計算出相應的平方值。在QS中，因數基為非空的素數集合，假設為F，如果一個整數k的所有分解的素數都在集合F中，那就稱該整數k在因數基F上平滑。

現在固定一個因數基 F={p1，p2，…，pm}，選取一個等式f(x)=x2(mod n)，計算出合適的值ri，使得f(ri)在因數基F上平滑，當有m個ri被找到后，

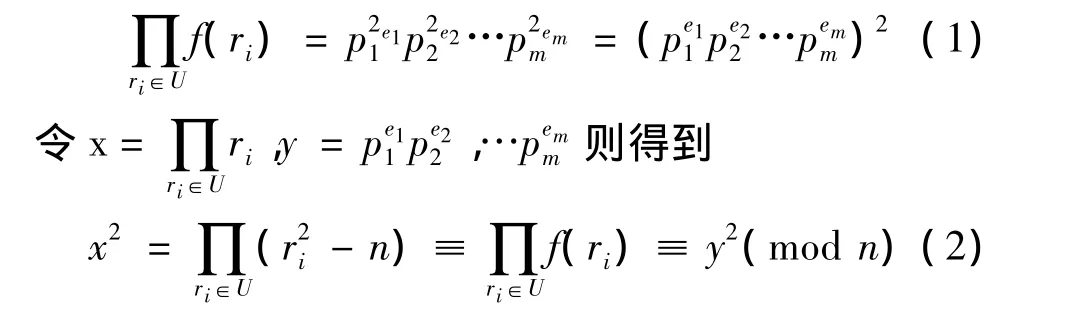
這就得到了我們所需要的配對(x，y)。

舉個簡單的例子，先假設因數基F為(-1，2，3，5，7)，f(ri)為一些隨機整數的平方，但要保證 f(ri)在因數基F上平滑，取n=33，隨機取f(ri)的值結果如表2所示。

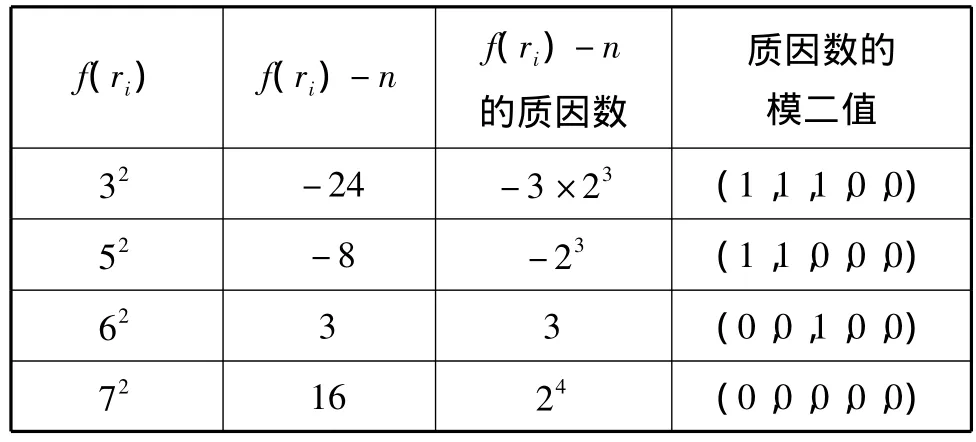
表2 f(ri)的取值結果

從線性代數的角度上來看，只要能在質因數模二值構成的向量中找到一個線性相關組，就能找到所需要的配對組合(x，y)。從表中可以看到，當f(ri)=72時，向量跟自身線性相關，于是可以得到72≡222≡42(mod 33)，從而可以計算出 gcd(7±4，33)=(3，11)，當向量跟自身不相關時，可以通過和別的向量組合，一起組成一個線性相關組，當把f(ri)等于52和62的質因數的模二值相加后，向量為(1，1，1，0，0)，正好與 f(ri)等于 32的向量線性相關，于是可以得到32≡(5×6)2(mod 33)，gcd(30 ±3，33)=(3，11)。

從以上的分析可以看出，二次篩法最主要的步驟就是通過篩選獲取在因數基上平滑的數，然后通過計算找到線性相關的向量組，最后以一定概率分解大整數，廣義數域篩法的主要步驟也大體如此。當然廣義數域篩法也有著其自身的特點，對于那些大于130位的整數，廣義數域篩法有著更高的分解效率，篩法中所選取的不可約多項式f(ri)的最高次數不再僅僅是二次，高次的多項式可以產生更多在因數基上平滑的數。在二次篩法中，f(ri)起到了一個橋梁的作用，他把整數Z映射到了n次剩余類，Z/n Z把一個在Z中的完全平方數映射到了一個在Z/n Z中的完全平方數，這種映射的方法在廣義數域篩中也有著重要的作用，兩者的不同點在于QS操作的數都是整數，映射是從Z到Z/n Z，而廣義數域篩操作的數除了整數，還有環(huán)Z［α］，映射包括了兩部分，一部分是從Z到Z/n Z，還有一部分是從Z［α］到Z/n Z，這部分映射用φ(β)來表示，這就使廣義數域篩法相比二次篩法顯得更加得復雜。

3 廣義的數域篩法(GNFS)

廣義的數域篩法的分解理論和技術包括多項式選擇、篩選、矩陣形成和線性相關以及平方根的求解，同二次篩法一樣，廣義的數域篩法也是基于“同余式的平方組合”，目的是找到更多的配對組合(x，y)，從而分解大整數，正如上文提到的，廣義的數域篩法的操作的數還包括環(huán)Z［α］，其中α是多項式f(x)的根，根的集合形成了集合ψ，在這個環(huán)Z［α］上能產生更多的平滑，于是廣義的數域篩法產生配對組合(x，y)的兩個基礎方程分別為:

其中 α∈ψ，z∈Z，β =f'(θ)·α∈Z［θ］y=f'(m)·z，x=φ(β)∈Z/n Z。

通過恒等式(5)可以看到，廣義的數域篩法要想找到合適的配對組合(x，y)，就得找到足夠的配對組合(a，b)，使得a+bθ在代數因數基Z上平滑，a+bm在有理數因數基Z上平滑，然后計算出(x，y)，以50%左右的可能性得到整數n的分解因式。

廣義的數域篩法的分解步驟如下所示。

3.1 多項式選擇

多項式的選擇是廣義數域篩法的第一步，它對整個篩法的耗時量和篩選的復雜程度有著重要的作用。

廣義數域篩法一般會選取一個不可約的d階多項式 f(x)，α為這多項式的一個復根，Z［α］?Z［x］/f(x)，然后選取一個參數m∈Z/n Z，通過 Murphy的多項式選取法，使得f(m)≡0(mod N)，N為所要分解的大整數，令m為N的一個分解基，則N，其中 ci∈Z 并且 0≤ci≤m-1，當時，很容易得到，f(m)=N≡0(mod N)滿足等式的要求。由映射φ:Z［α］→Z/n Z，得到φ(α)=m，這樣就使Z［α］的值同整數有了對應關系。

在實踐中，需要通過大量的實驗，參數的細致調整，憑借經驗，有時再加上點運氣，才能尋找到一個最合適的多項式。一般來說，首先會確定多項式的次數d，d的大小由所要分解的大整數N的位數有關［4］，當分解50～80位的十進制整數時，會取d值為3;80～110位的十進制整數時，取d值為4;120～220為十進制整數時，取d值為5;當分解220～300位十進制整數時，取d值為6。然后確定參數m的值，通常取m值為或其附近的某一整數，多項式的選擇有很多不確定因素，多項式的次數d的選取，參數m的取值都有很強的隨機性，即使確定了一組d和m，多項式的系數還可以有不同的選擇，只有通過實驗，根據得到的合適的整數對(a，b)的數量才能確定多項式的好壞。

RSA-768的團隊通過三個月的時間，從260個多項式中選出了3個符合要求的質量很高的多項式，而他們最終決定采用的多項式為

RSA-768的團隊同時也選取了一個一階的多項式用來在整數環(huán)上進行計算，多項式為

3.2 平滑和因數基

從二次篩法中可以看出，平滑和因數基是篩法的基礎，通過找到足夠多的在因數基上平滑的數，才能順利分解大整數，廣義的數域篩法也是這樣，不過因為其不光在整數域上操作，還要在環(huán)Z［α］上操作，所以在環(huán)Z［α］對于平滑和因數基就有了新的定義，因數基不再是Z［α］中的素數，而是其理想。

α是多項式的根，定義 N(α)=σ1(α)σ2(α)σ3(α)…σd(α)，其中 σi是從 Q［θ］到 C 的映射，D 為一綽金環(huán)，P為D的一個素理想，p代表一些素數，當N(P)=p時，定義P為D的第一階素理想，當r屬于 Z/p Z，并且 f(r)≡0(mod p)時，集合(r，p)同第一階素理想的集合一一映射，理想p決定了組合(r，p)，廣義數域篩法要找的因數基就是集合(r，p)。

廣義數域篩法中定義了三個因數基，為有理數因數基、代數因數基和二次特征基。

有理數因數基跟二次篩法中的因數基一樣，都是在整數域上操作，通過對(a，b)的取值，找到在a+bm上平滑的值，為了和代數因數基和二次特征基的形式保持一致，在實踐中一般選取因數基的形式為(m(mod p)，p)。

上文提到過不可約多項式f(x)根形成的集合為O，由數論的相關知識可知，環(huán)O是一個綽金環(huán)，它的一些理想可以被分解為素理想，從O的理想中選取一個集合I，這個集合I就被稱為代數因數基，然后找一對組合(a，b)，使得a+bθ有一個主理想，能完全分解成I上的素理想，這樣的元素a+bθ就被稱為在I上平滑。

二次特征基是用來確定a+bθ在Z［θ］上是否為一個完全平方數，廣義數域篩法的一個基礎方程為

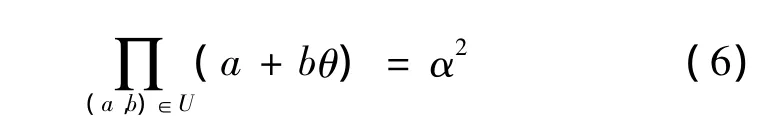
給定一個第一階素理想Q，它決定了組合(s，q)，當Q不能分解主理想〈a+bθ〉，并且f'(s)≠0(mod q)時，也就是說，如果a+bθ在Z［θ］上是一個完全平方數，那么當然這是一個必要條件，不是說當等式成立時，a+bθ就一定是完全平方數，通常在實際計算的時候，q會取比p大一點的值。

3.3 篩選

篩選是廣義數域篩法中最重要也是最耗時的步驟之一，可以通過并行處理的方式提高效率，篩選的目的是要得到足夠多的整數對(a，b)，使得a+bm在有理數因數基Z上平滑，a+bθ在代數因數基Z［θ］上平滑，而對兩者篩選的方法大體一致。

對于a+bm來說，m已經在上文確定，還有兩個變量a和b，當固定b的值(通常先取b=1)，再取-u＜a＜u(u是a的取值的范圍，可視情況而定)，a從-u開始一直取到u，通過計算得到能使a+bm在因數基上平滑的組合(a，b)，當取完a的值發(fā)現組合還不夠時，增加b的值直到組合夠為止，這種方法需要計算每個a+bm的值是否平滑，很消耗時間。在實際中一般會固定一個因數基里的素數p和一個正整數b，當a+bm≡0(mod p)，也就是a≡-bm(mod p)的時候，p就能分解，a+bm那么在篩選的時候，在-u到u的范圍內取滿足等式a=-bm+kp的a的值就可以了，這就大大提高了效率。

a+bθ的篩選是在代數因數基上進行的，是要通過第一階素理想P來分解主理想〈a+bθ〉，而P可以由組合(r，p)決定，當a≡-br(mod p)的時候，p能分解，N(a+bθ)而當 p能分解 N(a+bθ)的時候，第一階素理想P也就能分解主理想〈a+bθ〉，于是篩選的方法就是固定b的值和組合(r，p)，取a≡-br+kp，并且 -u ＜a＜ u，然后計算 N(a+bθ)的值，當值能被p分解時，(a，b)就是篩選出來的可用的整數對。

通過篩選，RSA-768的團隊總共獲取了64334489730對合適的組合，然后通過分布式篩選理論，其中有24.7%的組合是重復記錄的，然后通過一種判別算法，刪去那些包含素數(小概率出現)的組合，于是就只剩下2458248361對組合，只占原來的3.4%。

3.4 矩陣生成及過濾

通過篩選，得到了I對整數對(a，b)，接下來就要構建一個矩陣，假設有理數因數基有k個素數，代數因數基有l(wèi)個第一階素理想，二次特征基有m個第一階素理想，則矩陣應該有k+l+m+1行，列數為I，矩陣的每一列都由一對整數對(a，b)決定，構建矩陣的最終目的是尋找到矩陣列與列之間的線性相關性，從而找到不同的 a+bm，〈a+bθ〉和 a+bθ，使他們的乘積值為完全平方數。

每一列矩陣都是由四部分組成，第一部分就一位，它表示a+bm的正負性，正的話為0，負的話為1;第二部分有k位，有理數因數基中的素數有k個，a+bm由這些素數分解后素數的指數模二的值就對應了該k位，假設因數基為{2，3，5}，選定的整數對為(3，1)，m 為27，則 a+bm=30=2 ×3×5，前 k位就為(1，1，1);第三部分有l(wèi)位，代數因數基中有一對(r，p)，通過公式 N(a+bθ)=(-b)df(-a/b)計算出 N(a+bθ)的值，把 N(a+bθ)分解得到 p，當 a≡-br(mod p)時，記該位為1;第四部分有m位，由二次特征基決定，當滿足公式時，值為0，否則為1.

以上生成的是一個原始矩陣，矩陣維數和重量會直接決定線性相關求解的時間，原始矩陣顯然不是最合適的矩陣，必須通過相應的過濾方法，減小矩陣的維數，同時控制重量的增長，使兩者達到一個最佳平衡點，這樣能大大提高分解效率。

3.5 線性相關

當最佳矩陣找到后，就得通過計算得到矩陣列向量之間的線性相關性了，這也可以理解為求解一個大規(guī)模稀疏線性方程組，用傳統(tǒng)的高斯消元法去處理一個維數很大的矩陣時會消耗很多時間，不能被采用，目前最常用的求解的方法為 Lanczos和Wiedemann算法［5］，尋找線性相關性的這一步是數域篩法中耗時最多的步驟之一，實際中通常會采用并行處理。

RSA-768的團隊最后生成了一個192796550*192795550的矩陣，矩陣的重量為27797115920，也就是說每行平均有144個非0數，通過119天的計算，團隊最終在2009年的十月八號完成了矩陣的計算，得到了能使矩陣列向量線性相關的組合。

3.6 平方根的求解

用廣義數域篩法分解大整數，利用的是“同余式的平方組合”，這就需要利用LLL算法或是Montgomery的算法［6］，來求解整數的平方根，同過大規(guī)模稀疏線性方程組的求解，就能找到對應的平方關系，這些平方關系都是由幾對組合(a，b)確定的，通過組合(a，b)得到，而β2=f'(θ)2·α2，從而計算出 β 的含 θ的多項式 f2(θ)，于是 x=f2(m)≡φ(β)(mod N);通過組合(a，b)得，而 y2=f'(m)2·Z2，通過平方根的求解就能得到y(tǒng)的值。

4 結論

本文討論了數域篩法中廣義數域篩法的基本理論，從中可以看出，廣義數域篩法的分解步驟是相對固定的，首先要選擇一個合適的多項式，多項式質量的好壞決定了篩選的效率，然后要確定三個因數基，以平滑為標準進行篩選，篩選可以采取并行處理［7］，當篩選出有效的組合后，就可以組成一個矩陣，并對其進行處理，找到線性相關的列向量，這一步驟計算量很大，需進行并行處理，通過平方根的求解，得到組合(x，y)，最終以50%左右的可能性完成對大整數的分解。

對于廣義數域篩法來說，雖然還存有很多問題需要解決，但作為目前對大整數分解最快的方法，通過硬件設備和算法的改良，其每一分解步驟都有改進的空間，從而能夠更加高效的完成大整數的分解，從而完成對公鑰加密算法RSA的攻擊。

［1］ T Kleinjung，K Aoki，J Franke，A Lenstra.Factorization of a 768-bit rsa modulus［J］.Cryptology ePrint Archive，Report.2010/006，2010.

［2］ M E Briggs.An introduction to the general number field sieve［D］.Virginia Polytechnic Institute and State University，USA，1998.

［3］ J Hill.The Number Field Sieve:An Extended Abstract［D］.March 12，2010.

［4］ 王洪濤，劉春雷.數域篩法中多項式的選擇［J］.信息工程大學學報，2003，4(3).

［5］ L T Yang，Li X，J H Park.A Parallel GNFS Algorithm with the Improved Linbox Montgomery Block Lanczos Method for Integer Factorization［J］.International Conference on Information Se-curityandAssurance，2008.

［6］ AKLenstra，HWLenstra，MSManasse.The numberfieldsieve［D］.

［7］ 顏松遠.整數分解［M］.北京:科學出版社，2009.