單載波系統均衡技術的研究

林霖

(中國傳媒大學廣播電視數字化教育部工程研究中心，北京100024)

1 引言

均衡是通過信號接收端產生與信道相反的特性，用來抵消信道的時變多徑傳播特性引起的碼間干擾，消除信道的頻率和時間選擇性的一種技術。1965年Lucky設計了第一個自適應均衡器——“迫零自適應均衡器”，此后在對均衡的研究中，人們分別提出了卡爾曼算法和LMS算法，近年來的研究多圍繞均衡器的改進算法及其在通信中的應用。

目前的信道均衡方法主要有:無數據輔助的盲均衡方法、基于訓練序列的均衡方法、半盲均衡方法。按時頻域進行均衡的不同，又可以分為時域均衡和頻域均衡。

下面將先對單載波均衡技術進行介紹，然后對單載波幀結構的設計及HDFE結構的均衡算法進行分析。

2 單載波頻域均衡

多徑干擾是中短波廣播中很常見和必須解決的一個問題。早在模擬信號處理階段，均衡被作為對抗ISI的主要方法而提出。與時域上進行濾波處理相對應的，也可以在頻域上對信號分別進行補償信號幅度和相位，即頻域均衡。

頻域均衡的基本思想是，利用可調濾波器的頻率特性去補償基帶系統的頻率特性，使包括可調濾波器在內的基帶系統的總特性滿足無失真傳輸的要求。相對于時域中需要較長抽頭的濾波器來說，可以大大節省所需乘法的數目。框圖如圖1所示。

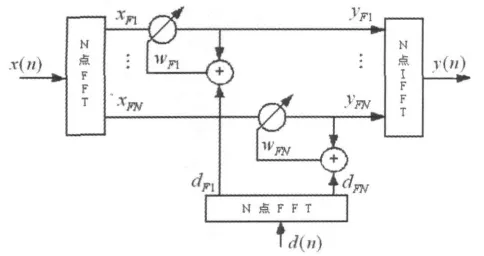
圖1 頻域均衡框圖

2.1 單載波幀結構的設計

在OFDM系統中常通過插入長度大于信道的最大傳輸時延時循環前綴(Circle Prefix，CP)來消除碼間干擾(ISI)。與此類似地，單載波幀序列也可以通過加獨特碼(Unique Word，UW)消除 ISI，而且不像CP只能用作保護間隔，而UW能用作信道估計、均衡和同步。加UW的幀結構如圖2:

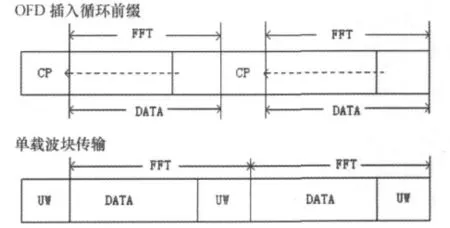
圖2 加UW的幀結構

基于獨特碼(UW)的單載波頻域均衡(SC—FDE)傳輸系統以負載幀格式進行傳輸，每一段負載數據與后面的UW序列組成一個數據塊，UW序列的插入使得數據塊具有理想的周期性的自相關特性。進行負載幀格式傳輸的單載波傳輸框圖如圖3所示。

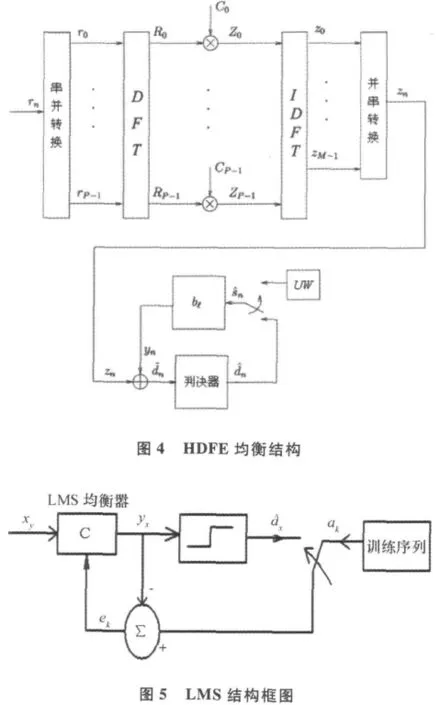
2.2 改進后的混合判決反饋均衡HDFE的設計

單純的時域均衡需要較長抽頭的濾波器，單純的頻域均衡因進行需要對一段時間內數據塊一起進行DFT，具有非實時性，所以將傳統的純時域或純頻域的均衡結合起來會有較好效果。

前饋濾波可采用ZF破零或MMSE均衡算法，后饋濾波可采用維納、或LMS、RLS等自適應均衡法，下面將重點介紹后饋濾波中LMS算法。

3 后饋濾波中的LMS算法

3.1 LMS原理

LMS遵循的是最小均方誤差準則，使最小均方誤差最小即使代價函數J最小

J=E［e2(n)］=E［d2(n)-2d(n)y(n)+y2(n)］

LMS采用最陡下降法對其系數C進行調節，最

圖3 加UW的單載波傳輸框圖

改進后的結構是時域頻域混合的，前饋濾波器對M個樣值得數據塊FFT變換，進行頻域域均衡，反饋濾波器則是逐個符號進行時域均衡。

前饋濾波器采用頻域均衡，可采用相對時域均衡少得均衡抽頭系數，簡化了運算，后饋濾波器采用時域均衡彌補了前饋DFT非實時性均衡的缺點。

終使J最小化，達到最佳濾波狀態。運用最陡下降法，即下一個權矢量等于現在的權矢量加一個正比于梯度的變化量。得到系數

C(n+1)=C(n)+2μeμX(n)

其中μ是一個正常數，通常稱它為自適應收斂系數或步長。步長增大，收斂越快，均衡的跟蹤越快。但是步長越大，均方誤差也就越大。所以步長的選擇應該在跟蹤速度和減小均方誤差之間折衷。

3.2 LMS工作流程

LMS自適應均衡器可以有兩種模式:訓練模式和面向判決模式

訓練模式:發送一串已知的訓練序列，然后進行訓練模式下的LMS自適應均衡，步驟如下

在HDFE結構中可以將UW作為已知訓練序列。

面向判決模式:當訓練序列均衡結束后，LMS自適應均衡器轉向面向判決模式，進行新的LMS自適應均衡，步驟如下

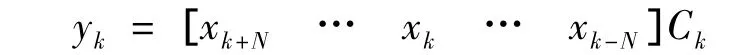
對yk進行判決，得到ak的判決值ak

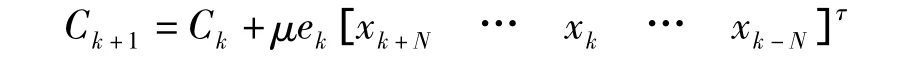
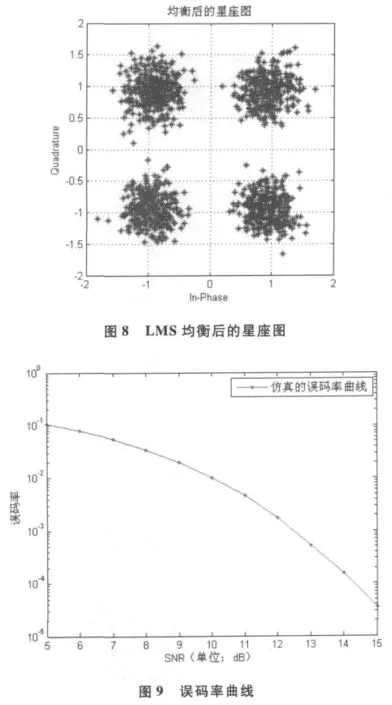
3.3 仿真結果及分析

以下是對QAM調制數據進行LMS均衡后的星座圖及誤比特圖，其中步長取0.05。

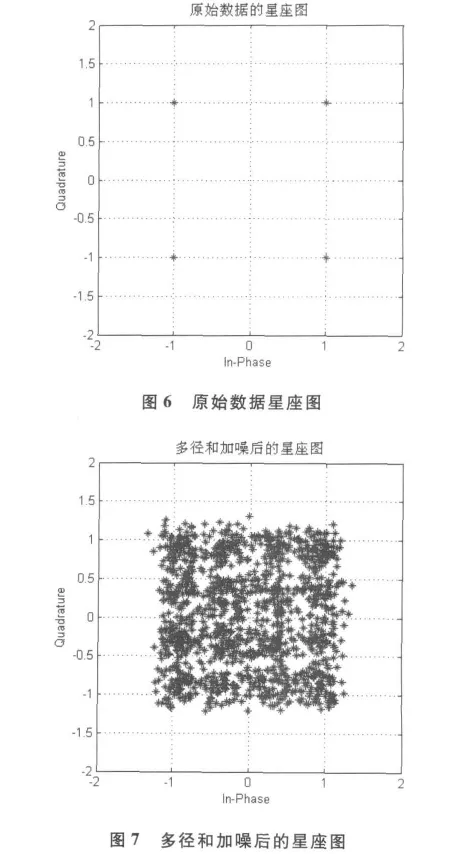
經過均衡后星座圖清晰，有較低的誤比特率。均衡效果較好。

4 結束語

本文簡單了介紹了單載波均衡的原理，及改進后的均衡結構。重點分析了時頻混合域判決反饋式均衡(HDFE)結構和算法，并對LMS均衡方法仿真，具有良好性能。

［1］車晴.電子系統仿真與MATLAB［M］.北京:北京廣播學院出版社，2000.

［2］李強，雷霞，羅顯平.無線通信中迭代均衡技術［M］.北京:國防工業出版社，2011.

［3］John G.Proakis，著;張力軍，等，譯. 數字通信(2版)［M］.北京:電子工業出版社，2003.

［4］周炯槃，龐沁華，等.通信原理合訂本［M］.北京:北京郵電大學出版社，2005.

［5］樊昌信，曹麗娜.通信原理(第6版)［M］.北京:國防工業出版社，2007.

［6］程佩青，數字信號處理教程(第3版)［M］.北京:清華大學出版社，2007.

［7］Nevio Benvenuto，Rui Dinis.Single Carrier Modulation With Nonlinear Frequency Domain Equalization:An Idea Whose Time Has Come Again［J］.IEEE，Proceedings of the IEEE，2010，98(1).