具有抑制作用和離散時滯的捕食系統的Hopf分岔分析

王新慧，劉海鴻

(云南師范大學數學學院，云南昆明650092)

具有抑制作用和離散時滯的捕食系統的Hopf分岔分析

王新慧，劉海鴻

(云南師范大學數學學院，云南昆明650092)

研究了一類具有抑制作用和離散時滯的捕食－食餌模型，通過分析該模型在正平衡點的線性化方程及其相應的特征方程，研究了正平衡點漸近穩定性并證明了Hopf分岔的存在.通過應用規范型理論和中心流形定理，得到了確定Hopf分岔方向和分岔周期解的穩定性計算公式.最后，利用數值模擬驗證了研究結果.

Lotka－Volterra捕食－食餌系統;離散時滯;穩定性;Hopf分岔;周期解;抑制作用

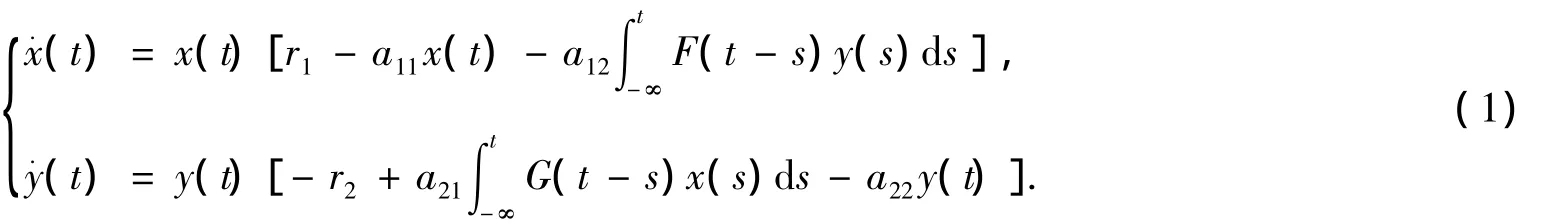
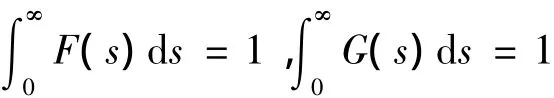
當F(s)，G(s)取不同形式時，很多學者已經做了廣泛的研究［3－11］，例如，F(s)=G(s)=δ(s)時(δ為Dirac delta函數)，Chen［3］，Zhang［11］等研究指出系統(1)正平衡點的存在性暗示了它的全局穩定性.1973年May［12］首次提出并討論了當系統(1)F(s)=δ(s－τ)，G(s)=δ(s)時的帶有單個離散時滯的捕食－食餌模型:

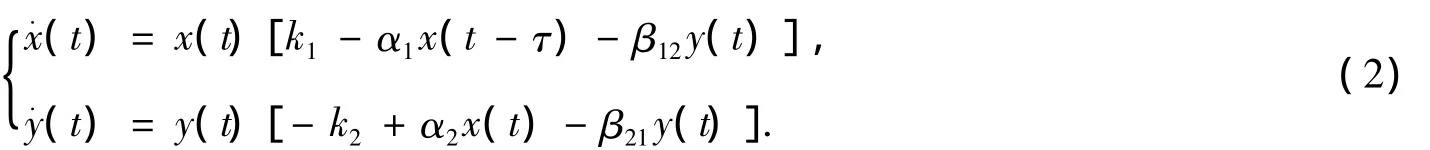
Song和Wei［6］研究了系統(2)把τ作為分岔參數時τ對動力系統(2)的影響.F(s)=δ(s－τ)，(τ≥0)，G(s)=δ(s－η)(η≥0)時，(1)轉化為如下形式:

Faria［4］，Ruan［5］，Yan和Chu［8］，He［13］，Lu和Wang［14］分別對(3)做了不同的研究.

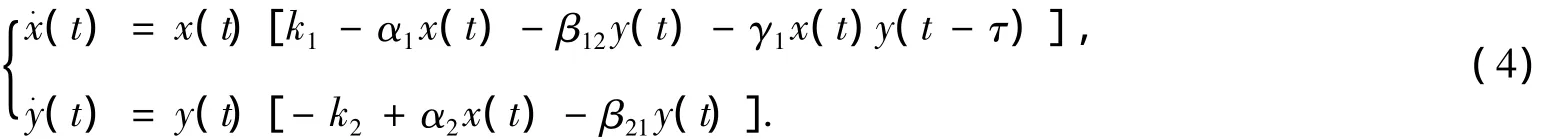
其中，x(t)，y(t)分別表示食餌、捕食者種群的密度;k1＞0，k2＞0為食餌的增長率和捕食動物的死亡率，參數α1，α2，β12，β21，γ1均為正常數.本文研究了時滯τ對系統(4)的影響.通過研究發現時滯能導致捕食－食餌系統產生震蕩.所以，由產生毒素而出現的捕食時滯會影響不同捕食模型的種群密度，從而影響季節繁殖、生長.因此對此問題的研究具有重要的意義.經過查閱大量文獻還沒發現從此角度考慮的研究.

1 正平衡點的穩定性和Hopf分岔的存在性

通過計算，當條件H1):k1α2＞k2α1成立時，式(4)存在唯一正平衡點E(x*，y*)，其中，

模袋混凝土的充灌是整個施工過程中的關鍵工序，要做到混凝土攪拌、運送、泵送、充灌成形一條龍作業，把握好充灌速度。所需混凝土必須嚴格按配合比攪拌，保證坍落度、強度等指標。充灌混凝土的順序采取自下而上逐排口逐倉充灌 (每4 m為1個灌口)，每排的充灌順序為：由模袋搭接的一側開始向另一側逐口充灌，采用這樣的充灌順序實際上是幾條模袋輪流交替充灌。與同一次連續充滿一條模袋后再充灌下一條模袋的順序相比，這樣的順序有以下優點：

其中，M=－α1x*－γ1x*y*，N=－β12x*，Q=－γ1(x*)2，a11=－(α1+γ1y*)，a12=－β12，，a13=－2γ1x*，a14=－γ1，D=α2y*，E=－β21y*，b11=－β21，b12=α2.顯然，通過變量變換，(4)的正平衡點E(x*，y*)轉化為(5)的平衡點E*(0，0).易計算系統(5)在平衡點E*(0，0)性化系統的特征方程為:

其中，a1=－(M+E)，a0=ME－DN，b0=－DQ.

1)當τ=0時，(6)轉化為λ2+a1λ+a0+b0=0.通過計算，易得a1＞0，a1(a0+b0)＞0，由Routh－Hurwitz定理可知式(6)的2個根均具有負實部，因此當τ=0時，正平衡點是局部漸近穩定的.

2)當τ≠0時，設λ=iω(ω＞0)是式(6)的根，則－ω2+ia1ω+a0+b0(cos(ωτ)－i sin(ωτ))= 0.分離實部和虛部得－ω2+a0+b0cos(ωτ)=0，a1ω－b0sin(ωτ)=0，把上式兩端平方相加得

定理1如果系統(4)中系數ki，αi(i=1，2)滿足條件H1)，ai(i=0，1)，b0滿足H2)，則當τ∈［0，τ0)時，式(4)的正平衡點是漸近穩定點;當τ＞τ0時，式(4)的正平衡點是不穩定點;當τ=τj(j=0，1，2，…)時，式(4)在正平衡點附近出現Hopf分岔.

2 Hopf分岔的性質

運用Hassard在文獻［19］中介紹的方法，討論式(4)正平衡點附近分岔周期解的穩定性及Hopf分岔方向.在系統(5)中，令x－k(t)=xk(τt)，為了書寫簡便，記x－k(t)為xk(t)，則系統(5)轉化為如下模型

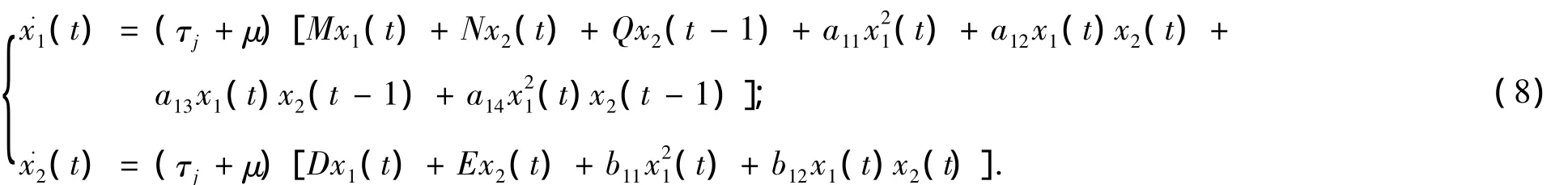
定義線性算子L(μ):→R2和非線性算子f(·，μ):C→R2

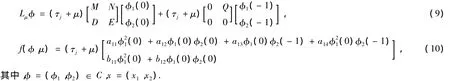
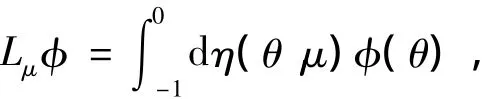
其中δ表示狄拉克函數對于φ∈C1(［－1，0］，R2)，定義

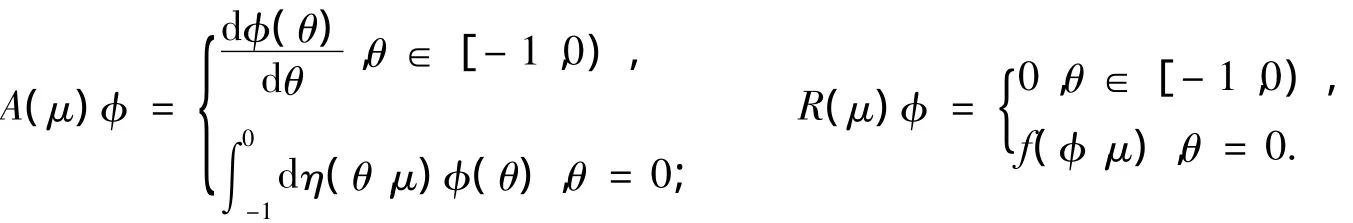
則(8)等價于x.t=A(μ)xt+R(μ)xt.對于ψ∈C1(［0，1］，(R2)*)定義

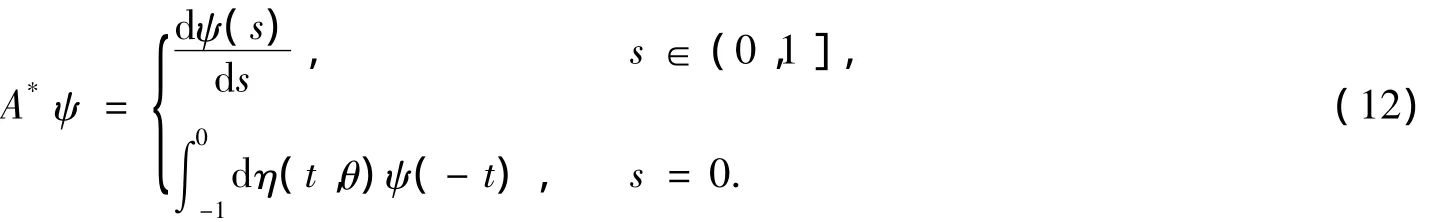
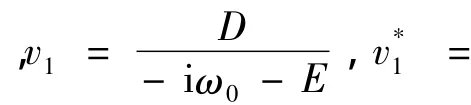
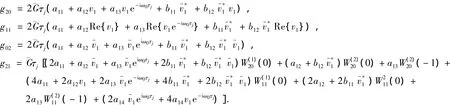
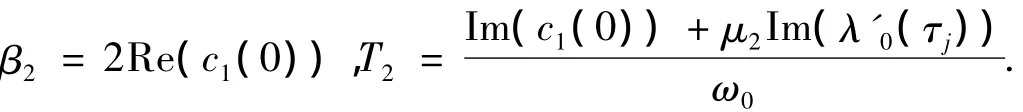
詳細計算過程參看文獻［19］.通過上面的討論，可以得到下面結果.

定理1μ2決定了Hopf分岔的方向;如果μ2＞0(＜0)，則Hopf分岔是超臨界(亞臨界)的;β2決定了分岔的穩定性;如果β2＞0(＜0)，分岔周期解是不穩定(穩定)的;T2決定了分岔周期解的周期;如果T2＞0(＜0)，周期是增加(減少)的.

3 數值模擬及分析

利用數學計算軟件Matlab和Xppant對前面的討論結果進行數值模擬.考慮系統，

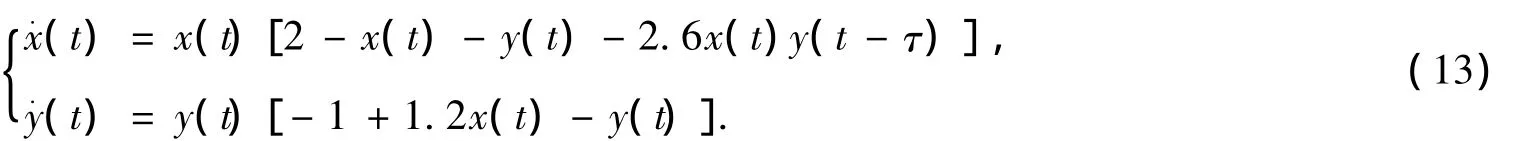
經計算E(1.046 8，0.2561 8)，ω0=0.263 88，τ0=9.455 78.由定理1可知:當τ＜τ0時，正平衡點E(1.046 8，0.256 1)是局部漸近穩定點，數值仿真如圖1所示;當τ比τ0稍大時，系統(4)在正平衡點E附近產生Hopf分岔周期解，對應的數值仿真如圖1所示.

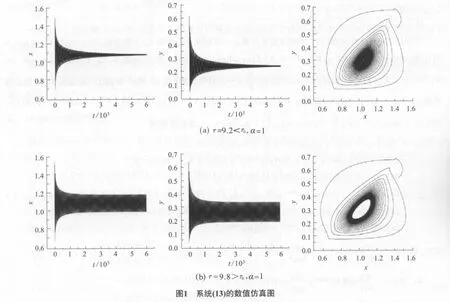
由圖1(a)可見當τ=9.2＜τ0，α=1時，系統(13)的數值仿真圖正平衡點E(1.046 8，0.256 1)是漸近穩定的.由圖1(b)可見當τ=9.8＞τ0，α=1時，系統(13)的數值仿真圖正平衡點E(1.046 8，0.256 1)不穩定并且一個穩定的周期解從E(1.046 8，0.256 1)處分岔出來.

4 結語

論文討論了式(4)正平衡點的穩定性以及Hopf分岔的存在性，并應用中心流形定理和規范型理論討論正平衡點分岔的方向以及分岔周期解的穩定性，最后，通過數值模擬對相應理論結果加以驗證.

［1］VOLTERRA V.Lecons sur la th'eorie math'ematique de la lutte pour la vie［M］.Paris:Gauthier－viuars，1931.

［2］BRELOT M.Sur le probl`eme biologique h'er'editaire de deux esp`eces d'evorante et d'evor'e［J］.Ann Mate Pura Appl，1931，9:58－74.

［3］CHEN L.Mathematical models and methods in ecology［M］.Beijing:Science Press，1988.

［4］FARIA T.Stability and bifurcation for a delayed predator－prey model and the effect of diffusion［J］.J Math Anal Appl，2001，254(2):433－463.

［5］RUAN S.Absolute stability，conditional stability and bifurcation in Kolmogorov－type predator－prey systemwith discrete delays［J］.Quart Appl Math，2001，59(1):159－172.

［6］SONG Y，WEI J.Local Hopf bifurcation and global periodic solutions in a delayed predator－prey system［J］.J Math Anal Appl，2005，301(1):1－21.

［7］SONG Y，YUAN S.Bifurcation analysis in a predator－prey system with time delay［J］.Nonlinear Anal:Real World Appl，2006，7(2):265－284.

［8］YAN X P，CHU Y D.Stability and bifurcation analysis for a delayed Lotka－Volterra predator－prey system［J］.Comput Appl Math，2006，196(1):198－210.

［9］YAN X P，LI W T.Hopf bifurcation and global periodic solutions in a delayed predator－prey system［J］.Appl Math Comput，2006，177(1):427－445.

［10］YAN X P，ZHANG C H.Hopf bifurcation in a delayed Lokta－Volterra predator－prey system［J］.Nonlinear Anal，RWA 2008，9(1):114－127.

［11］ZHANG J，FENG B.Geometric theory and bifurcation problems of ordinary differential equations［M］.Beijing:Beijing University Press，2000.

［12］MAY R M.Time delay versus stability in population models with two and three trophic levels［J］.Ecology，1973，54(2):315–325.

［13］HE X Z.Stability and delays in a predator－prey system［J］.J Math Anal Appl，1996，198(2):355－370.

［14］LU Z，WANG W.Global stability for two－species Lotka－Volterra systems with delay［J］.J Math Anal Appl，1997，208(1): 277－280.

［15］RICE E L.Allelopathy［M］.New York:Academic Press，1984.

［16］MAYNARD SMITH J.Models in ecology［M］.Cambridge:Cambridge University，1974.

［17］CHATTOPADHYAY J.Effects of toxic substance on a two－species competitive system［J］.Ecol Modl，1996，84(1/2/3):287－289.

［18］MUKHOPADHYAY A，CHATTOPADHYAY J，TAPASWI P K.A delay differential equation model of plankton allelopathy［J］.Mathematical Biosciences，1998，149(2):167－189.

［19］HASSARD B D，KAZARINOFF N D，WAN Y H.Theory and applications of Hopf bifurcation［M］.Cambridge:Cambridge Univ Press，1981.

［20］徐雪嬌，林怡平.一類具有時滯的Lotka－volterra系統的Hopf分支與混沌控制［J］.云南師范大學學報:自然科學版，2010，30(4):28－33.

［21］張俊麗，陳斯養.一類具有時滯的廣義造血模型的Hopf分支［J］.云南師范大學學報:自然科學版，2010，30(6):34－38.

(責任編輯梁志茂)

Analysis of Hopf Bifurcation in a Predator－Prey System of Population Allelopathy with a Discrete Delay

WANG Xin-hui，LIU Hai-hong
(Department of Mathematics，Yunnan Normal University，Kunming 650092，China)

A Lotka－Volterra two－species predator－prey system of population allelopathy with a discrete delay is studied.By linearizing the system at the positive equilibrium and analyzing the associated characteristic equation，the asymptotic stability of the positive equilibrium is investigated and Hopf bifurcations are demonstrated.Furthermore，the direction of Hopf bifurcation and the stability of the bifurcating periodic solutions are determined by the normal form theory and the center manifold theorem for functional differential equations.Finally，some numerical simulations are carried out for illustrating the theoretical results.

Lotka－Volterra predator－prey system;discrete delay;stability;Hopf bifurcation;periodic solution; allelopathy

O 175.13;O 193

A

1672－8513(2012)04－0286－06

10.3969/j.issn.1672－8513.2012.04.014

2011－12－19.

云南省自然科學基金(2011FZ086).

王新慧(1984－)，女，碩士.主要研究方向:微分方程與動力系統.

劉海鴻(1977－)，男，博士，副教授.主要研究方向:微分方程與動力系統.