基于二次傅里葉頻譜的運動模糊方向精確檢測

郭紅偉，田益民，付波

(1.紅河學院工學院，云南蒙自661100;2.北京印刷學院基礎部，北京102600; 3.湖北工業大學電氣與電子工程學院，武漢430068)

基于二次傅里葉頻譜的運動模糊方向精確檢測

郭紅偉1，田益民2，付波3

(1.紅河學院工學院，云南蒙自661100;2.北京印刷學院基礎部，北京102600; 3.湖北工業大學電氣與電子工程學院，武漢430068)

針對運動模糊圖像的模糊方向檢測問題，分析了運動模糊圖像的頻譜特性，提出基于二次傅里葉頻譜的運動模糊方向檢測方法.首先，對模糊圖像做2次傅里葉變換得到二次傅里葉頻譜;其次，對頻譜各像素按灰度值大小做排序，取排序第100的像素灰度為閾值使頻譜轉換為二值圖像;最后，過二值圖像中心作不同斜率的直線，通過計算所有亮點到直線的距離確定運動模糊方向.實驗數據顯示，該方法檢測運動模糊方向的精度高，且具有較強的抗噪聲能力.

圖像復原;運動模糊;點擴散函數;傅里葉變換

運動模糊圖像的復原是圖像復原中的重要課題之一，隨著科學技術的不斷發展，它在各個領域中的應用越來越多，要求也越來越高，可廣泛應用于天文、軍事、道路交通、醫學圖像、工業控制及刑偵領域，具有重要的現實意義.而圖像復原的關鍵在于點擴散函數(point spread function，PSF)的準確鑒別，若PSF已知，則可以用維納濾波、約束最小二乘方濾波等算法獲得復原圖像.運動模糊是由于拍照時相機與景物的相對快速運動導致同一時刻不同景物點在電荷藕合器件(charge－coupled device，CCD)的同一點同時曝光引起的，由于物體運動都有一定的慣性，在攝取圖像的短暫曝光時間內，一般可認為是勻速直線運動.勻速直線運動模糊的PSF由運動模糊方向和模糊尺度2個參數確定，對于模糊尺度的估算，文獻［1－4］均是以水平方向的運動模糊進行研究，因為任意方向的運動都可以通過圖像旋轉將模糊方向旋轉到水平軸方向.因此，運動模糊方向的精確檢測是估算模糊尺度和運動模糊圖像復原的關健.

近年來，出現了許多檢測運動模糊方向的方法，文獻［5－6］利用Radon變換檢測運動模糊圖像頻譜中的亮、暗條紋得到模糊方向;文獻［7］在此基礎上對頻譜先進行二值化再用Radon變換檢測，檢測精度有所提高;文獻［8］也是先對頻譜進行二值化，然后用霍夫變換檢測模糊方向;文獻［9－10］提出在空域對模糊圖像做不同角度微分后求和，最小值對應角度為模糊方向，其估計誤差較大，特別當模糊圖像紋理較少且存在大面積平滑區域時，將出現估計錯誤;文獻［11］利用運動模糊圖像倒譜的極小值(為負數)點坐標，采取幾何運算方式估算模糊方向;文獻［12］對倒譜取絕對值后用Radon變換鑒別模糊方向.以上文獻對運動模糊圖像做了大量研究，但是，運動模糊方向檢測的準確性，計算的高效以及方法的抗噪聲能力仍是值得關注的重點問題.

本文提出基于二次傅里葉頻譜的運動模糊方向檢測方法.通過對運動模糊圖像進行2次傅里葉變換，對二次傅里葉頻譜灰度值做排序，取某個排序灰度為閾值把頻譜變為二值圖像，計算二值圖像中亮點到過圖像中心直線的距離確定運動模糊方向.實驗數據顯示，該方法檢測運動模糊方向的精度高，能適用于小尺度運動模糊的模糊方向檢測，且具有較強的抗噪聲能力.

1 運動模糊圖像的頻譜特性

假設圖像f(x，y)有一個平面運動，令x0(t)和y0(t)分別為t時間內在x和y方向上運動的變化分量，T表示成相系統記錄介質的曝光時間.在不考慮噪聲影響的情況下，運動模糊退化圖像為:

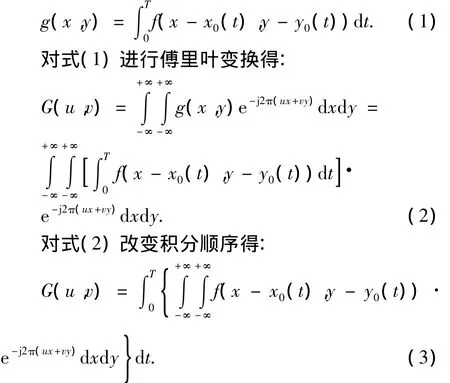
式(3)大括號內積分項是f(x－x0(t)，yy0(t))的傅里葉變換，由時移特性得:

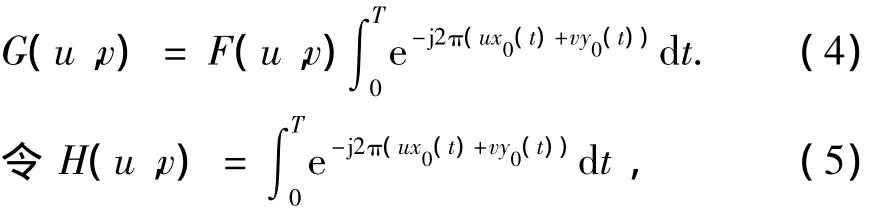
則得運動模糊圖像退化的頻域表述為:

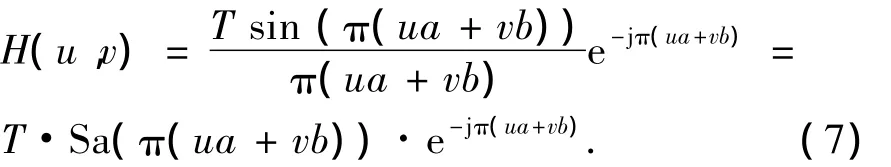
式(7)中Sa(π(ua+vb))稱作取樣函數，令γ= π(ua+vb)，則γ=0時取樣函數為最大值1，γ= nπ(n是不為0的整數)時函數值為0.所以，H(u，v)在(ua+vb)=0時取得最大值T，(ua+vb)為非0的整數時，H(u，v)等于0.原始圖像f(x，y)的傅里葉頻譜通常是各向同性的，能量主要分布在低頻區域.因此，由式(6)可知運動模糊退化圖像的頻譜中心會有一條較寬的亮帶，平行于亮帶兩邊將出現等間距的暗條紋，且越遠離中心，條紋特征越弱.圖1(a)、(b)是512×512像素的Lena原始圖像和運動模糊圖像(模糊尺度15像素，模糊角度45°).圖1(c)、(d)是它們對應的傅里葉頻譜圖，頻譜特征與理論分析一致.圖1(d)的亮、暗條紋剛好與運動模糊方向垂直，文獻［5－8］正是利用頻譜的這一特征估計運動模糊方向的.

圖像的紋理輪廓對應于傅里葉變換的高頻，圖像的平滑區域對應于傅里葉變換的低頻，取樣函數Sa(t)的傅里葉變換是一個門函數［13］:

F[]·表示傅里葉變換運算符.圖1(c)所示的Lena原始圖像頻譜較為平滑，因此對該頻譜再做1次傅里葉變換后，能量完全集中在低頻點上，如圖1(e)所示.圖1(d)所示的運動模糊圖像頻譜呈取樣函數Sa(t)的形式，故對該頻譜再做1次傅里葉變換后，能量集中在運動模糊方向上，如圖1(f)所示，二次傅里葉頻譜中出現1條與運動方向一致(45°)的亮條紋.需要說明的是:本節中的圖1(c)～(f)均是把頻譜0點移位到中心位置，且對頻譜值取對數壓縮灰度范圍后的顯示效果.由于二次傅里葉頻譜的特征集中在中心點附近，為突出這些特征，圖1(e)、(f)是剪切為192×192像素的顯示效果.

2 運動模糊方向檢測

由上節分析可知，在運動模糊圖像的二次傅里葉頻譜中有1條與運動模糊方向一致的亮條紋，本文通過檢測該條紋獲得運動模糊方向，為提高檢測精度，將對二次傅里葉頻譜進行二值化預處理.具體步驟如下:

1)計算退化圖像頻譜G(u，v)，并且移位使u= 0，v=0位于中心位置，為壓縮頻譜的灰度值范圍，取對數形式

2)對1)中結果重復相同步驟，得到運動模糊圖像的二次傅里葉頻譜，記作R(u，v);

3)對R(u，v)的各像素按其灰度值從大到小排序，記作Pn;取排序第100的像素灰度為閾值，把二次傅里葉頻譜轉換為二值圖像，記作B(u，v)，即:

4)過二值圖像中心(u0，v0)作不同斜率的直線，計算所有亮點到直線的距離并求和，最小值對應直線的傾斜角為模糊方向.對于大小為N×M的圖像，N、M為奇數時，中心點在(N+1)/2列和(M+1)/2行;N、M為偶數時，中心點在(N/2)+1列和(M/2)+1行.過點(u0，v0)，傾斜角為α的直線方程為:

設亮點坐標為(un，vn)，則亮點到直線的距離為:

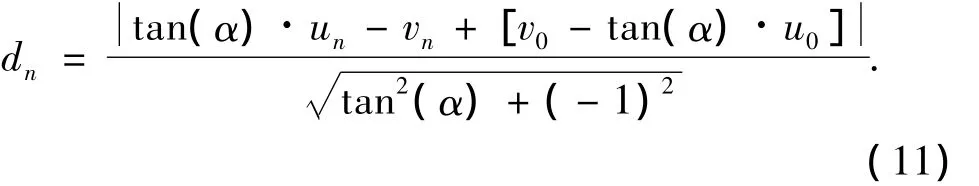
B(u，v)中所有亮點到傾斜角為α的直線距離之和為:

圖2(a)是由圖1(f)轉換的二值圖像，圖2(b)是α取－90°到+90°時對應的Sα曲線，Sα最小值對應α為45°，與實際方向一致.由于α為90°時，斜率不存在，編程實現過程中，α取90°應單獨處理，此時的

3 實驗分析

為驗證本文方法檢測運動模糊方向的有效性，采用256×256像素的Lena標準測試圖像進行仿真實驗.表1為在不添加噪聲情況下，對測試圖像做不同模糊尺度和不同模糊角度的運動模糊，然后用文獻［6］、［11］和本文算法進行模糊方向檢測的結果.數據顯示，模糊尺度較大時(如:20像素)，文獻［6］和［11］的檢測結果相對準確，檢測誤差不超過2°;模糊尺度小于10像素后，檢測誤差逐漸增大，文獻［6］的結果已不能反映運動模糊方向.而本文算法在模糊尺度較大時，能精確檢測出運動模糊方向，模糊尺度小于10像素時，檢測誤差也較小.

為驗證本文方法的抗噪聲能力，對Lena圖像做模糊尺度為20像素，模糊方向為45°的運動模糊，然后添加均值為0，方差從0.001到0.025的高斯噪聲.用文獻［11］和本文算法檢測不同強度噪聲污染圖像的模糊方向，圖3是對應的噪聲方差－檢測角度曲線.曲線顯示文獻［11］僅在噪聲方差小于0.002時能正確檢測出運動模糊方向，方差大于0.002后檢測結果嚴重偏離45°.本文算法在噪聲方差小于0.016時的檢測結果在45°左右，能正確反映運動模糊方向.

表1 512×512像素的Lena圖像實驗數據

4 結語

分析了運動模糊圖像的頻譜特性，揭示在運動模糊圖像的二次傅里葉頻譜中有1條與運動模糊方向一致的亮條紋，給出了檢測該亮條紋方向的精確數值計算方法.通過對Lena標準測試圖像的實驗數據證明，該方法檢測運動模糊方向精度高，能適用于小尺度運動模糊圖像的模糊方向檢測，且具有較強的抗噪聲能力.圖像長、寬不相等時，模糊圖像的一次傅里葉頻譜亮、暗條紋方向與運動方向不再垂直，而二次傅里葉頻譜中亮條紋方向始終與運動模糊方向一致，故利用二次傅里葉頻譜檢測模糊方向時無須要求測試圖像長、寬相等.

［1］張榮，楊建朝，張倩，等.SAR圖像運動模糊參數估計［J］.電子學報，2007，35(10):2019－2022.

［2］郭永彩，丁小平，高潮.基于差分自相關的運動模糊圖像尺度參數識別［J］.光電工程，2011，38(6):134－140.

［3］邸慧，于起峰.基于自相關的勻速運動模糊尺度參數識別［J］.國防科技大學學報，2006，28(5):123－125.

［4］賀衛國，黎紹發.勻速直線運動模糊長度的精確估計［J］.計算機應用，2005，25(6):1316－1317.

［5］MOGHADDAM M E，JAMZAD M.Finding point spread function of motion blur using radon transform and modeling the motion length［C］//Proceedings of the 4th IEEE International Symposium on Signal Processing and Information Technology.Italy:Rome，IEEE，2004:314－317.

［6］鄧澤峰，熊有倫.基于頻域方法的運動模糊方向識別［J］.光電工程，2007，34(10):98－101.

［7］李宇成，賈寶華，楊光明.運動模糊圖像的參數估計與恢復［J］.計算機工程與設計，2010，31(19):4247－4249.

［8］LOKHANDE R，ARYA K V，GUPTA P.Identification of parameters and restoration of motion blurred images［C］// Proceedings of the 2006 ACM Symposium on Applied Computing.USA:New York，ACM，2006:301－305.

［9］YITZHAKY Y，KOPEIKA N S.Identification of Blur Parameters from Motion Blurred Images［J］.Computer Vision Graphic Image Processing:Graphical Models and Image Processing，1997，59(5):310－320.

［10］陳前榮，陸啟生，成禮智.運動模糊圖像的運動模糊方向鑒別［J］.國防科技大學學報，2004，26(1):41－45.

［11］謝偉，秦前清.基于倒頻譜的運動模糊圖像PSF參數估計［J］.武漢大學學報:信息科學版，2008，33(2): 128－131.

［12］郭紅偉，朱家興，寸寧.基于倒譜分析的運動模糊參數估計［J］.云南民族大學學報:自然科學版，2012，21 (2):150－153.

［13］吳大正，楊林耀，張永瑞，等.信號與線性系統分析［M］.4版.北京:高等教育出版社，2005:145－146.

(責任編輯莊紅林)

Accurate Detection of the Motion Blurred Direction Based on Twice Fourier Spectrum

GUO Hong-wei1，TIAN Yi-min2，FU Bo3
(1.Engineering School，Honghe University，Mengzi 661100，China; 2.Department of Basic Science，Beijing Institute of Graphic Communication，Beijing 102600，China; 3.School of Electrical and Electric Engineering，Hubei University of Technology，Wuhan 430068，China)

Aiming at solving the problem related to the blurred direction of motion blurred image，the spectrum characteristics of the motion blurred image were analyzed and a method for detecting the motion blurred direction based on twice Fourier spectrum was proposed.Firstly，the twice Fourier spectrum of blurred image was calculated.And then all pixels from big to small in the spectrum were sorted out by grayscale value，the 100th largest grayscale value was selected to be a threshold to transform the spectrum to a binary image.Finally，by drawing straight lines of all slopes through the center of the binary image，the motion blurred direction was ascertained by calculating the distances from all bright spots to the straight line.The experiment results show that the method has high accuracy and good anti－noise ability.

image restoration;motion blur;point spread function;Fourier transform

TP 391

A

1672－8513(2012)04－0301－04

10.3969/j.issn.1672－8513.2012.04.018

2011－12－25.

國家自然科學基金(61178092，61072130).

郭紅偉(1980－)，男，碩士，講師.主要研究方向:數字圖像復原.