曲線插值的一種具有還圓性的細分方法

韓 靖， 韓旭里

（中南大學數(shù)學科學與計算技術學院，湖南 長沙 410083）

插值細分方法是一種離散數(shù)據(jù)插值，是計算機輔助幾何設計中用于曲線曲面表示的重要方法。由于細分方法通常沒有顯式表達式，僅提供一個算法描述過程，具有簡單、高效等特點，所以特別適用于計算機表示。近年來，細分方法引起越來越多的關注。

傳統(tǒng)細分方法有切割磨光法和四點插值法，已經有許多學者作了相關研究[1-10]。切割磨光法是逼近型細分方法，具有逼近性，光滑性，保凸性等優(yōu)點，其中Chaikin方法已被證明其極限曲線是由已知控制多邊形所定義的二次 B樣條曲線[1-2]，但其極限曲線不經過控制頂點。文獻[3]中的四點插值細分法，極限曲線可以表示三次B樣條曲線。二次B樣條曲線和三次B樣條曲線作為分段多項式曲線，不能精確表示橢圓曲線。四點插值法是線性細分方法，簡單易懂，但沒有考慮控制多邊形的幾何形狀，單從解析角度構造新點，不易對曲線的幾何形狀進行控制[8]，且其極限曲線上可能有多余的拐點等[7]。

近年來，細分方法對保形性作了許多研究。為了使產生的細分曲線具有更好的保形性，文獻[11]提出了一種基于法向量的細分方法，可以證明這種方法產生的曲線G1連續(xù)，只要選取合適的參數(shù)，此方法為保形細分算法，而且具有許多優(yōu)美的性質，例如：可以插值在指定點的法向量、可以生成圓錐曲線、直邊等。文獻[12]提出了一種基于切向的幾何插值型保凸細分方法，在細分的過程中，每條邊所對應的新控制頂點由原控制頂點及其切向確定。該方法產生的極限曲線是G1連續(xù)的，且較為美觀。由于保凸等性質對于線性細分較難達到，目前，非線性細分方法已成為研究的重點內容。

本文針對傳統(tǒng)線性細分方法不能表示圓等非多項式曲線的情況，基于控制頂點的幾何關系提出一種新的四點細分方法，如果初始控制頂點都取自同一個圓上，那么本方法所得極限曲線就是這個圓。

1 基于幾何特性的四點細分法

細分法是通過不斷地加入新點構造細分曲線。給定初始點列 {}i，四點插值型細分方法為

其中G表示一種構造，G的選取，也就是如何選擇是插值細分方法的關鍵。

我們知道，過不在同一直線上的相鄰三點可以作一個圓。這樣，過相鄰二插值點的圓弧有兩條。我們的方法是取這兩條圓弧的中點，將其加權平均得到新插值點。

1.1 計算插值點

對于第k層的點列{}，若3點i不共線，則它們確定一個圓，記為。為邊與邊的垂直平分線 的交點，滿足

得到新插值點，其中ω為權數(shù)，可用于調整曲線的形狀。

結合式(2)～(7)即為式(1)中的函數(shù)G。

對于第k層的點列{，設第k層節(jié)點總數(shù)是n。當要生成封閉曲線時，點即；點。若要生成的曲線是開曲線，計算時，可用。這樣保證了方法的可行性，也充分提取了控制頂點的信息。

圖1 計算插值點

1.2 算法描述

作圖時，新點的數(shù)量不需要無窮多，只需達到曲線在視覺上連續(xù)即可。定義Δ為任意相鄰兩點間的最大距離（包括初始點和最末點之間的距離）的上限，當點列中任意相鄰兩點間的距離都小于Δ時，曲線即達到視覺上連續(xù)，Δ的取值依賴于顯示設備。該細分方法可用如下算法過程描述：

步 0 給定有0n個頂點的初始封閉凸多邊形頂點點列及權數(shù)ω，令 :k= 0。

步 1 若要生成閉曲線，則令

顯然，當所有初始控制頂點都取自同一個圓上時，新的插值點仍然在這個圓上，因此，本文的方法具有還圓性。

2 數(shù)值實例

作數(shù)值實例分析將本文方法與經典的切割磨光法與四點插值法以及文獻[12]提出的基于幾何切向的六點插值細分法對比作對比，其中切割磨光法取 Chaikin算法，即==1/4，細 分規(guī)則是

其中，N是初始頂點個數(shù)。四點插值法采用Dubuc格式[9]

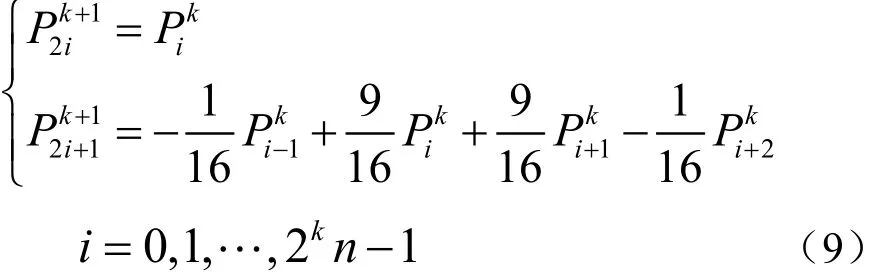
文獻[12]提出了一種基于幾何切向的六點插值型細分方法，具有還圓性，以及保凸性等性質。

例1 取初如控制頂點(-1, -1), (0, 0), (0.5, 0),(1.8, 0), (3.2, 0.5), (4, -1)，3點(0,0), (0.5,0), (1.8,0)共線，用本文方法取0.5ω=，曲線見圖2，共線3點之間并非直線。曲線在共線點間的形狀取決于相鄰不共線點的偏離程度，偏離得越近，曲線越趨于直線。

圖2 本文方法例1

例 2 取初始控制頂點(1,0), (0,1), (-1,0),(0,-1)，生成閉曲線。分別用本文方法取0.5ω=和經典的切割磨光法與四點插值法的Dubuc格式，曲線見圖3、圖4、圖5。可見本文的方法可以完整的還圓，這從方法的推導過程也可得出，若所有初始點都在同一圓上，則相同，進而也與相同，都是圓上的點。切割磨光法與四點插值法都不具有還圓性。

圖3 本文方法例2

圖4 切割磨光法例2

圖5 四點插值法例2

例3 取初始控制頂點(0,0), (0.2425,1.3751),(-2.6241,0.9551), (-2.0944,-3.6276), (4.2784,-3.5900),(5.3480,4.4875), (-4.1888,7.2552), (-9.1844,-3.3429),(1.9397,-11.0004)，用本文方法取0.5ω=和切割磨光法繪制開曲線，見圖 6、圖 7。本文方法可繪制出曲率半徑變化比較光滑的螺旋，切割磨光法繪制曲線不經過控制頂點，曲線的曲率半徑變化也不光滑，曲線形狀更趨向控制多邊形。

圖6 本文方法例3

圖7 切割磨光法例3

例4 給定初始控制多邊形頂點為(3.0000,0),(0.3090,0.9511), (-0.8090,0.5878), (-0.8090,-0.5878),(0.3090,-0.9511)，采用本文方法取0.2ω=、四點插值法和文獻[12]提出的細分法繪制曲線，如圖8、圖9所示。與文獻[12]的方法相比，本文方法的極限曲線更靠近控制多邊形。

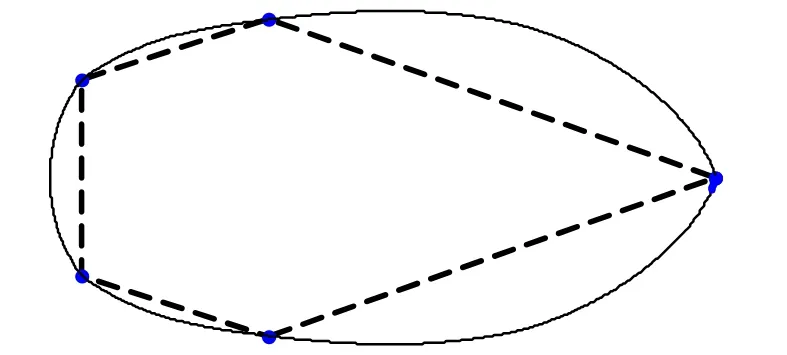
圖8 本文方法例4

圖9 文獻[12]的方法例4

例 5 設初始控制頂點(1.0,1.0), (1.2,2.1),(2.0,2.5), (2.5,1.8), (3.0,1.5), (3.4,2.6), (4.0,3.2),(4.4,3.1), (5.0,2.0)，用本文方法，分別取ω=0.3，ω= 0 .7繪制曲線。結果見圖10、圖11。對比可知ω取值越小，曲線越靠近控制多邊形，但光滑性不佳；當ω增大，曲線遠離控制多邊形，且較為圓滑。

圖10 例5中ω=0.3

圖11 例5中ω=0.7

3 結 論

本文針對傳統(tǒng)細分方法不能表示圓等非多項式曲線的限制，基于幾何提出了一種含有一個參數(shù)的四點插值細分方法。這種方法的推導比較簡單，給出了插值點計算公式和算法描述。與切割磨光法和四點插值法相比，本文的方法具有還圓性，可以實現(xiàn)保凸性，極限曲線較光順。參數(shù)可以控制曲線與控制多邊形的接近程度，參數(shù)取較小值時曲線靠近控制多邊形。

由于本文提出的計算公式是一種非線性表示，方法的收斂性，光滑性等證明和與參數(shù)取值的關系還需要進一步研究。參數(shù)為0時曲線保凸這一條件較為嚴格，參數(shù)的取值范圍應與保凸性具有某種關系。這些是接下來工作的重點。

[1]Chaikin G M. An algorithm for high speed curve generation [J]. Computer Graphics and Image Processing, 1974, 3(4): 346-349.

[2]Riesenfeld R F. On Chainik’s algorithm [J]. IEEE Computer Graphices and Applications, 1975, 4(3):304-310.

[3]Catmull E, Clark J. Recursively generated B-spline surfaces on arbitrary topological meshes [J].Computer Aided Design, 1978, 10(6): 350-355.

[4]Hassan M F, Ivrissimitzis I P, Dodgson N A, et al. An interpolating 4-point C2 ternary sationary subdivion scheme [J]. Computer Aided Geometric Design, 2002,19(5): 1-18.

[5]Dyna N, Levina D, Liu D. Interpolatory convexity-preserving subdivision schemes for curves and surfaces [J]. Computer-Aided Design, 1990,24(4): 221-216.

[6]Méhautéa A L, Utreras F I. Convexity-preserving interpolatory subdivision [J]. Computer Aided Geometric Design, 1994, 11(1): 17-37.

[7]Marinov M, Dyn N, Levin D. Geometrically controlled 4-point interpolatory Schemes [C]//Neil D,Michael S F, Malcolm S. Advances in Multiresolution for Geometric Modelling. London:Springer-Verlag, 2005: 301-315.

[8]Dyn N, Levin D, John A. A 4-point interpolatory subdivision scheme for curve design [J]. Computer Aided Geometric Design, 1987, 4(4): 257-268.

[9]Dubuc S. Interpolation through an iterative scheme [J].Journal of Mathematical Analysis and Applications,1986, 114(1): 185-204.

[10]曹 沅. 四點插值細分算法極限曲線曲面C2連續(xù)的充分必要條件[J]. 計算機輔助幾何設計與圖形學學報, 2003, 15(8): 961-966.

[11]Yang Xunnian. Normal based subdivision scheme for curve design [J]. Computer Aided Geometric Design,2006, 23(4): 243-260.

[12]鄧重陽, 汪國昭. 曲線插值的一種保凸細分方法[J].計算機輔助設計與圖形學學報, 2009, 21(8):1042-1046.