吉林省各高校本科組數學建模競賽成績評價與預測

曹忠威

(吉林財經大學 應用數學系，長春 130017)

0 引言

數學建模是聯系數學與實際問題的橋梁，是數學在各個領域廣泛應用的媒介，是數學科學技術轉化的主要途徑。數學建模在科學技術發展中的重要性越來越受到數學界和工程界的普遍重視，它已成為現代科技工作者必備的重要能力之一。

在數學建模網站中獲取吉林省賽區十一五期間的各院校數學建模成績。如果從多個因素著手就會脫離客觀現實，具有不可操作性。因此，我們只著眼于學校數學建模綜合成績、優秀率和學習基礎。首先，我們選定每年數學建模競賽綜合成績、學習基礎和優秀率作為影響數學建模狀況評價的因素，并對每個因素進行賦權;然后，通過建立評判矩陣，計算出每個院校的評價得分，可以用此方法來評價數學建模獲獎狀況的排名。

1 模型假設與符號說明

1.1 模型假設

①假設每年的試題難度沒有太大差別。②假設成功參賽獎對數學成績無影響。③假設每年參加比賽學生的學習能力基本不變。④假設每個學生處于相同的試題環境中。⑤假設樣本數據真實可靠，忽略人為計算誤差。⑥假設所取樣本數據在一定時間內保持穩定，具有典型代表性。

2 模型建立與求解

2.1 建立層次模型

我們將影響數學建模成績因素問題分解成三個層次，最上層為目標層，即數學建模競賽成績;中間層為準則層，優秀率C1、綜合成績C2、學習基礎C3三個因素。最下層為指標層，即五個指標國家一等獎P1，國家二等獎P2，省一等獎P3、省二等獎P4、省三等獎P5。

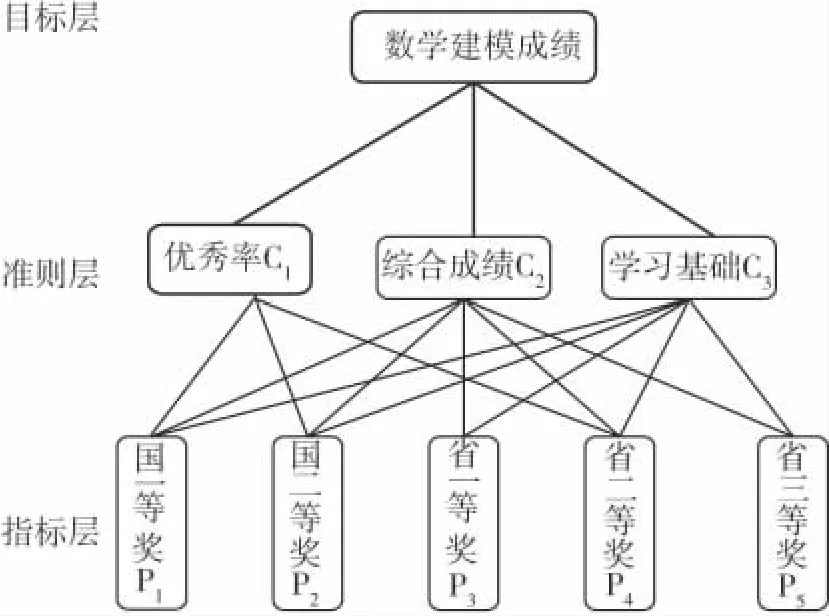
2.2 模型求解

假設以上一層次元素U為準則，所支配的下一層次的關系為C1，C2，C3我們的目的是要按它們對于準則U的相對重要性賦予C1，C2，C3相應的權重。因此我們采用比較法和平均一致性指標確定原則，見文獻［1］。

根據尺度aij的取值原則，我們得到判斷矩陣U-C:將準則層C中的三個因素C1，C2，C3兩比較，得成對比較矩陣。運用Matlab程序求出相應矩陣的最大特征λmax，并求出其對應的特征向量，即為權重矩陣［2］。

利用Matlab編寫程序，計算U-C矩陣的特征值，容易解 λmax=3.0291和權重向量A=(0.659，0.098，0.243)T，由公式得CI=0.01455.當n=3時，隨即一致性指標RI的值為0.52，于是CR=0.0279＜0.1.通過了一致性檢驗。根據尺度aij的取值原則，我們得到判斷矩陣C1-P、C2-P及C3-P。

U－C判斷矩陣

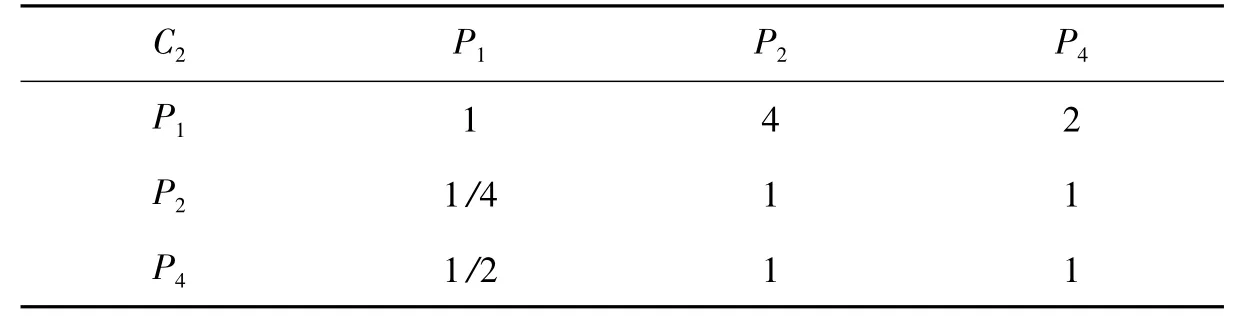
C1－P判斷矩陣

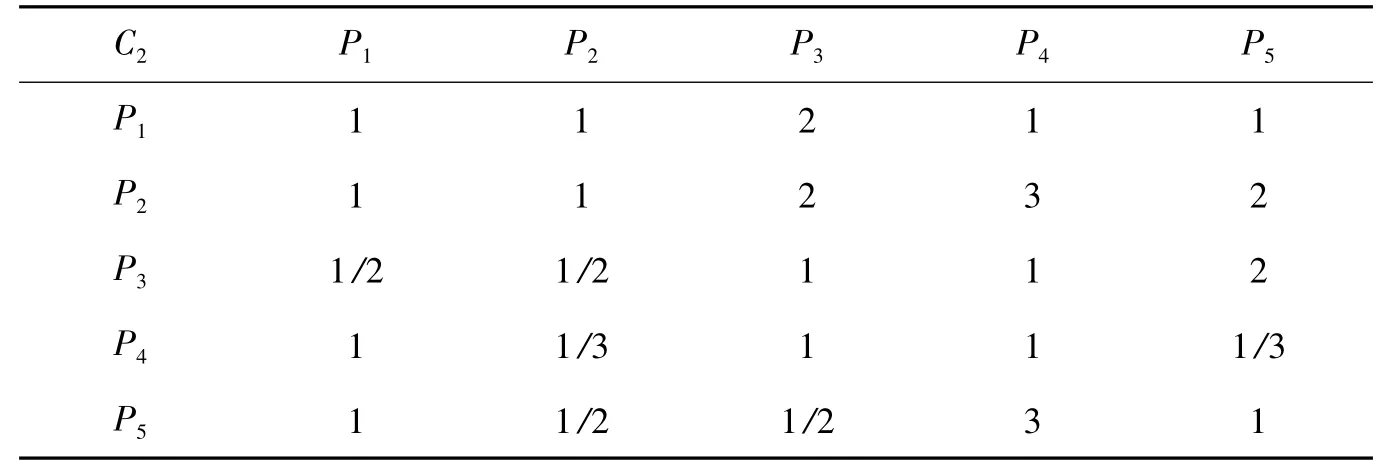
C2－P矩陣

C3－P矩陣

將由上述的四個判斷矩陣計算出的權重向量A，最大特征值λmax和一致性指標CI列入表中，其中C為判斷準則，P為要指標，P1為獲國家一等獎，P2為獲國家二等獎，P3為獲省一等獎，P4為獲省二等獎指標，P5為獲省三等獎指標。

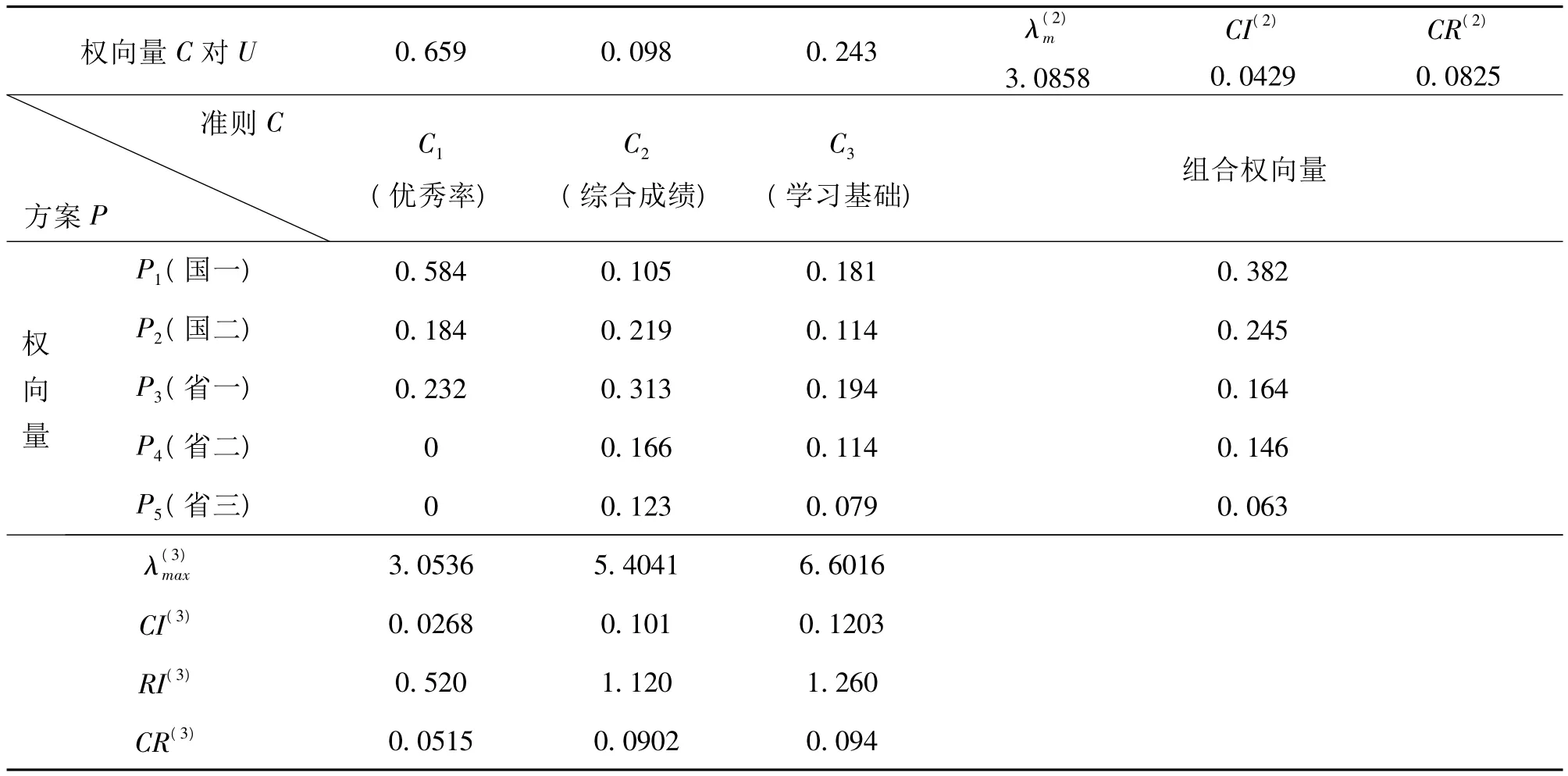
表1 數學建模競賽影響力計算結果

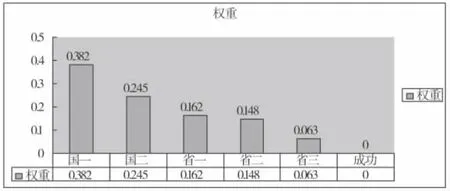
圖1 影響數學建模成績指標權重

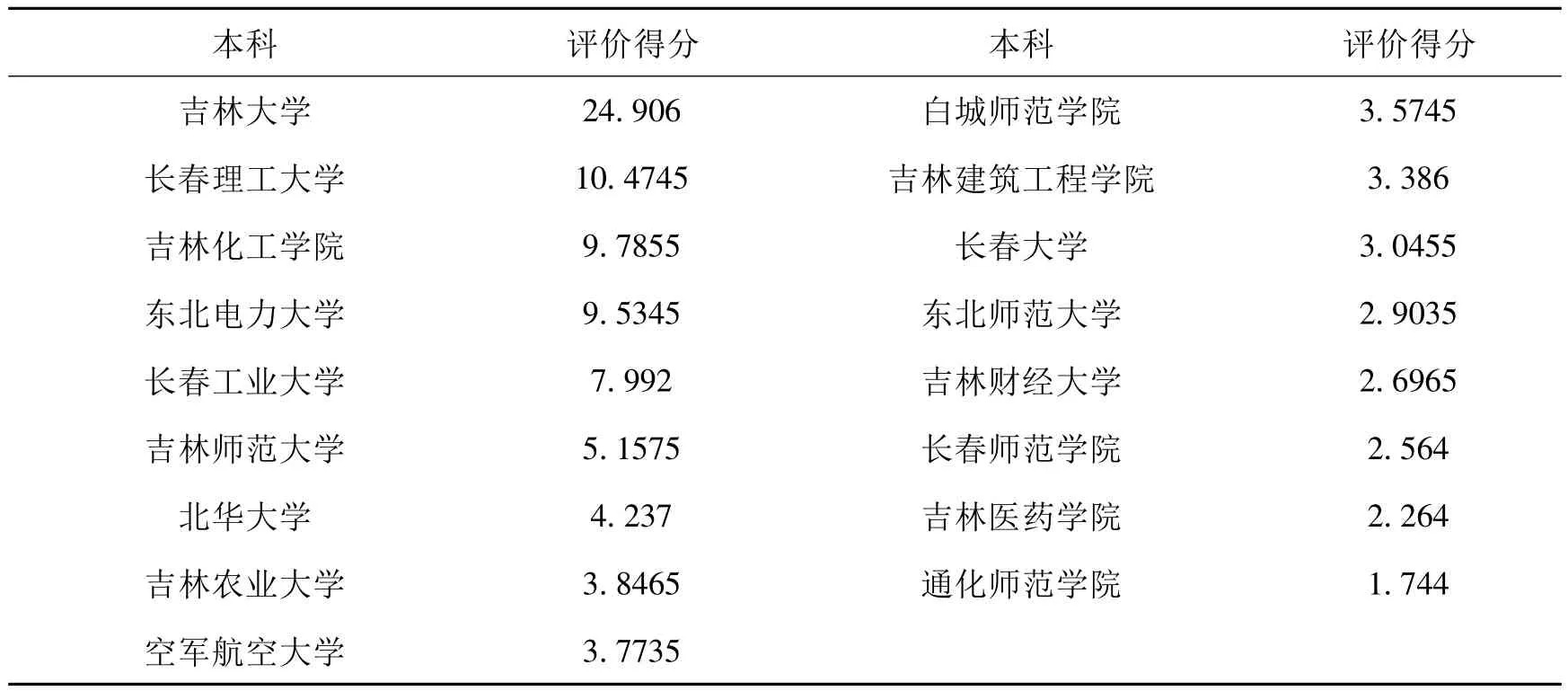
表2 吉林賽區本科組參賽院校競賽成績排名

首先，國家一等獎對數學建模成績產生的影響最大，權重為0.382;其次，國家二等獎指標權重為0.245，對數學建模成績的影響也比較大;省一等獎、省二等獎的指標，分別為0.162和0.148，對數學建模成績的影響略低于前兩項;最后，省三等獎影響相對于其他幾項較小，它的權重為0.063。結合得出的權重，我們得到如下的吉林省各高校數學建模成績排名。

從上表中我們可以知道，在本科組中排名前五的學校有:吉林大學、長春理工大學、吉林化工學院、東北電力大學、長春工業大學、吉林大學、長春理工等三所學校的評價得分較高，在吉林省賽區名列前茅，同時也說明了吉林大學、長春理工大學、吉林化工學院等院校師資力量非常雄厚，并且對數學競賽活動工作十分重視。

［1］韓中庚.數學建模方法與應用［M］.北京:高等教育出版社，2版.2005.6.

［2］劉宏.綜合評價中指標權重確定方法的研究［J］.河北工業大學學報，1996(4):44-46.

［3］阮曉青.數學建模引論［M］.北京:高等教育出版社，2005.

［4］朱少平.企業競爭力評價指標體系及模糊判斷［J］.陜西經貿學院報，2002(5):57-58.

［5］胡曉冬.matlab從入門到精髓［M］.北京:人民郵電出版社，2010.