智能切換的模型參考模糊自適應內模控制的研究

葉文通，陳 勇，祝永華

(衢州學院，浙江 衢州 324000)

1 引言

從我國發電狀況來看，水力和核能發電發展很快，但由于火電發電具有投入少，工期短和見效快等優勢，所以，火電發電還承擔著主要的發電任務。而火電發電會涉及到發電安全和穩定高效運行等重要問題。發電廠中單元機組的大容量、高參數、高效率的發展趨勢，必然會要求機組的控制系統要有較高的的控制品質和高水平的自動化程度。而大滯后、大慣性、非線性和擾動頻繁等是單元機組具有的特征，運用常規控制方法已很難滿足電網對機組的要求，必然要求火電控制中采用先進的智能化控制方法如：模糊、預測控制、內模控制等智能控制策略。在控制實現時，由于操作機構等的限制，控制信號的幅度及其變化率會被限制，因此必然要求在設計控制器的時候考慮控制受限的問題。文獻中有利用柔化濾波器來限制控制量幅值、延長調節時間使控制量最小化等，但系統響應的快速性必然受到影響。Garcia等利用線性規劃、二次規劃等來處理，但算法復雜，實現困難。

因此，本文采用模型參考自適應控制的思想，結合模糊控制方法和內模控制方法，提出了一種模型參考模糊自適應內模控制方法：在相消法設計內模控制器的基礎上，利用參考模型的系統誤差及其變化率去調節控制器中的參數。并用帶反饋校正的模型預測作系統輸出預測，根據系統響應和系統預測值是否在給定誤差范圍內來共同決定控制量在限幅值與內模控制器輸出值之間進行在線智能切換。并通過熱工對象的魯棒性仿真研究，證明其有效性。

2 模糊推理的模型參考自適應內模控制系統設計

2.1 控制系統結構

在相消法設計內模控制器的基礎上，利用參考模型的系統誤差及其變化率去調節控制器中的參數如圖1所示。

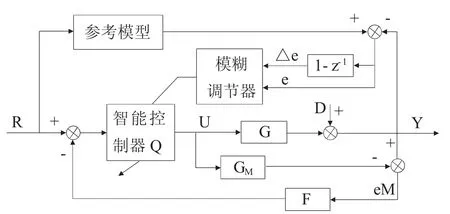
圖1 自適應內模控制系統

其中，G為原始的被控對象，GM為其模型，GC是智能控制器，F為反饋濾波器，R、D和Y分別為輸入、擾動及輸出，eM、e和△e分別為模型誤差、系統誤差及其變化率。

2.2 控制器的設計

在GM準確的情況下我們可以通過對偶性來判斷閉環系統的穩定性。

用相消法設計GC的思路是，將GM分解為兩部分，即：GM（z）=GM+（z）GM-（z），其中，GM（z）是實際連續過程模型的傳遞函數加零階保持器再離散化后得到的系統模型，GM+是模型的最小相位部分，GM-是模型的非最小相位部分。

則內模控制器GC為其中f為可實現因子，即控制濾波器，通常設一階濾波器為

由對偶穩定性可知，GC穩定則閉環系統也穩定。而且GC能保證系統對階躍輸入和擾動穩態無差。

2.3 模糊參數調節器設計

系統誤差e及其變化率△e，分別記為E，EC為輸入變量；控制器參數α為輸出變量。取E和EC的論域均為[－6，6],用X和Y表示：

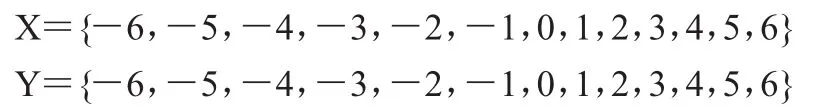
α 的論域分 5 檔，用 Z表示：Z＝{1，2，3，4，5}

子集記為：

E和EC及α的各模糊子集的隸屬度函數見表1和模糊規則控制表如表2所示。

表1 E和EC的各模糊子集的隸屬度函數

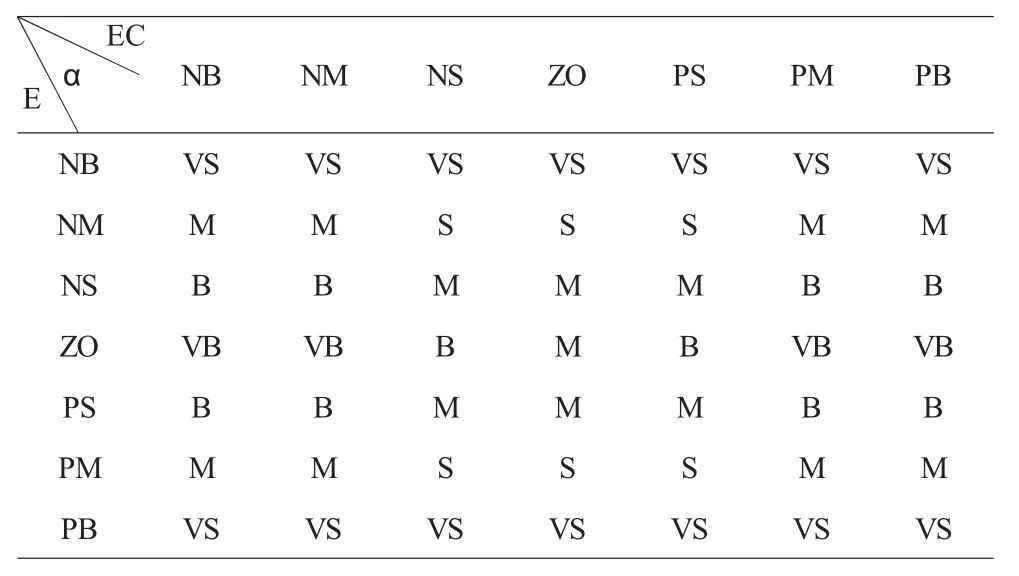
表2 模糊控制規則表

采用加權平均法對輸入數據進行模糊化如表3所示。

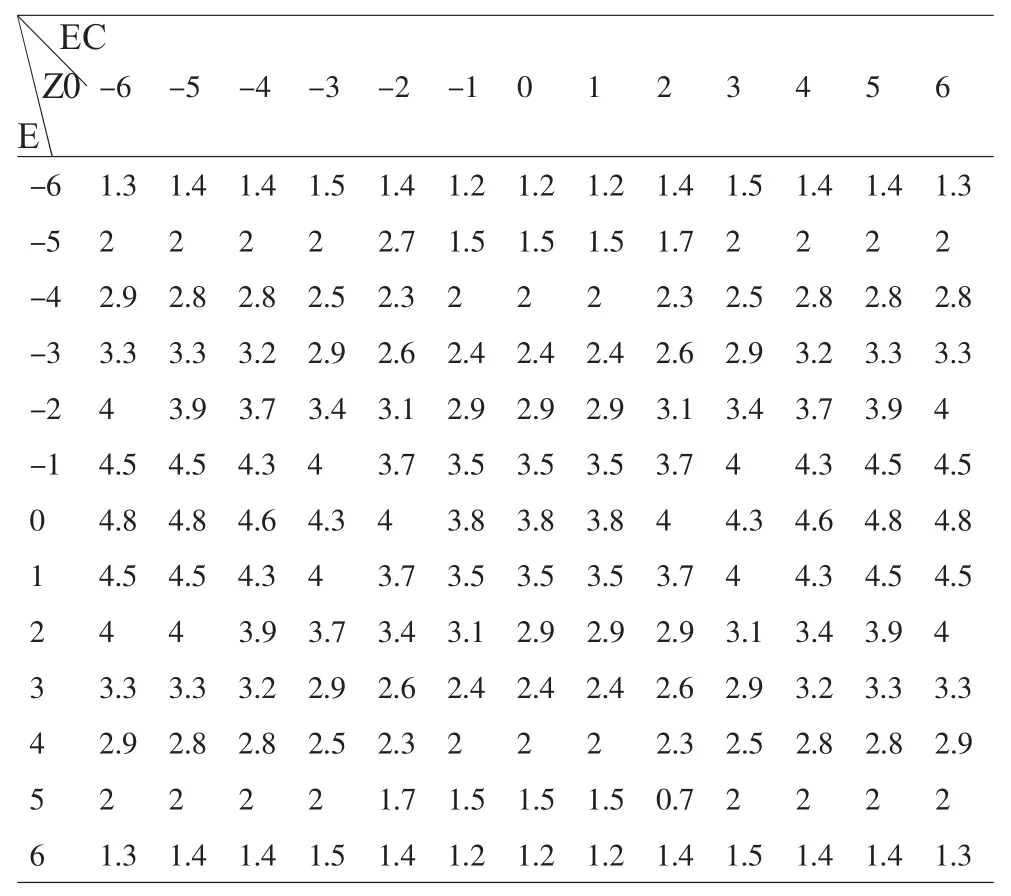
表3 模糊參數整定表

2.4 智能控制器的整定

智能控制器的系統結構圖如圖2所示。

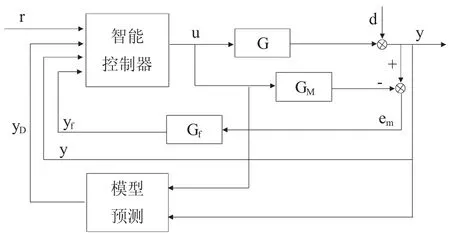
圖2 智能內模控制結構圖

如圖3，令y1和y2分別為系統誤差帶的下、上限,y1'和y2'分別為系統預測輸出的上、下限，y1、y2、y1'、y2'均可在線調整；y p(k+L)為系統模型預測輸出值，其L表示滯后步數。

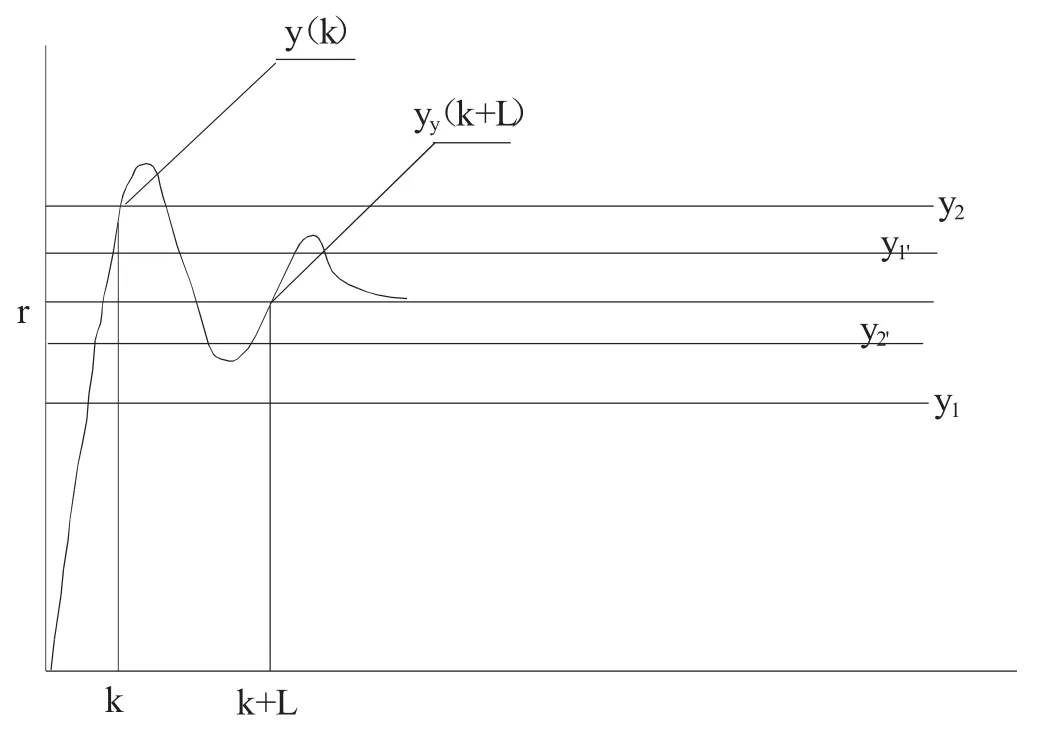
圖3 輸出與誤差關系

采用對控制器的輸出采用分段計算的方法，控制規則如下:

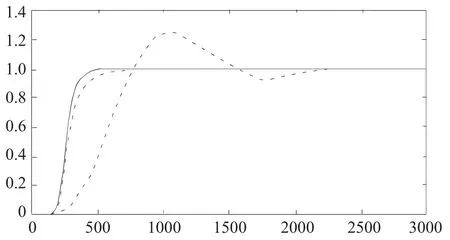
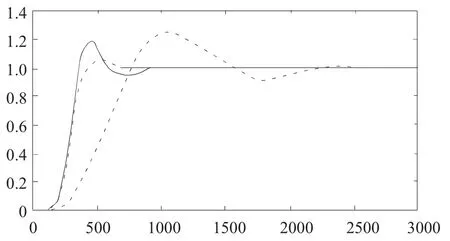
①y(k)

②y(k)>y2且yp(k+L)>y2'，按最小限幅值計算u(k)；

③其他均按式y=Gr×r+Gd×d=r計算控制量u(k)。

3 在線智能切換的模型參考模糊自適應內模控制在過熱汽溫中的應用

針對國內某500MW火電廠鍋爐過熱器一級減溫被控對象動態傳遞函數進行在線智能調節的模型參考自適應內模控制系統仿真，并與常規內模控制系統、PID控制系統作各種性能比較。

一級減溫控制系統被控對象的比例系數基本隨著負荷增大而增大，而時滯常數基本隨著負荷的增大而減小。文[8]由階躍響應曲線來擬和求取傳遞函數，采用兩點法，則被控對象的傳遞函數為

當 0≤u(k)≤2，取 α=0.6，在模型不變時，y1=0.75、y1'=1.8、y2=1.17、y2'=1.11，當參數發生變化時，y1=0.68、y1'=1.04、y2=1.28、y2'=0.83。

圖中實線是為在線智能切換的模型參考自適應內模控制的響應曲線，小虛線是常規內模控制的響應曲線、大虛線是PID控制的響應曲線。

圖4 模型匹配仿真結果

圖5 模型不匹配仿真結果

仿真結果表明，在模型匹配時，PID控制系統的響應速度太慢，控制效果較差，而常規內模控制和在線智能切換的模型參考自適應內模控制能達到較好的控制效果；在模型失配時（K增大20%，滯后時間減小10%），PID控制較差，在線智能切換的模型參考自適應內模控制和常規內模控制相比較，不僅同樣具有良好的快速性，而且超調小，魯棒性好。

4 結語

文章在總結自由度內模控制的調節方法和規律的基礎上，在相消法設計內模控制器的基礎上，利用參考模型的系統誤差及其變化率去調節控制器中的參數。并用帶反饋校正的模型預測作系統輸出預測，根據系統響應和系統預測值是否在給定誤差范圍內來共同決定控制量在限幅值與內模控制器輸出值之間進行在線智能切換。并通過熱工對象的仿真研究結果表明，這種方法可以使系統的性能達到快速性和魯棒性的最佳結合。其參數的在線調節的方法簡單實用，具有一定的工程應用價值。

[1]Garcia C.E.,Morari.internal model control.A unifying review and some new results I&EC Process Des.Dev.,1982,21(2):308-323

[2]趙曜.內模控制發展綜述[J].信息預控制，2000，29（6）：526～531.

[3]趙耀.直流調速系統的2自由度內模控制方法[J]電氣傳動，1997，27（1），41-43.

[4]張井崗，吳聚華，曾建潮.模型參考自適應內模控制及其仿真研究[J].系統仿真學報，1997，9（2）：38-43.

[5]李成鑫.有控制限幅的模型參考模糊自適應內模控制研究:[D].四川:四川大學，2006.

[6]金小崢，楊尤紅.考慮有執行器故障和有界擾動的魯棒自適應容錯補償控制(英文)[J].自動化學報，2009，（3）.

[7]柴天佑,張亞軍.基于未建模動態補償的非線性自適應切換控制方法[J].自動化學報，2011，（7）.

[8]郭巨眾.模糊內模控制模糊內模控制及其在過熱汽溫控制中的應用[D].太原：太原理工大學，2006.