柔性制造環境下AGV車輛規模仿真優化研究＊

陶翼飛 陳君若 劉美紅 傅亞力

（昆明理工大學機電工程學院1） 昆明 650093） （昆船設計研究院2） 昆明 650051）

0 引 言

自動導向小車 （automatic guided vehicle，AGV）系統以其自動裝卸載能力，靈活的路徑選擇，容易改變路徑和控制成為柔性制造系統（flexible manufacturing system，FMS）中物流系統的最佳選擇.通過對AGV系統的靈敏度分析顯示車輛規模是AGV系統各要素中對柔性制造系統影響最大的環節［1］.在AGV系統設計的過程中需要確定適當的車輛規模，充足的車輛規模可以及時完成任務，但是從經濟利益考慮AGV不宜過多，同時還會加劇AGV系統的車輛擁堵［2］.

目前AGV系統車輛規模研究主要分為3類：（1）確定型，主要用于AGV系統規劃階段，通過建立線性規劃、網絡模型對車輛規模進行求解，這種方法求解較容易，但建立模型往往對實際問題進行了簡化，不容易得到最優解［3］；（2）隨機型，如排隊模型，約束條件與實際問題相似，但求解困難［4］；（3）仿真型，通過仿真軟件、Petri網等建立AGV系統仿真模型，進行仿真實驗得到最優解，這種方法的優點是模型能夠得到最優解且可靠性高，缺點是建模過程和仿真實驗耗費時間，仿真成本較高［5］.

本文提出首先通過經典數學模型對AGV系統車輛規模進行估算，以估算結果確定初始仿真實驗輸入變量取值范圍，對仿真結果進行方差分析，根據分析結果進行優化算法與仿真模型的迭代，最終得到最優解.通過估算模型決定初始仿真實驗的輸入變量，同時在模型求解的過程中融入仿真優化思想，有效提高了求解效率和精度.

1 仿真優化

仿真優化過程描述如下：首先由優化算法產生初始解（決策變量），然后將其輸入仿真模型中，仿真運行結束輸出響應值（性能指標），通過數據轉換接口將其反饋到優化算法中，作為優化算法確定新一輪搜索方向的依據，并將搜索結果重新輸入仿真模型.上述過程反復進行，直至滿足預先設定的終止條件.常見的仿真優化過程模型見圖l［6］.

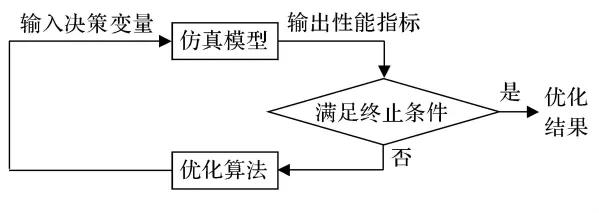
圖1 仿真優化模型

2 系統構成

2.1 估算模型

Egbelu提出AGV系統車輛規模的計算模型（式（1）～（5）中各參數表示意義，見表1），即通過非仿真的方法計算制造系統的車輛需求，在文獻中證明該模型在各種調度方法中能夠得到比較好的估算值.由于該模型是用解析的方法計算AGV系統車輛規模的一般模型，具有通用性，但是針對具體的系統約束條件有一定的誤差，因此本文采用該模型作為估算模型，得出估計值，以確定仿真實驗輸入變量取值范圍.加入估算模塊可以確定初始仿真實驗范圍，有效減少仿真與優化算法的迭代次數，提高系統求解效率.

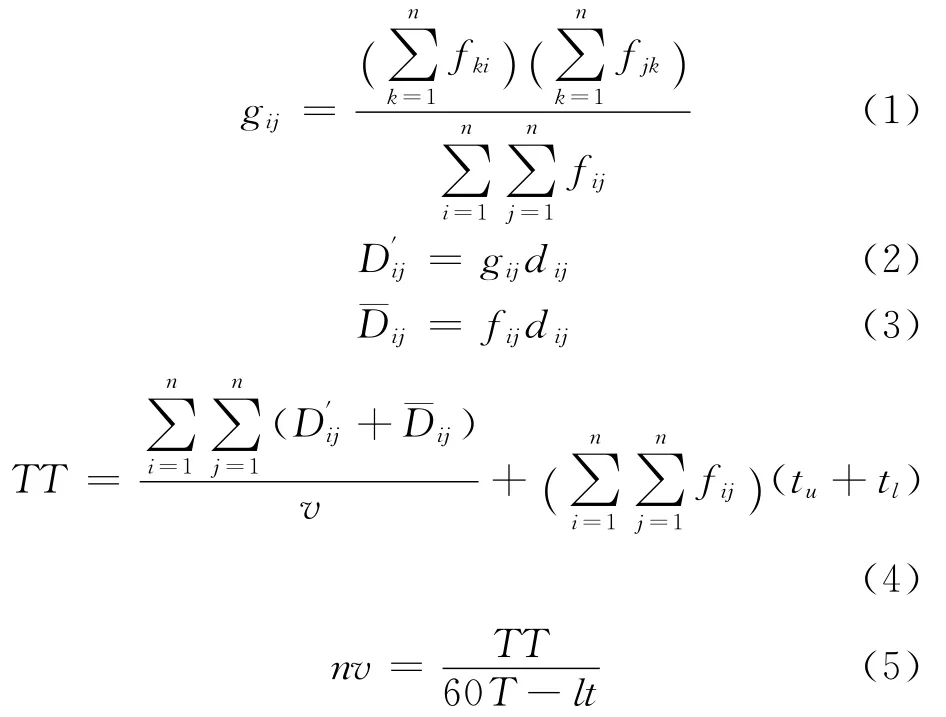
表1 各參數表示意義

2.2 仿真模型

2.2.1 模型建立 利用面向對象的仿真建模框架對柔性制造系統中的對象特征、對象行為及其之間的相互關系來進行系統建模，根據柔性制造系統的運行特點，面向對象的仿真系統由以下5大類對象構成：（1）實體類對象 加工中心、工件、路線等；（2）信息類對象 生產計劃、庫存信息、生產周期等；（3）控制過程類對象 物流控制、生產過程控制、生產調度等；（4）過程分析類對象 瓶頸分析、結果方差分析；（5）結果類對象 仿真結果顯示.

2.2.2 調度方法及運行機理 仿真系統運行時，以生產計劃等信息類對象作為主線，生產調度等控制過程類對象的控制為指導，操作對象即仿真實體類對象如工件由仿真時鐘進行狀態切換.具體過程為：系統運行時，實體類對象根據不同的控制策略由仿真時鐘觸發，形成離散系統的仿真事件，并相應改變實體的運行狀態，通過物流資源的運輸，形成實際的柔性制造過程.在本研究中柔性制造系統工作調度方式流程見圖2.

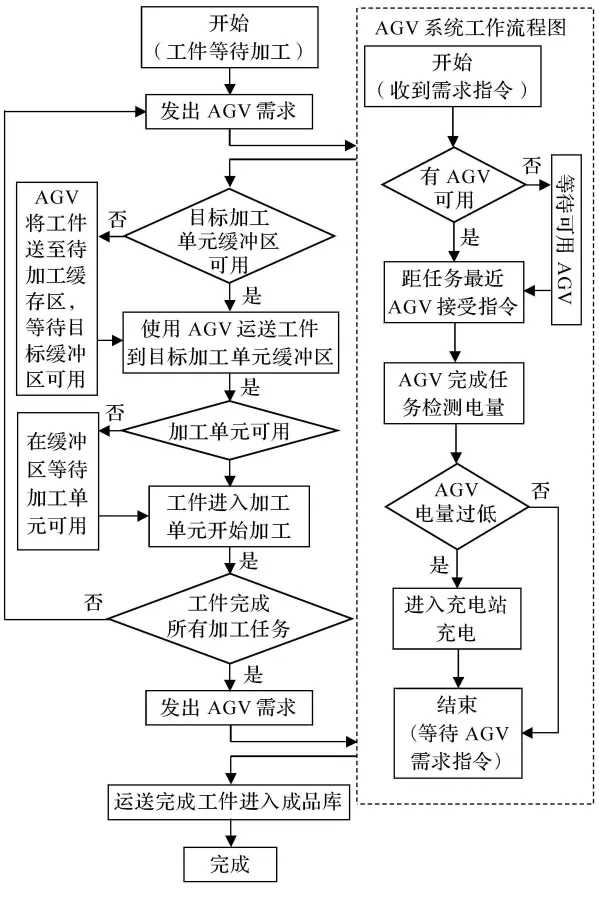
圖2 仿真流程圖

2.3 優化模型

對仿真結果進行方差分析是因為方差分析（ANOVA）是數理統計中常用的數據處理方法之一，方差分析就是根據試驗的結果進行分析，鑒別各個有關因素對試驗結果影響的有效方法，若隨機變量的取值集中在平均值附近，那么方差較小；若隨機變量的取值遠離平均值的分布，那么方差值就較大［7］.

在本文中只考慮車輛規模對于AGV系統響應時間的影響，因此為單因素試驗方差分析.主要的思路如下：原假設 H0∶μ1＝μ2，μ為平均響應時間，備擇假設H1∶μ1≠μ2，設車輛規模A有s個水平，在水平Aj（j＝1，2，…，s）下，進行nj次獨立的仿真實驗，在水平Aj下第i次仿真試驗的結果為Xij，則數據的總平均為則拒絕H0接受H1.

經過大量的仿真實驗以及文獻研究［2－3，8］，可以得到車輛數和平均響應時間有如圖3所示的關系，隨著車輛數的增加平均響應時間縮短，通過對相鄰的兩組實驗結果進行假設檢驗，可以得到拒絕原假設和接受假設的臨界點，在本研究中以AGV的平均響應時間為評價標準，認為該臨界點為所得到的車輛規模最優值.

3 系統運行流程

仿真優化系統的運行流程如圖4所示.

將估算模型，仿真模型，優化模型集成，建立整體模型.各個模塊通過軟件內部語言編輯程序進行集成，完成模塊間的通信、調用.

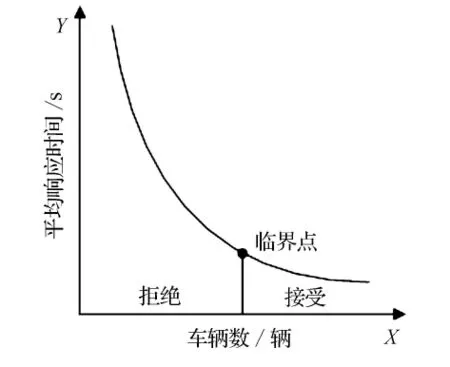
圖3 車輛規模與平均響應時間關系示意圖

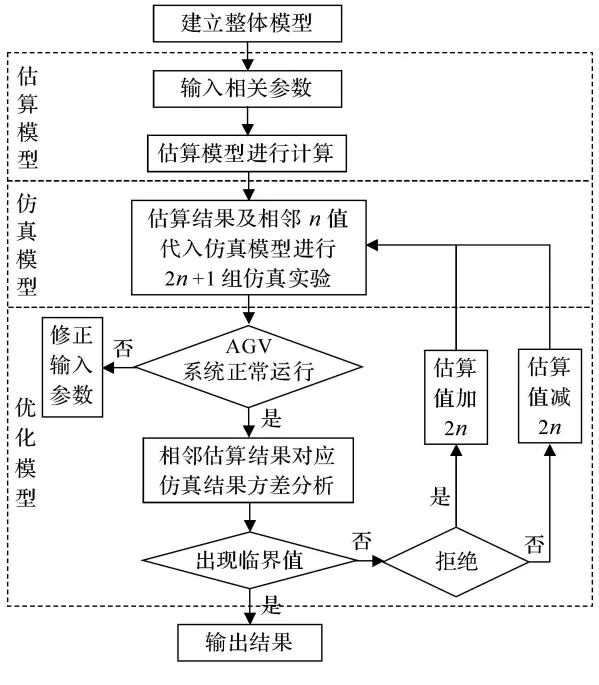
圖4 系統運行流程圖

4 實例分析

4.1 系統相關設置

本論文采用某研究院柔性制造系統為實例，驗證仿真優化方法確定AGV系統的車隊規模，該柔性制造系統由12個加工單元組成，立體倉庫有63個庫位，AGV車輛的設置為速度1m／s，加速度0.5m／s2.

為了簡化模型，在建模的過程中做出如下設置：（1）不考慮加工單元裝夾工件時間；（2）不考慮設備故障因素對仿真的影響；（3）忽略AGV系統的車輛堵塞；（4）AGV系統為單向行駛系統.

4.2 系統建模

采用Plant simulation作為系統建模平臺，該軟件具有面向對象和事件驅動的建模思想，層次化模型，強大的代碼擴展能力［9］等優點.基于以上優點建立柔性制造系統模型，同時使用軟件內部語言simtalk集成估算模塊，仿真模塊，優化模塊.如圖5所示，仿真界面由五部分組成，分別是立體庫區，AGV系統，生產制造單元，優化模塊，結果動態顯示區.

4.3 結果分析

表2～4顯示仿真優化過程得到最優解的過程.車輛數為3和4對應的仿真數據進行方差分析，結果如表2所列，F0.05（1，58）＝4.01＜13.47在顯著水平0.05下拒絕原假設H0，認為兩組實驗結果有顯著差異.車輛數為4和5對應的仿真數據進行方差分析，結果如表3所列，F0.05（1，58）＝4.01＞2.38在顯著水平0.05下接受原假設H0，認為兩組實驗結果無顯著差異.通過表4可以清楚地看出拒絕和接受原假設所對應的臨界值為4，因此在考慮平均響應時間單因素影響下車輛規模最優解為4輛.

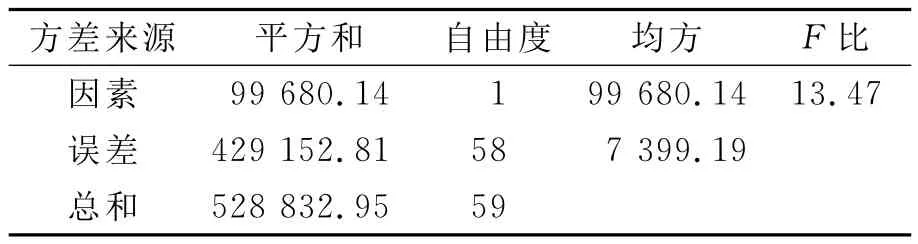
表2 車輛規模為3和4ANOVA結果

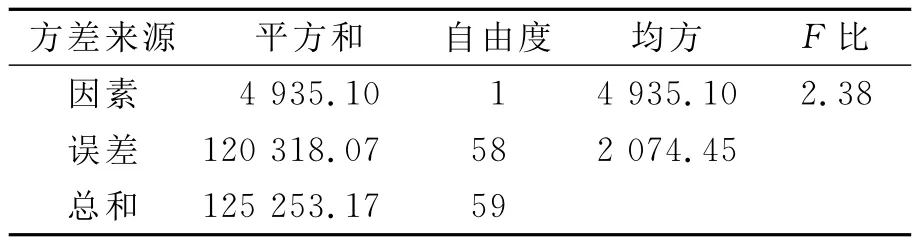
表3 車輛規模為4和5ANOVA結果

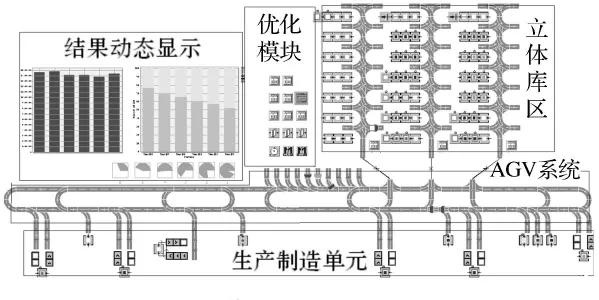
圖5 系統運行界面

為驗證仿真優化結果，選取AGV系統向某一加工單元運送工件的響應時間作為研究對象，如圖6所示為選取連續的30次運送行為，分別將AGV系統的車輛規模設置為2，3，4，5.由圖6可見，看到當車輛規模為2時，最大響應時間達到1 400s，嚴重影響系統的正常生產，車輛規模為3時平均響應時間明顯降低，但在第23次運送中出現最大響應時間600s，影響系統生產效率，車輛規模達到4時，從圖中可以看到可以滿足FMS系統的生產需要，并求得4輛AGV對應30次運送行為的響應時間對應以95%為置信度的置信區間為［135.64，170.37］，即有95%的概率平均響應時間在區間［135.64，170.37］內，當車輛規模繼續增加平均響應時間變化緩慢，考慮到AGV價格高昂，AGV系統成本將劇烈增加，從仿真實驗結果可以看出系統配置4輛AGV是比較理想的方案.

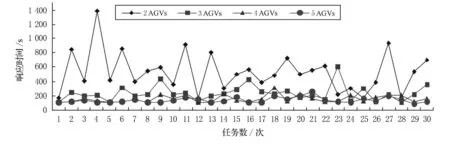
圖6 車輛規模與加工單元響應時間變化關系圖

5 結束語

本文研究了柔性制造環境下AGV系統車輛規模問題，采用仿真優化方法，通過計算機仿真軟件Plant Simulation建立優化模型，并通過估算的方法確定初始仿真實驗輸入變量取值范圍，提高了系統求解效率，節省了仿真成本.實例證明該優化方法能夠有效地獲得車輛規模的優化配置，并且計算效率較單純仿真實驗有顯著提高，同時彌補了解析方法求解誤差較大的缺點.

在研究的過程中沒有考慮不同車輛調度因素對車輛規模的影響，另外忽略了當車輛規模增大帶來的交通管理問題，這些方面可通過正交試驗設計，細化仿真模型等方法進一步研究.

［1］UM INSUP，CHEON Hyeonjae，LEE Hongchul.The simulation design and analysis of a flexible manufacturing system with automated guided vehicle system［J］.Journal of Manufacturing Systems，2009（28）：115－122.

［2］IRIS F A.Survey of research in the design and control of automated guided vehicle systems［J］.European Journal of Operational Research，2006，170：677－709.

［3］EGBELU P J.The use of non－simulation approaches in estimating vehicle requirements in an automated guided vehicle based transport system［J］.Material Flow，1987，4：17－32.

［4］MANTEL R J，LANDEWEERD.Design and operational control of an AGV system［J］.International Journal of Production Economics，1995，41：257－266.

［5］嚴武元.配送中心AGV配置方案仿真研究［J］.武漢理工大學學報：交通科學與工程版，2010（3）：635－638.

［6］王國新，寧汝新，王愛民.仿真優化在制造系統中的應用現狀及發展趨勢［J］.系統仿真學報，2008（1）：1－6.

［7］盛 驟，謝式千，潘承毅.概率論與數理統計［M］.北京：高等教育出版社，2002.

［8］VENTURA J A，RIEKSTS B Q.Optimal location of dwell points in single loop AGV system with time restrictions on vehicle availability［J］.European Journal of Operational Research，2009，192：93－104.

［9］林則孟.系統模擬理論與應用［M］.臺北：滄海書局，2006.