有關固體顆粒分散度與化學反應平衡常數關系的探討*

周宇行 王旭珍 靳長德

(1 大連理工大學化工與環境生命學部化工學院2008級 遼寧大連 116024；2 大連理工大學化工與環境生命學部化學學院 遼寧大連 116024)

在表面化學有關知識的習題中，有這樣一道題：“對于熱分解反應CaCO3(s)=CaO(s)+CO2(g), 在一定溫度下達到平衡，若保持其他條件不變的情況下，將CaCO3(s)由塊狀破碎為粉末狀時，分解壓如何變化？”

解答是：“CaCO3(s)粉碎后表面能增大，化學勢增高，平衡右移，K?變大，故分解壓(p(CO2))也變大”。

雖然讀者能夠理解答案所蘊含的道理，但對于這樣一個體系，從固體顆粒的大小(分散度、表面能)，關聯到平衡常數與分解壓，思維會有一些跳躍性。筆者意識到，這個例題應該是一個好題目，它提示我們：在化學熱力學部分重點討論過的通常只涉及無非體積功、雙變量系統的平衡常數表達式(即不考慮界面能貢獻的關系式)，當面對高度分散系統時，需要考慮分散度(或表面能)的影響，即需要將分散度作為變量,重新推導多組分多相反應系統平衡常數的表達式。在此，嘗試推導如下。

我們知道，對于化學反應，考慮相界面與不考慮相界面時,化學平衡判據的形式一致[1]，即：

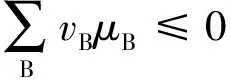
(1)

對于固態純物質和理想氣體的復相反應aA(s)+bB(g)=yY(s)+zZ(g)，各物質的化學勢表達式分別為：

其中，后兩個固體純物質的化學勢表達式推導如下：

對于純固體體相，化學勢只是溫度、壓力的函數[1-5]：

dμ=-SmdT+Vmdp

但對于高度分散系統，表面張力對固相產生的附加壓力不能忽略，故定溫下有：

這里認為p≈p?且固體不可壓縮。對于各向同性的固體，其附加壓力與液滴的類似(兩者區別可參考文獻[6])，即：Δp=σ(dAs/dV)；對于半徑為r的球體來說，dAs/dV=2/r，分散度aV=As/V=3/r，故：

將上述各物質的化學勢表達式代入式(1)，應用于球狀顆粒可得:

(2)

達到平衡時，∑vBμB=0，則有:

(3)

又由標準平衡常數的定義[2]:

即有:

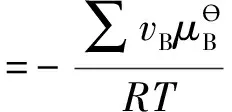
(4)

將式(3)兩邊同除以RT代入式(4),整理可得:

(5)

由式(5)可知，若不考慮分散度的影響，即aV,B=0，則有:

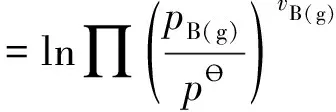
(6)

即K?=K′，顯然，式(6)與通常物理化學教材中化學平衡章節推導的平衡常數表達式完全一致。

若考慮分散度的影響，則有：

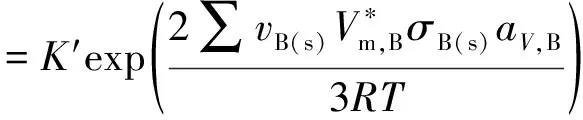
(7)

由此可以清楚地看出是否考慮分散度情況下表觀平衡常數K′的差別。

基于式(7)，結合前面的例題，假定在一定溫度下已達平衡的復相反應系統中產物CaO(s)顆粒的分散度不變，只考慮CaCO3(s)固體(v(CaCO3)=-1)由大顆粒粉碎為小顆粒并視為球體，由式(7)可知，此時分散度的改變對平衡常數的影響為：

(8)

因lnK?=f(T)，定溫下有定值，故有：

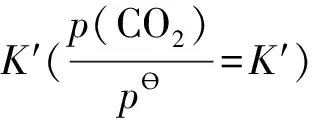
[1] 胡英.物理化學.第4版.北京:高等教育出版社,2005

[2] 傅玉普,王新平.物理化學簡明教程.第2版.大連:大連理工大學出版社,2007

[3] 王正烈,周亞平,李松林，等.物理化學.第4版.北京:高等教育出版社,2001

[4] 傅獻彩,沈文霞,姚天揚，等.物理化學.第5版.北京:高等教育出版社,2005

[5] 韓德剛,高執棣,高盤良.物理化學.北京:高等教育出版社,2001

[6] Cammarata R C.ProgSurSci,1994,46(1):1