基于混合遺傳算法的魯棒雙層規劃求解

李 硯，杜 綱，劉 波,2b

0 引言

魯棒優化是一種處理不確定參數優化問題的重要方法，由Soyster[1]于1973年首次提出，其區別于其它不確定優化方法的重要特征是模型對數據的不確定具有免疫性。由于魯棒優化對于不確定參數沒有假定分布，魯棒解被定為最壞不確定情景下使目標函數具有最優值的解。因此，魯棒優化規避了估計風險，同時也規避了低概率事件發生所帶來的巨大風險。魯棒優化的核心思想是將不確定性問題以一定的近似程度轉化為多項式時間內可以解決的確定性凸優化問題。

雙層規劃是具有主從遞階結構的層次優化問題，它將一個參數化的優化問題作為其約束條件[2]。在其層次決策框架中，下層決策者在上層決策者給定參數條件下優化自己的目標函數，而上層決策者基于下層決策者可能的最優反應來確定自己的決策參數以優化自己的目標函數，決策過程中上下層的決策與選擇行為相互依存。目前，雙層規劃模型在委托代理、供應鏈等諸多領域已經有著非常廣泛的應用。

本文將提出魯棒雙層規劃模型，針對目標函數和約束條件的系數均在橢球不確定集內擾動的情形，通過不等式約束處理將魯棒雙層規劃模型轉化為下層含有二階錐約束的非線性確定性問題進行求解，以此獲得魯棒解。對于含有二階錐約束(決策變量線性函數的二范數小于等于決策變量的線性函數)的規劃稱為二階錐規劃，它是對稱錐的特例，屬于非光滑凸規劃[3]。關于二階錐規劃的求解，具有代表性的算法主要有內點法、光滑牛頓算法、非內部連續化算法等。而雙層規劃的求解，即使是線性的，也是NP-hard的[4]。目前，雙層規劃的求解方法主要分為兩類：精確算法和智能算法。精確算法大多依賴于解空間的特性，無法解決一般的非線性規劃問題；智能算法具有較優的全局搜索能力，對目標函數要求較低，逐漸被用來解決雙層規劃問題。因此，本文擬提出一種混合遺傳算法求解魯棒雙層規劃模型轉化后的這類下層含有二階錐約束的確定性雙層規劃。

1 魯棒雙層規劃模型

1.1 問題描述

基于不確定雙層規劃中上下兩層的決策者均需獲得魯棒解的前提假設，考慮向量形式所表示的雙層規劃：

其中y解自于下面規劃問題：

其中，x∈Rm×1,y∈Rn×1,ci∈Rm×1,di∈Rn×1(i=1,2),A ∈ Rk×m,B ∈ Rk×n,h∈Rk×1。

假設式(1)的目標函數及約束條件的系數(c1,d1,c2,d2,A,B,h)均在橢球集合μ內擾動，記

其中，c?1,d1?,c2?,d2?,A?,B?,h?為給定的數據，A和A?的第i個行向量為aTi和(ai?)T，B和B?的第i個行向量為bTi和(bi?)T， 設 P01， P02∈ R(m+n)×(m+n), Pi∈R(m+n+1)×(m+n)為給定的尺度變換。

1.2 模型的轉化

系數在橢球集合μ內擾動的魯棒雙層規劃可以通過如下推導轉化成為系數確定的雙層規劃。

1.2.1 上層規劃問題的轉化

首先討論式(1)中上層規劃問題，其系數在橢球集合μ內擾動時，如何轉化為確定性問題。根據雙層規劃的庫恩—塔克條件法以及式(2)所表示的等價形式[5]

可得：

其中，Θ(d)={( x ,y,u,v)|Ax+by≥h,d2=BTu+v

當式(3)中的系數c1,d1∈μ時，利用文獻[5]中轉化形式：

其中c?是給定數據，P0是相應的尺度變換。

可以將不確定約束條件c1Tx+d1Ty≤t轉化為確定的約束條件

那么再次利用式(2)，得到

顯然，式(5)是式(6)用K-T條件法表示的等價形式:

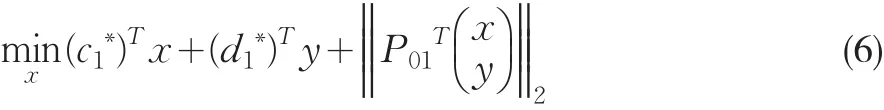
其中y解自于下面規劃問題：

從而就把系數不確定的上層規劃轉化為確定性規劃。

1.2.2 下層規劃問題的轉化

根據雙層規劃的決策框架以及上下兩層決策者均需獲得魯棒解的前提假設，一旦上層規劃給定決策變量x，那么下層規劃就是一個單層的魯棒規劃問題。同理，利用式(2)所表示的等價形式將下層目標函數轉化成約束條件，再通過式(4)的轉化形式對約束條件進行推導，則系數不確定的下層問題轉化為確定性問題。綜上，魯棒雙層規劃模型得以轉化為式(7)所表示的具有確定系數的雙層規劃問題：

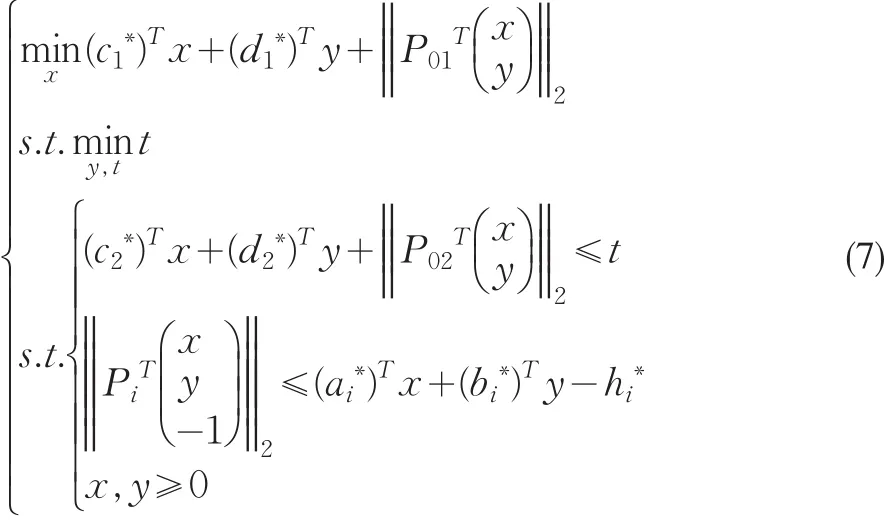
式(7)是下層含有二階錐約束的雙層規劃。

2 混合遺傳算法

上述魯棒雙層規劃模型，經過模型轉化得到了下層含有二階錐約束的確定性雙層規劃。本文提出一種混合遺傳算法求解這類轉化后的非線性雙層規劃問題。混合遺傳算法求解該問題的核心思想是：首先給出上層種群中個體x，通過改進的非內部連續化算法[6，7]求解下層的二階錐規劃,得到上層種群中每個個體x所對應的下層最優解y，進而由上層目標函數計算個體的適應度；然后對該群體進行選擇、交叉、變異等遺傳運算,通過上下層的反復迭代，逐漸逼近最優解。

2.1 非內部連續化算法

對下層二階錐規劃的求解，本文采用基于單個牛頓方程的非內部連續化算法[6]。非內部連續化方法的主要思想是：利用一個光滑函數把問題重新表述成一個參數化的光滑方程組，每步迭代利用牛頓法進行求解，通過令參數趨于零，期望得到原問題的一個解。該算法可以起始于任一點且不要求光滑路徑和迭代點位于正區域。文獻[6]提出了一個改進的求解對稱錐互補問題的非內部連續化算法。改進后算法的突出特點是在每步迭代中至多需要解一個線性方程組，并且在弱的條件下具有全局線性收斂性和局部二次收斂性，該算法被用來求解二階錐規劃。其中采用的二階錐光滑函數?μ為φμ(x,s):=φ(μ,x,s)=x+s-，其中μ∈R給定。

2.2 編碼和適應度函數設計

本文在遺傳算法中采用格雷碼對個體進行編碼，每個個體被遺傳到下一代種群中的概率是由該個體的適應度來確定的。在這里使用指數尺度變換的適應度分配方法。指數尺度變換時，新的適應度是原適應度的某個指數。指數尺度變換的公式為：

其中，系數β決定了選擇的強制性，β越小，原有適應度較高的個體的新適應度就與其他個體的新適應度相差較大，即增加了選擇個體的強制性。

2.3 操作算子策略

2.3.1 選擇算子

選擇算子采用兩種策略：一種是精華直接復制策略；還有一種是隨機遍歷抽樣策略。精華直接復制策略按適應度排列群體中的個體，采取最優保存策略復制適應度值最大的個體并使它直接進入下一代；而隨機遍歷抽樣策略將下一代個體中其余個體采用隨機遍歷抽樣方法產生，即：使用N個相等距離的指針，N是要求選擇的個數。種群被隨機排列在[ ]0,Sum/N范圍內產生一隨機數作為指針p tr，N個個體由相隔一個距離的N個指針[p tr,p tr+1,p tr+2,…,p tr+N-1]選擇，選取適應度范圍在指針位置的個體。另外，個體完全按它們在種群中的地位選擇，因此獲得最小的個體擴展和零偏差[8]。

2.3.2 交叉和變異算子

采用多點交叉策略。多點交叉有m個交叉位(當m=1時為單點交叉),ki∈{ }1,2,…,l-1是交叉點，l是染色體的長度，m個交叉位是通過隨機數選擇的，沒有重復、按升序排列。父母染色體中在兩個相連的交叉位間的基因進行交換，產生兩個新的子代。

設Pm為變異概率，產生一個[0,1]區間的隨機數r，如果r≤Pm，則對個體編碼串中以變異概率隨機指定某一位或某幾位基因位上的值做反轉變異運算(即0→1或1→0)或用其他等位基因值來代替，從而產生出新一代的個體。

2.4 算法過程

根據轉化后模型特點，結合上述討論，給出一種混合遺傳算法，整個算法的流程如圖1所示，具體步驟如下：

圖1 算法的流程圖

(1)隨機產生初始種群X,確定種群規模N以及交叉率Pc和變異率Pm,同時設定最大迭代數MAXGEN(終止條件)。

(2)對于上層初始種群X中的每個個體xi(i∈[1,N])代入下層二階錐規劃，利用改進的非內部連續化算法[6]求得上層種群X的每個個體xi所對應的下層規劃的最優解yi，上層目標函數作為適應度函數，再把X和Y代入到適應度函數，得到相應的適應度值。

(3)選擇算子操作，根據適應度函數值的大小對種群X的個體進行選擇,重復進行該過程,完成個體選擇過程。

(4)應用遺傳操作算子對選入下一代的個體進行交叉和變異算子操作，產生新的個體進入下一代。

(5)終止條件判斷(迭代次數大于最大迭代數)。如果條件滿足,則進化終止；否則,轉步驟(2)。

(6)輸出模型的最優解，算法運行結束。

3 數值算例

考慮如下魯棒雙層規劃問題：

其中y解自于下面規劃問題:

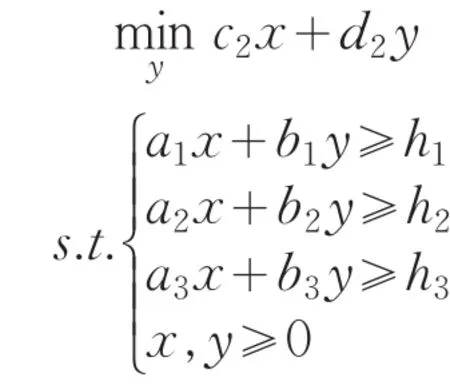
其中cl,dl(l=1,2);ai,bi,hi(i=1,2,3)

均屬于橢球擾動集μ，表示如下：

給定數據如下：

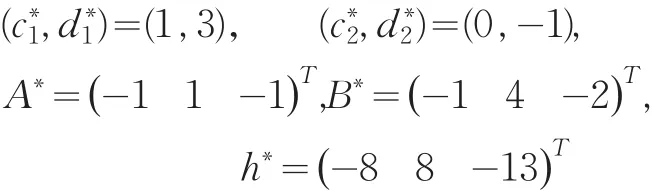
在區間[0,0.3]內隨機產生的尺度變換值如下：

利用2.2節中模型的轉化方法，并令z=(x y)T,得

其中y解自于下面規劃問題：

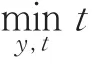
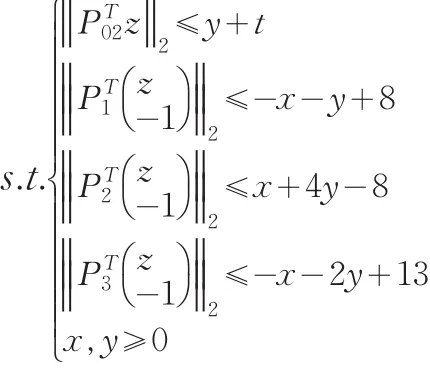
由上述算法步驟，通過MATLAB編程實現得到上層決策變量的魯棒解為:x=6;上層目標函數的最優值為:Fmin=12.7294;下層決策變量的魯棒解為：y=1.6139;下層目標函數的最優值為：fmin=0.4918.

當假設所有尺度變化均為零，即參數處于名義值時，問題本身為確定的線性雙層問題，即文獻[2]的算例。利用該算法得到上層決策變量的最優解為:x=6;上層目標函數的最優值為:Fmin=12;下層決策變量的最優解為:x=2;下層目標函數的最優值為:fmin=-2。與算例同解。

4 結語

本文基于上下兩層決策者均需獲得魯棒解的前提假設提出了系數不確定雙層規劃的魯棒問題，采用不等式約束處理將原問題轉換為下層是二階錐規劃的確定性雙層規劃問題。根據轉化后模型特點，設計了相應的混合遺傳算法，并且由于常值函數、線性函數、歐氏范數、P范數函數及偶冪函數都具有二階錐集性質，可以將含有這些函數的規劃轉化為二階錐規劃進行求解[5]。因此，該算法不僅能獲得高質量的全局最優解，而且本身具有通用性，可以求解更一般的雙層規劃問題。本文通過算例驗證了算法的有效性及可行性。

[1]Soyster A L.Convex Programming with Set-inclusive Constraints and Applications to Inexact Linear Programming[J].Operations Research,1973,(21).

[2]Dempe S.Foundations of Bilevel Programming[M].Boston:Kluwer Academic Publisher,2002.

[3]Alizadeh F,Goldfarb D.Second-order Cone Programming[J].Mathe?matical Programming,2003,95(1).

[4]Jeroslow R.The Polynomial Hierarchy and a Simple Model for Com?petitive Analysis[J].Mathematical Programming,1985,32.

[5]Lobo M S,Vandenberghe L,Boyd S,etc.Applications of Second-order Cone Programming[J].Linear Algebraand its Applications,1998,284(1).

[6]Lu N,Huang Z H.Convergence of a Non-interior Continuation Algo?rithmfor the Monotone SCCP[J].Acta Math.Appl.Sinica(English Se?ries),2010,(4).

[7]Huang Z H.The Global Linear and Local Quadratic Convergence of a Non-interior Continuation Algorithm for the LCP[J].IMA Journal of Numerical Analysis,2005,(25).

[8]雷英杰,張善文,李續武等.MATLAB遺傳算法工具箱及應用[M].西安:西安電子科技大學出版社,2005.