基于地貌指數的汶川地震災區單溝泥石流總量計算方法*

張懷珍，范建容

(1.中國科學院山地災害與地表過程重點實驗室，四川成都610041;2．中國科學院·水利部成都山地災害與環境研究所，四川成都610041;3.中國科學院研究生院，北京100049)

基于地貌指數的汶川地震災區單溝泥石流總量計算方法*

張懷珍1，2，3，范建容1，2

(1.中國科學院山地災害與地表過程重點實驗室，四川成都610041;2．中國科學院·水利部成都山地災害與環境研究所，四川成都610041;3.中國科學院研究生院，北京100049)

現行的泥石流總量計算方法普遍存在計算參數較難獲取或難以精確獲取的問題，加上汶川地震災區溝谷內分布大量的由崩塌、滑坡體等形成的固體松散物質;所以多數泥石流總量計算公式在汶川震區存在局限性。參考適用于以崩塌、滑坡體為主要物源的泥石流總量計算公式;分析研究區范圍內地形地貌發育狀態與降雨因素及其地質條件之間的影響關系;將地貌指數(Strahler積分)應用于泥石流總量計算，嘗試解決缺乏降雨數據情況下泥石流總量計算問題。根據“8.13”四川清平群發性泥石流數據初步回歸分析得到適合于汶川震區的泥石流總量計算模型。

單溝泥石流總量;汶川地震災區;地貌指數;降雨

泥石流的形成過程十分復雜，其受地質、地形地貌及降雨條件等因素影響。在泥石流研究中，泥石流總量(一次泥石流事件中泥沙流出量)的確定既是泥石流危險性評價的關鍵參數，也是整個泥石流學科研究的重點。泥石流總量也是泥石流危險區面積、堆積長度、堆積厚度、最大流量等參數計算過程的中間參數。泥石流總量受到地質、地形、土壤、土地利用方式及降雨等泥石流形成因素的影響［1］。目前，關于泥石流總量的研究很多，多為建立在水文計算、調查和統計分析基礎上的間接確定方法和經驗、半經驗公式;如雨洪修正法、泥痕調查法和配方法等。但由于多數公式存在參數較難獲取或難以精確獲取的問題;加上不同區域泥石流溝谷的區域性差異，使得這些公式難以推廣［1－3］。最近，Gartner，J.E.，Cannon，S.H. 等通過對美國西部受火燒擾動區域的泥石流進行分析，經回歸統計分析建立了適合于受火燒影響區域的泥石流總量計算模型［2－3］。莊建琦、崔鵬等(2009)參考受火燒影響的區域中泥石流總量的計算公式，結合受地震影響嚴重的云南蔣家溝泥石流實測數據，建立了受地震影響以崩塌、滑坡體為主要物源的泥石流總量計算模型［4］。

汶川大地震在岷江干流及其支溝兩岸山坡引發了大量崩塌、滑坡，形成大量的松散固體物質，這些松散固體物質為泥石流形成提供直接物源，使得泥石流活動性增強［5－7］。本研究參考適合于以崩塌、滑坡體為主要物源的泥石流總量計算公式，分析研究區范圍內地貌指數與降雨因素及其地質條件之間的影響關系，將地形地貌定量指數(Strahler積分)引入汶川震區泥石流總量計算，為震區災后重建的工程措施設計建設提供參考數據。

1 研究區概況

研究區位于汶川地震主災區，主要包括沿龍門山斷裂帶區域的白龍江上游、岷江上游、青衣江上游及部分小流域，經緯度范圍處于102.5°～106.5 °E，29.2°～34.4°N(圖 1)。該區域主要位于四川西部山區，山高谷深，地質構造復雜，斷裂發育，屬于滑坡和泥石流等山地災害多發區。強烈地震導致山地區域的地質環境更加脆弱，整個震區滑坡、泥石流活動更加頻繁、危害更加嚴重［5－7］。

地震形成的大量崩塌、滑坡直接為泥石流活動提供了豐富的松散固體物質，且地震造成大量坡體失穩和巖體破壞;使這些泥石流溝在今后較長一段時間內處于活躍期，泥石流暴發規模和頻率顯著增加［5－6］。崔鵬等指出震后次生災害將進入活躍期，崩塌、滑坡的活躍期可能持續5～10年，泥石流的活躍期將可能持續20年。在未來5～10年內，因滑坡、泥石流強烈活動，災害鏈［崩塌、滑坡→(泥石流→)堰塞湖→潰決洪水或泥石流］表現比較突出;隨著泥石流、滑坡活動強度降低，災害鏈表現逐漸減弱，出現概率減小［5］。

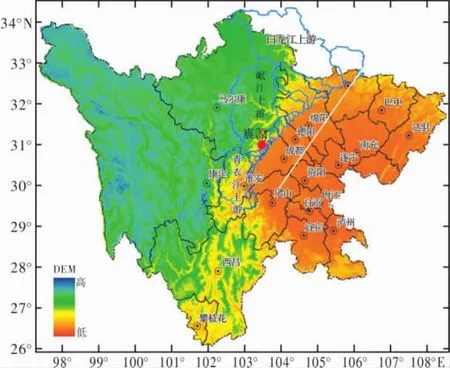
圖1 研究區位置示意圖

2 研究方法

目前，多數泥石流總量計算公式存在參數獲取困難或參數缺乏準確性問題;而且現行的泥石流總量計算公式對于汶川地震形成的后發型地震泥石流存在一定的局限性。關于汶川震區泥石流總量計算的研究較少。莊建琦等參考受火燒影響區域的泥石流總量計算公式［2］:

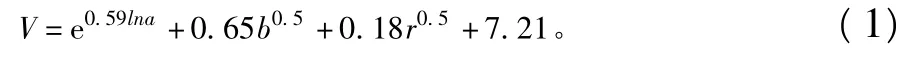
式中:V為泥石流總量(m3);a為坡度大于30%所占面積(km2);b為中度以上被火擾動的落地面積(km2);r為降雨量(mm)。結合云南蔣家溝實測泥石流數據得到受地震影響以崩塌、滑坡體為主要物源的泥石流總量V1計算公式［4］:

式中:V為泥石流總量(m);A為坡度大于30%所占面積;B為崩塌、滑坡體所占面積(km2);R為年最大日降雨量(mm)。這三個基本參數可理解為是對泥石流形成所需三個基本條件的描述參數:地形地貌條件(A)、物源補給條件(B)和降雨激發條件(R)。但在公式(2)中，R年最大日降雨量的獲取較困難，給缺乏降雨數據情況下的泥石流總量計算帶來一定的困難。

2.1 地貌發育狀態與降雨因素之間的關系研究

降雨是重要的外營力作用之一，降雨因素在一定程度上影響地形地貌的發育。本研究從地形地貌發育條件出發，選擇能夠定量化描述地形地貌發育狀態的地貌指數Strahler積分，研究其在所選研究區范圍內與降雨因素的關系。Strahler積分是由美國地貌學家A.N.Strahler提出的面積－高程分析法計算獲得，用來定量分析地貌發育階段［8－9］。

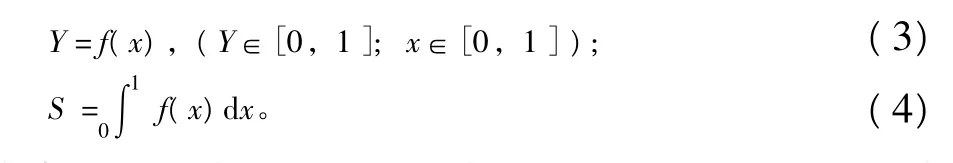
式中:Y=h/H，x=s/A;s，h分別為流域內某一點以上的流域面積和到流域最低點之間的高差;H，A分別為流域的最大高差和流域面積;S為斯特拉勒(Strahler)積分，其大小流域地貌發育有關，能夠用來量化戴維斯模型的侵蝕流域地貌演化階段［8－9］。

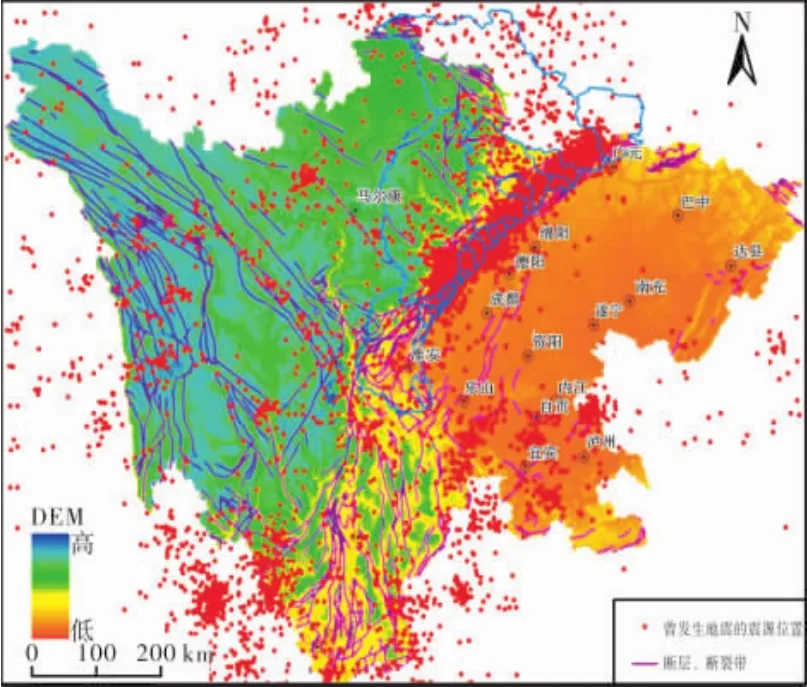
圖2 研究區地質數據及地震數據

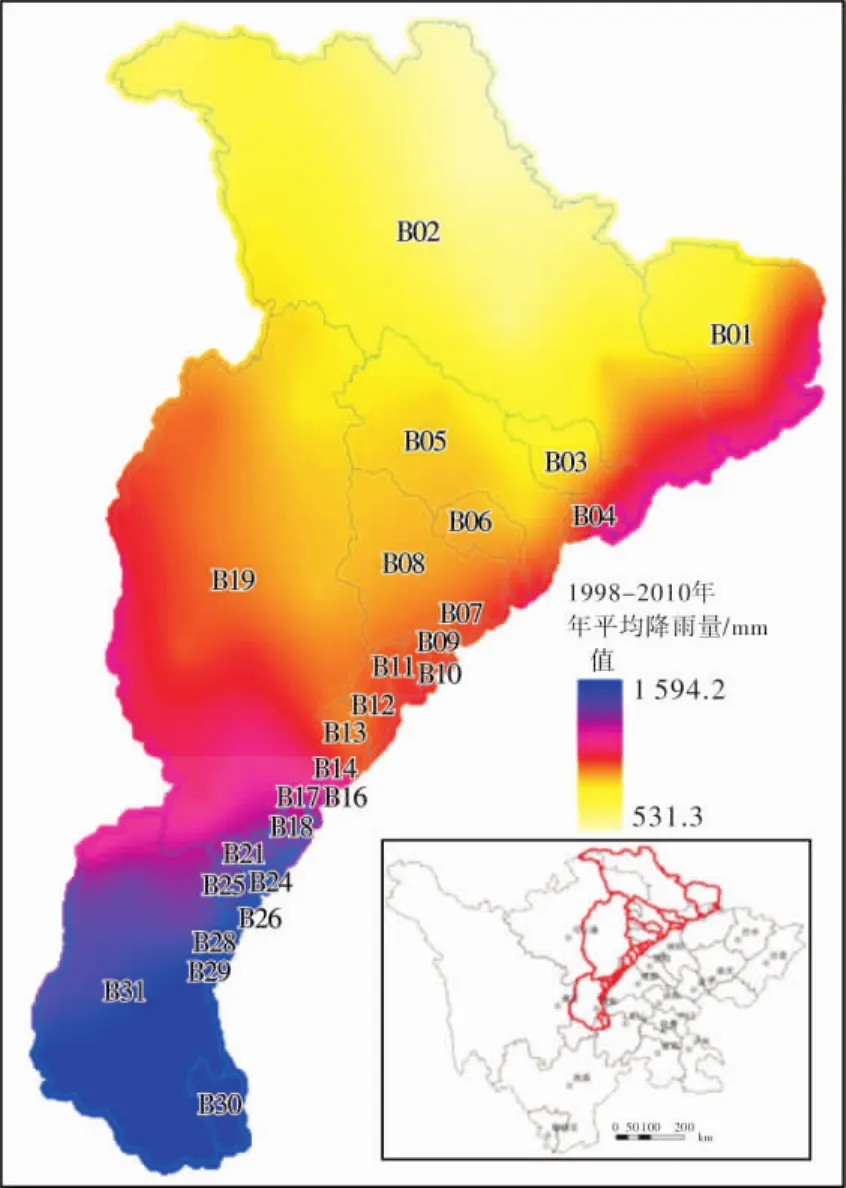
圖3 研究區多年平均降雨量

研究區沿龍門山斷裂帶分布，地質構造復雜，斷裂發育，地質活動(地震)頻繁(圖2)。整體上看，研究區是地震活動強烈和地震災害嚴重的區域。即研究區范圍內影響地貌發育的內營力作用分布差別不大。參考研究區多年平均降雨分布(圖3)，研究區多年平均降雨量基本上從東南向西北方逐步減少。即研究區不同區域降雨量存在一定的差異。因此，在內營力差別不大的情況下，外營力(降雨)的差別將會是影響研究區地形地貌發育的重要因素。

首先利用ArcGIS9.2的水文分析模塊將研究區劃分為31個流域，經統計分析計算獲得每個流域研究單元內的多年平均降雨量的平均值Rs，將其作為降雨因素的一種定量指標;然后以DEM為基礎，經統計分析計算獲取每小流域研究單元的Strahler積分S(表1)。

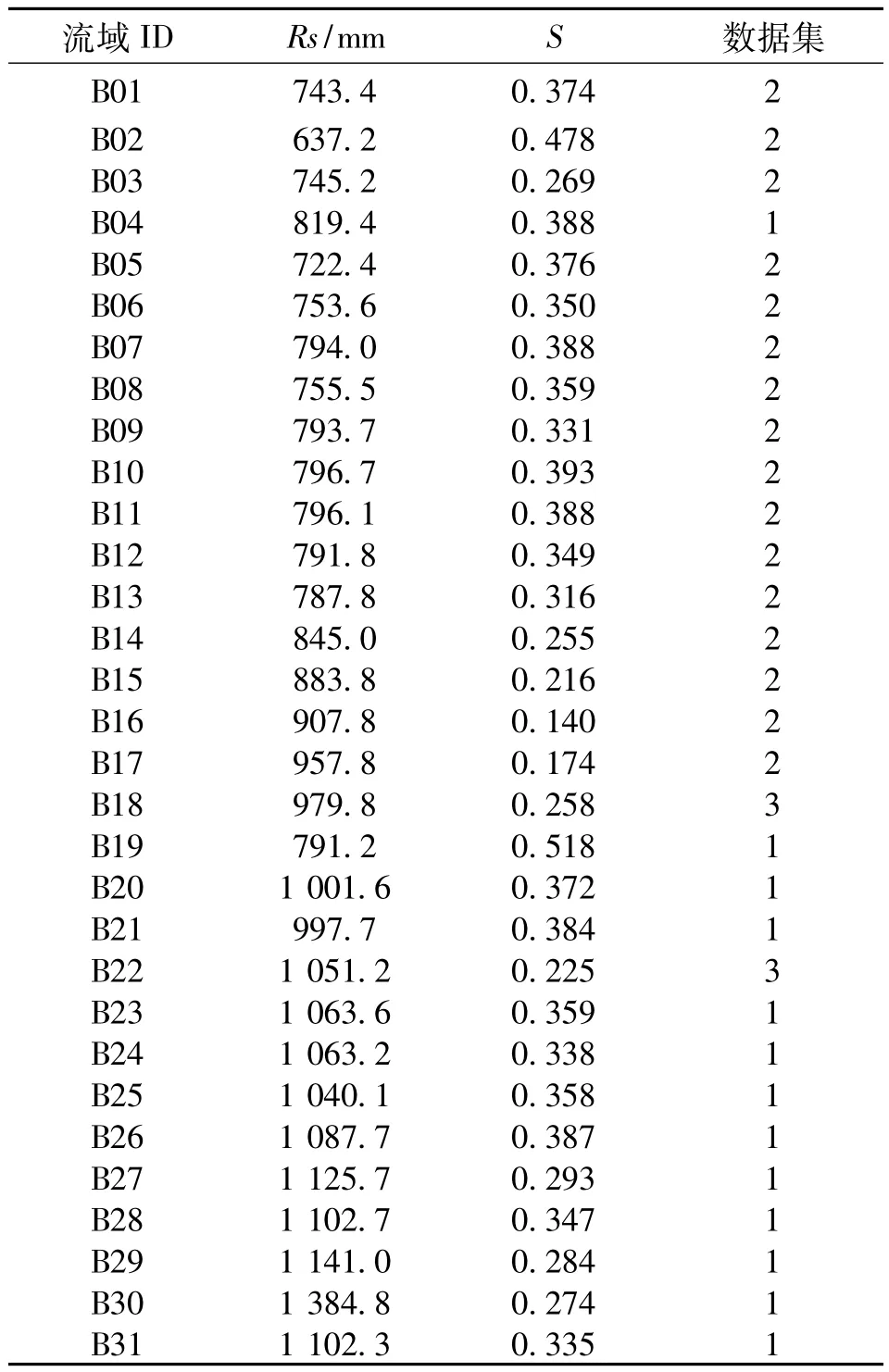
表1 研究區流域研究單元基本數據

對研究區的Rs和S數據進行聚類分析，將研究區數據分為3個數據集(表1)。整體上，研究區小流域的S與Rs存在兩種主要關系。數據集1存在函數關系:

數據集2存在的函數關系:

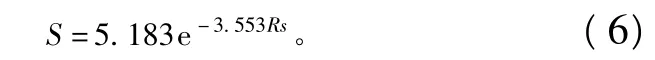
數據3由于數據量有限未做分析。數據1，2和3的整體分布趨勢如圖4所示。

通過上述分析，地貌指數Strahler積分S與降雨因素存在一定的函數關系。在不同區域受地質條件的影響，不同區域的地貌指數Strahler積分S與不同降雨因素的定量指標存在不同的函數關系。但多年平均降雨量只是降雨因素的一種。

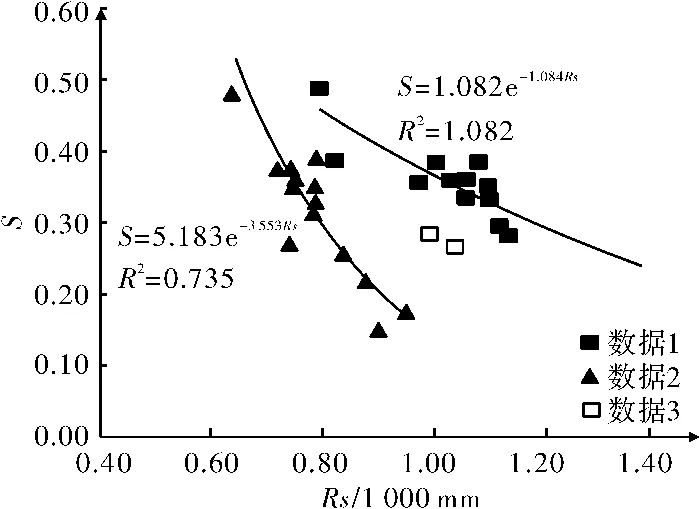
圖4 研究區小流域的S與Rs關系圖

為進一步研究地貌發育狀態與降雨因素之間的影響關系。選擇研究區內岷江上游24條小流域(表2);研究分析地貌指數與降雨因素R(年日最大降雨量)之間的關系。研究結果表明，該區域內的小流域地貌指數S與降雨因素R的存在一定的函數關系(圖5):

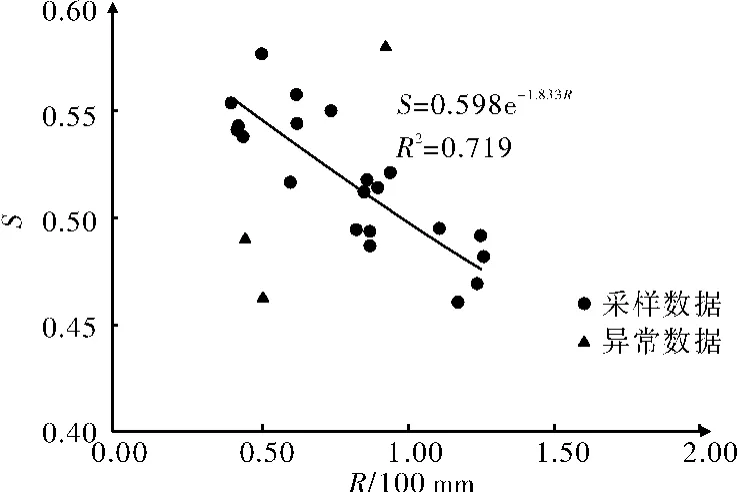
圖5 岷江上游小流域的S與R關系圖

綜上所述，地貌發育狀態與降雨因素存在一定關系。在大流域范圍內，Strahler積分S與年降雨量Rs存在一定函數關系;在小流域(泥石流單溝)范圍內，Strahler積分S與年日最大降雨降雨量R存在一定關系。

2.2 引入地貌指數的泥石流總量計算方法

地貌是內外營力相互作用的結果;地貌狀態是對內外營力相互作用的外在體現。地貌指數Strahler積分S是面積與高程的函數積分，是對地表形態的定量化參數;地質條件會影響地貌發育的快慢程度;加上地貌指數S與區域的降雨因素存在關系。因此，地貌指數Strahler積分S包括地形、地質條件和降雨因素三方面的信息。

公式(1)和(2)考慮地形、物源補給及降雨三方面因素，由于地貌指數S包括地形、地質條件和降雨因素方面的信息;因此，引入地貌指數S時公式(2)和(9)中的參數ln A、B0.5的系數都會改變。結合岷江上游24條泥石流溝小流域基本數據，對公式(1)和公式(2)進行改進:

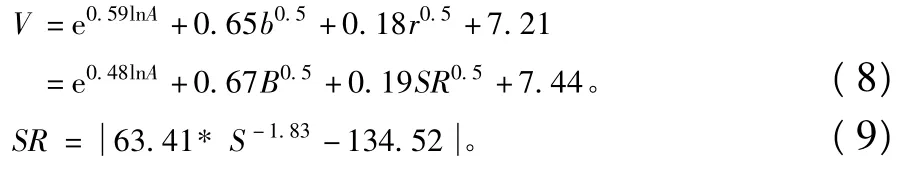
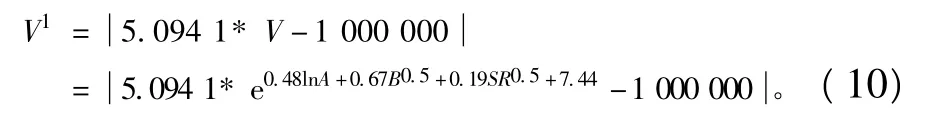
由公式(2)和公式(10)計算出24條泥石流溝的泥石流總量V2、V9(表2):V2、V9兩者的相關系數(Person系數)達到0.868，除去離群值后Person系數高達0.932。

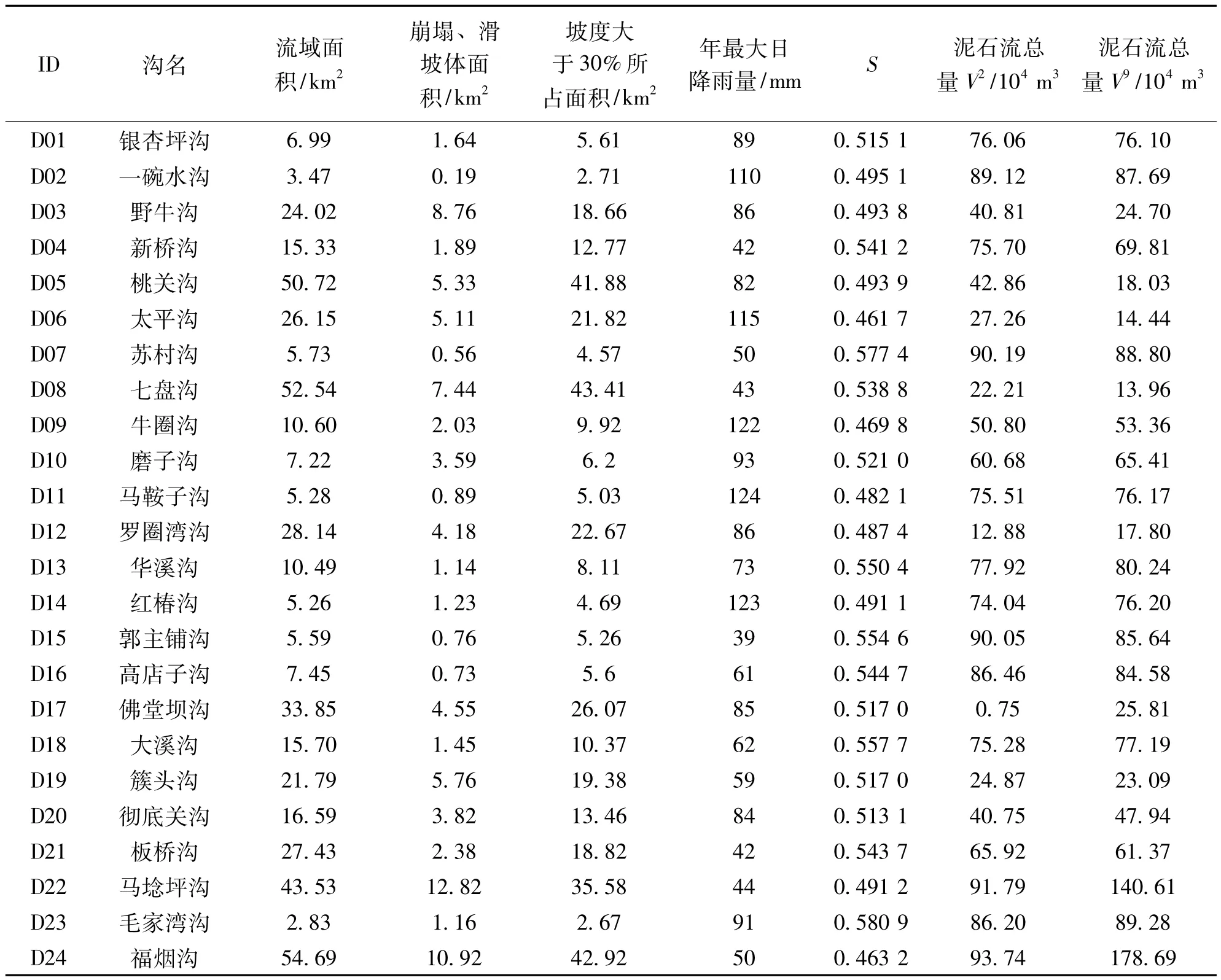
表2 岷江上游泥石流溝基本參數及其泥石流總量計算值［4］

綜上所述，在缺乏降雨數據的情況下，在一定區域內用地貌指數S計算泥石流總量能夠取得較理想的結果，能夠解決缺乏降雨數據情況下的泥石流總量計算問題。

3 實例分析研究

清平鄉地處四川省綿竹市西北部山區的綿遠河上游，屬沱江正源。該區域在汶川地震中形成大量的崩塌、滑坡體，導致該區域的泥石流活動頻發，災害更加嚴重。

2010年08月12 －13日和18－19日在兩次區域強暴雨作用下，該區域暴發了大規模、群發性泥石流災害。由于該區域泥石流物源主要是由地震誘發的崩塌、滑坡體形成的固體松散物質，故適合于公式(9)計算泥石流總量。

根據綿遠河上游泥石流溝的基本參數按照公式(9)進行計算，得到泥石流總量的計算結果(表3)。對比“8.13”群發性泥石流事件中各泥石流溝沖出固體松散物質總量M與公式(9)的計算結果;對于本次泥石流事件中沖出固體松散物質總量M小于10×105m3泥石流溝的計算泥石流總量V1明顯偏大;但對于規模大于100×105m3的泥石流計算結果偏小。為便于分析分析原因，按照公式(8)計算泥石流總量V(表3)。同樣對比V與M;在M小于10×105m3的情況下，V在多數情況下相比V1接近M;但在M大于10×105m3的情況下，V明顯偏小。因此，直接以云南蔣家溝數據為基礎計算出的適合于受地震影響以崩塌、滑坡體為主要物源的泥石流總量計算公式(2)在研究區域的“8.13”群發性泥石流事件適用性上存在一定局限性。

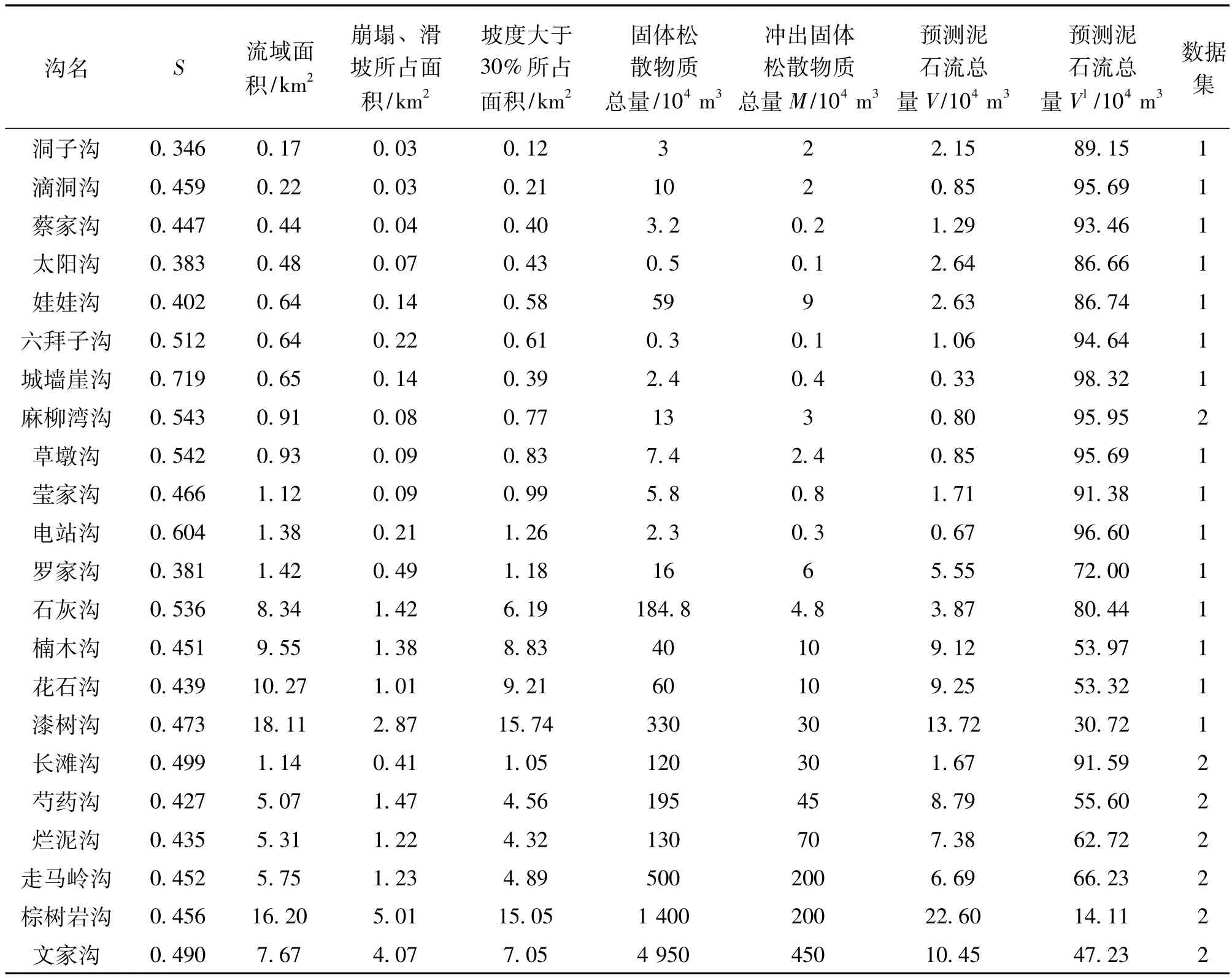
表3 綿遠河上游泥石流溝基本參數及泥石流總量計算值［10］

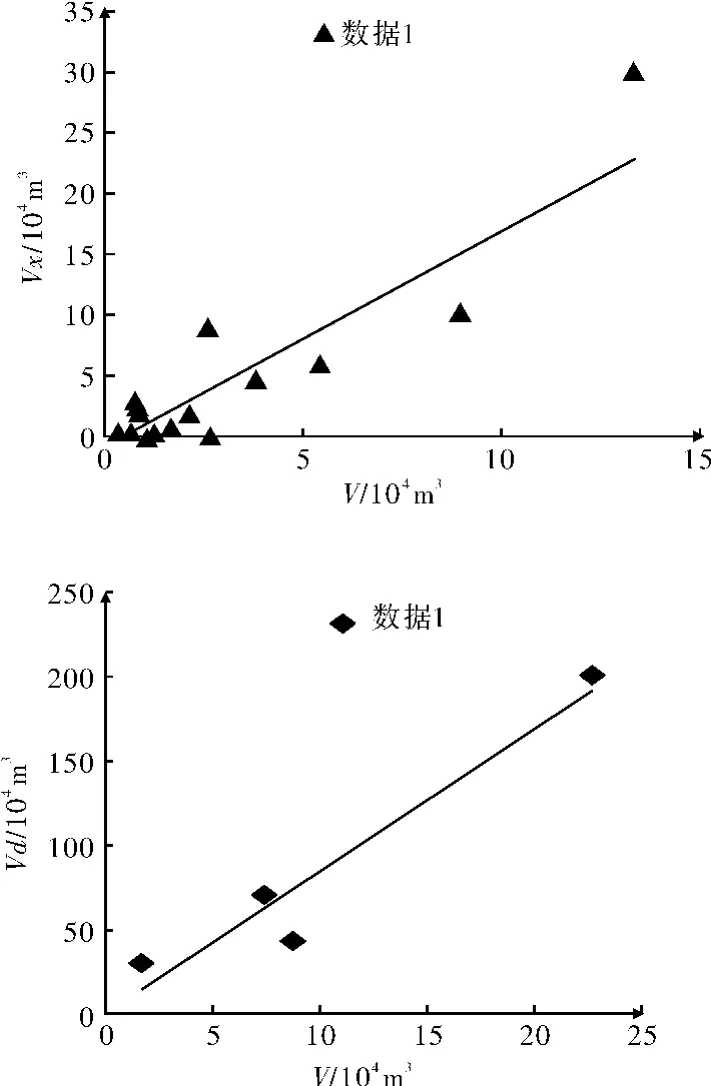
圖6 泥石流總量Vx，Vd與V之間的關系

由于公式(2)是以公式(1)為基礎，參考云南蔣家溝數據改進獲得。但云南蔣家溝的泥石流形成條件與汶川震區存在一定的差異;因此公式(2)計算得到泥石流總量在汶川震區存在差異，即公式(2)在汶川震區存在適用性局限性。為研究適合于汶川震區的泥石流總量計算方法;對“8.13”泥石流事件中泥石流的基本數據進行分類，將研究區數據分為兩類(表3)。提出部分離群值后，對于數據1(Vx)和數據2(Vd)與公式(8)計算結果V存在函數關系:

式中:Vx、Vd和 V的單位是104m3。由于公式(11)是根據區域泥石流計算獲得，且數據量有限;其在其他區域的適用性有待進一步驗證。

通過本實例得到初步結論:適合于受地震影響以崩塌、滑坡體為主要物源的泥石流總量計算公式(2)是區域性經驗公式。但公式(2)對受火燒影響區域的泥石流總量計算公式(1)的改進很成功。在不同區域，泥石流總量與公式(1)的計算結果可能存在不同的函數關系;因此在實際運用中應該參考臨近區域泥石流數據確定泥石流總量與公式(1)計算結果的函數關系;但對于部分泥石流仍較難計算。

4 結論

地貌發育狀態是內外營力相互作用的結果;地貌指數能夠體現影響地貌的內外營力的多方面信息，包括地質構造、降雨等方面的信息。本研究將地貌指數Strahler積分S用于泥石流總量的計算;嘗試解決缺乏降雨數據情況下泥石流總量計算問題。但由于不同區域形成泥石流的條件存在差異，泥石流總量計算較難形成統一的計算公式。根據“8.13”清平群發性泥石流數據對泥石流總量計算公式進一步改進，初步得到該區域的泥石流總量計算模型。

總體上，適合于受地震影響以崩塌、滑坡體為主要物源的泥石流總量計算公式(2)在汶川地震災區存在局限性;對于汶川震區泥石流總量的計算方法還需要根據該區域的泥石流實測數據進行改進完善。本研究根據綿遠河泥石流實測數據對公式(1)進行了初步改進，并得到該區域泥石流總量初步計算公式;其計算結果具有一定的參考價值;但需要根據更多的數據進行改進和完善。

［1］Rickenmann D．Empirical relationships for debris flows［J］．Natural Hazards，1999，19:47 －77．

［2］Gartner JE，Cannon SH，Santi PM，etal．Empiricalmodels to predict the volumes of debris flows generated by recently burned basins in the western U．S．［J］．Geomorphology，2008，96:339－354．

［3］Cannon S H，Gartner，JE，Rupert M G，et al．Predicting the probability and volume of postwildfire debris flows in the intermountain western United States［J］．Geological Society of America Bulletin，2010，122(1/2):127－144．

［4］莊建奇，崔鵬，葛永剛，等．“5·12”地震后都汶公路沿線泥石流溝危險性評價［J］．四川大學學報:工程科學版，2009，41(3):131－139．

［5］崔鵬，韋方強，陳曉清，等．汶川地震次生山地災害及其減災對策［J］．中國科學院院刊，2008，23(4):317－323．

［6］謝洪，鐘敦倫，矯震，等．2008年汶川地震災區的泥石流［J］．山地學報，2009，27(4):501－509．

［7］崔鵬，韋方強，何思明，等．“5·12”汶川地震誘發的山地災害及其減災措施［J］．山地學報，208，26(3):280－282．

［8］艾南山．侵蝕流域系統的信息熵［J］．水土保持學報，1987，1(2):1－8．

［9］艾南山，岳天祥．再論侵蝕流域系統的信息熵［J］．水土保持學報，1988，2(4):1－9．

［10］蘇鵬程，韋方強，馮漢中，等．“8·13”四川清平群發性泥石流災害成因及其影響［J］．山地學報，2011，29(3):337－347．

Method of Calculating Single Gully Debris-flow Volume in W enchuan Earthquake Area Based on M orphometric Index

Zhang Huaizhen1，2，3and Fan Jianrong1
(1．Key Laboratory of Mountain Hazards and Surface Process，Chengdu Institute of Mountain Hazards and Environment，CAS Sciences，Chengdu 610041，China;2．Institute of Mountain Hazards and Environment，CAS＆ Water Resources，Chengdu 610041，China;3．Graduate University of the Chinese Academy of Sciences，Beijing 100049，China)

Most available equations for estimating amaximum debris-flow volume have the limitation in requiring uncertain input parameters．In addition，landslips and landslides that occurred in the debris-flow source area of the Wenchuan earthquake zone contributed extensively to the debris-flow volume．Most equations have the limitation in this area．This study is based on an equation that is fit for debris-flow in earthquake zone．The relationships among morphometric condition，rain and other geological conditions are analyzed．The morphometric index(Strahler Integration)is tentatively used to calculate debris-flow volume when rain condition data are unavailable．A model suitable for calculation of debris-flow volume ofWenchuan earthquake zone isworked out based on regression analysis of the data of group debris-flows in Qingping Town，Mianyuan River Upstream，Sichuan．

single debris-flow volume;Wenchuan earthquake zone;Morphometric Index;rain

P642.23

A

1000－811X(2012)03－0086－06

2011－11－22

2012－02－06

國家科技支撐計劃課題(2011BAK12B03)

張懷珍(1985－)，男，山東東昌府區人，碩士研究生，主要研究方向為環境遙感與GIS應用．E-mail:zhz198508@163.com

范建容(1969－)，女，四川井研縣人，博士，研究員，主要研究方向為環境遙感與水土保持．E-mail:fjrong@imde.ac.cn