閉環控制系統串聯校正裝置參數的調試

何明睿

HE Ming-rui

(山東工業職業學院，淄博 256414)

0 引言

隨著自動控制在設備中的廣泛應用，為使系統具有好的動、靜態指標，校正裝置參數的確定成為當前設計和調試自控設備的重要技術問題。本人過去采用試探法，既麻煩又不準確。所謂試探法，就是通過試探改變校正裝置的參數，觀察響應曲線，當覺得曲線比較好時就算調試完畢。例如：下面的比例積分校正環節，只知道增大減小C1就可以改變系統的開環放大倍數和微分環節，增大減小R1就可以改變微分環節的大小，從而影響系統的特性。但并不確定C1、R1該多大最好，只有通過多次試探才能得到比較好的特性。后來經過多次實踐，總結出一個適合PI調節器的既快又準確的調試方法，能使系統在力所能及的情況下，既反應快又穩定。得到最佳的動態性能，下面說明之。

1 固有系統數學模型的估計

固有部分數學模型的求取需要精確的測量。要確定準確的數學模型是很困難的，甚至是不可能的。例如電動機的機械慣性多大、晶閘管整流裝置的慣性多大都不好確定。但根據系統的構成，確定系統有幾個慣性環節，慣性的大小大概是多大，還是容易估算的。這樣，在不知道系統準確參數的情況下，通過一定的步驟，調試出系統的最佳性能就成為自動控制界最適用的技術。例如：我院的直流調速實驗系統固有部分的結構圖是由直流電機的機械慣性環節（T1S+1）和直流電機電磁慣性與晶閘管整流裝置慣性兩個慣性合成的等效慣性（T2S+1）組成, （T1S+1）屬于機械慣性比較大，（T2S+1）屬于電磁慣性比較小。整個系統的結構圖如圖1(a)所示。其中，Wc(S)是串聯校正裝置，采用PI調節器，其連接圖如下圖1（b）所示。

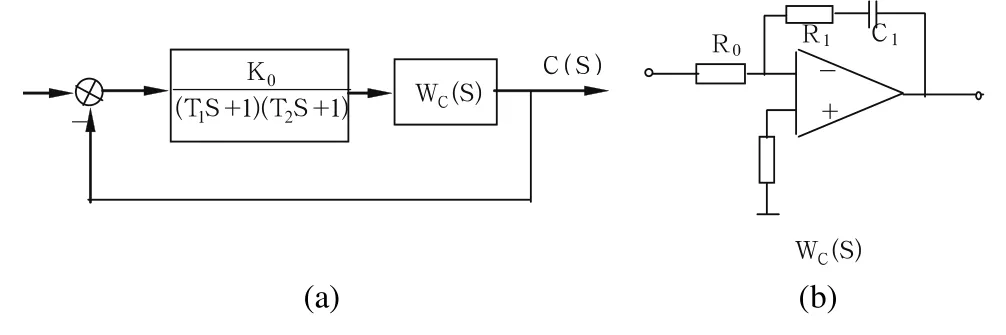
圖1 系統結構圖及校正裝置

2 調試過程的理論根據

在自控系統的分析中，頻率法是簡單方便的。下面在頻率特性分析的基礎上，總結出調試的步驟。

先讓串聯校正裝置的傳遞函數Wc(S)＝ 可見該校正裝置是積分校正環節，如圖1(b)所示，R1=0。可推得τ=R0C1。

加積分環節串聯校正后，系統的頻率特性可能是圖2所示的三種情況之一。

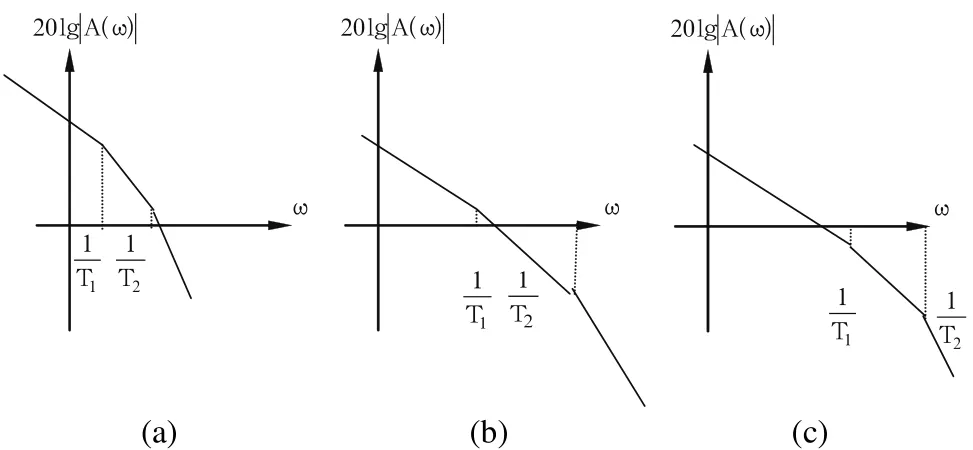
圖2 系統積分校正的波德圖

其中τ＝R0C1，如圖中電路所示，整個系統的開環放大倍數 ：

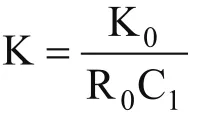
可見， 增大C1(R0不能變)會使系統的放大系數減小，頻率特性下移。根據奈氏判據，若系統為圖2(a)、(b)所示的頻率特性，系統則可能發生振蕩。當C1大到圖2(c)所示的特性時，系統就絕不會振蕩了，但快速性變差。為了增加快速性，可逐漸減小電容C1，使頻率特性上移，直到系統出現輕微振蕩，此時的頻率特性應當是圖2（b）所示，然后增大R1，這時，調節器變成比例－積分調節器 ，如圖1（b）所示。其傳遞函數為：

根據工程設計零極點抵消的辦法，若選τ=T1，則傳遞函數變為：是典型的二階系統，當K選得合適，其頻率特性如圖3所示，既快又不振蕩，動態性能好。由上式可見，變R1時，系統的放大倍數K是不變的，只能改變微分環節的時間常數τ＝R1C1。而改變C1時，不但能改變τ，而且能改變系統的放大倍數K。據此來調節τ＝R1C1的大小。依據以上理論，可得到下面的調試步驟。

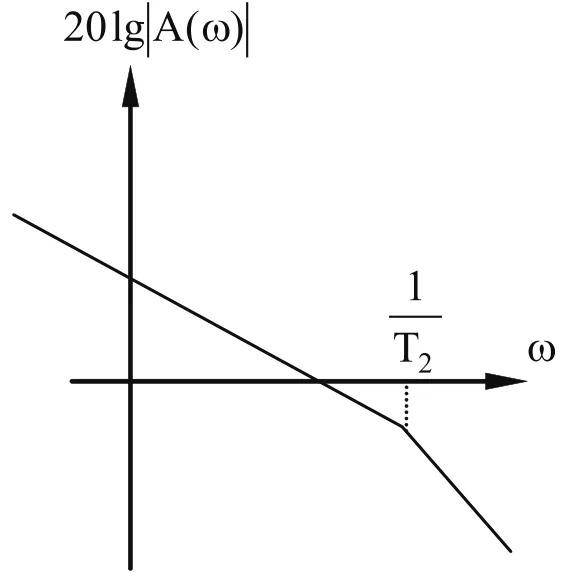
圖3 最佳二階系統的頻率特性

3 串聯校正系統參數的調試步驟

1）使R1＝0，C1足夠大（大到不振蕩），系統的頻率特性如圖2(C1)。階躍響應輸出波形如圖4所示：

圖4 電容足夠大積分校正系統的響應曲線

2）減小C1頻率特性上移，以提高快速性，使頻率特性變成圖2(a)所示，階躍響應如圖5所示，系統低頻輕微振蕩。

圖5 C1足夠小系統的階躍響應曲線

3）為消除振蕩同時提高系統的快速性可增大R1。當R1由0增加時，傳遞函數出現微分環節，時間常數由小到大。R1大到如圖3所示的頻率特性時，慣性環節時間常數T1和微分環節時間常數τ近似相等，這時在示波器上觀察階躍給定響應，輸出波形最大超調量不大為止，如圖6所示。調試完畢。

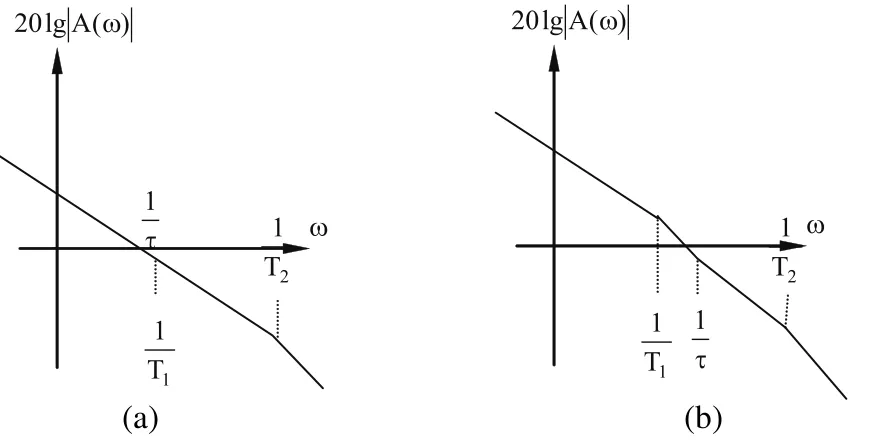
圖7 調試后的頻率特性

4 結束語

以上調試步驟能很快地、一次性地使系統具有快速、穩定的最佳二階性能指標。