發(fā)電機(jī)中間過熱時(shí)間常數(shù)對(duì)電力系統(tǒng)頻率動(dòng)態(tài)過程仿真影響
李宇龍,張晏銘,李 飛,王孜航,宋杭選
(1.東北電力大學(xué),吉林 吉林132012;2.河北邢臺(tái)供電公司,河北邢臺(tái)054000;3.哈爾濱電業(yè)局,黑龍江哈爾濱150030;4.黑龍江省電力科學(xué)研究院,黑龍江哈爾濱150030)
0 引言
頻率是電力系統(tǒng)運(yùn)行質(zhì)量和安全情況的重要指標(biāo)之一[1]。電網(wǎng)頻率的質(zhì)量,直接影響發(fā)電或者用電設(shè)備的運(yùn)行安全[2]。近幾十年,國(guó)內(nèi)外很多大電網(wǎng)崩潰事故都是由于頻率原因造成[3-6]。通過對(duì)發(fā)生事故時(shí)系統(tǒng)頻率動(dòng)態(tài)過程復(fù)現(xiàn)發(fā)現(xiàn),利用原系統(tǒng)模型獲得的頻率仿真動(dòng)態(tài)過程軌跡與實(shí)際事故時(shí)系統(tǒng)的頻率動(dòng)態(tài)過程軌跡存在較大的差異[7],這說明現(xiàn)階段使用的模型參數(shù)不夠準(zhǔn)確。因此,獲得一組相對(duì)合理的用于電力系統(tǒng)頻率動(dòng)態(tài)過程分析的模型參數(shù)成為現(xiàn)階段研究人員的主要目標(biāo)之一。基于此,本文提出了校核電力系統(tǒng)模型參數(shù)的一種新方法,即在發(fā)電機(jī)及其調(diào)速系統(tǒng)模型中引入蒸汽容積效應(yīng)中的過熱環(huán)節(jié),分析汽輪機(jī)中間過熱時(shí)間常數(shù)(以下簡(jiǎn)稱Trh)對(duì)電力系統(tǒng)頻率仿真動(dòng)態(tài)過程的影響,并通過實(shí)例驗(yàn)證汽輪機(jī)中間過熱時(shí)間常數(shù)能夠有效地修改系統(tǒng)頻率動(dòng)態(tài)仿真曲線回升斜率。
1 引入蒸汽容積效應(yīng)的頻率動(dòng)態(tài)過程模型
與文獻(xiàn)[8]中所采用的單機(jī)帶綜合負(fù)荷系統(tǒng)數(shù)學(xué)模型相比,本文采用的數(shù)學(xué)模型計(jì)及蒸汽容積效應(yīng),考慮了過熱環(huán)節(jié)中的中間過熱時(shí)間常數(shù),這對(duì)于電力系統(tǒng)頻率動(dòng)態(tài)分析具有更普遍的意義。為了便于分析系統(tǒng)中各參數(shù)的關(guān)系,忽略死區(qū)及限幅作用。考慮蒸汽容積效應(yīng)功-頻傳遞函數(shù)的框圖如圖1所示。
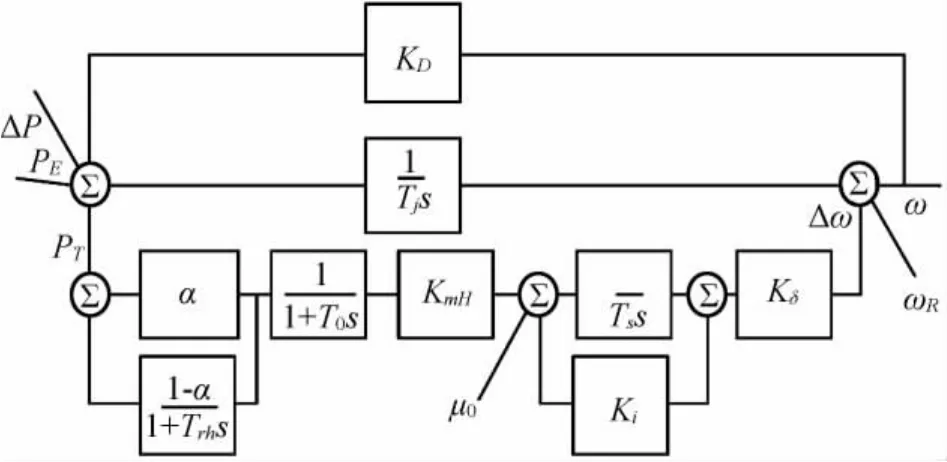
圖1 考慮蒸汽容積效應(yīng)功-頻傳遞函數(shù)框圖
系統(tǒng)中頻率變化與調(diào)速系統(tǒng)各參數(shù)變化的關(guān)系由式(1)表示。
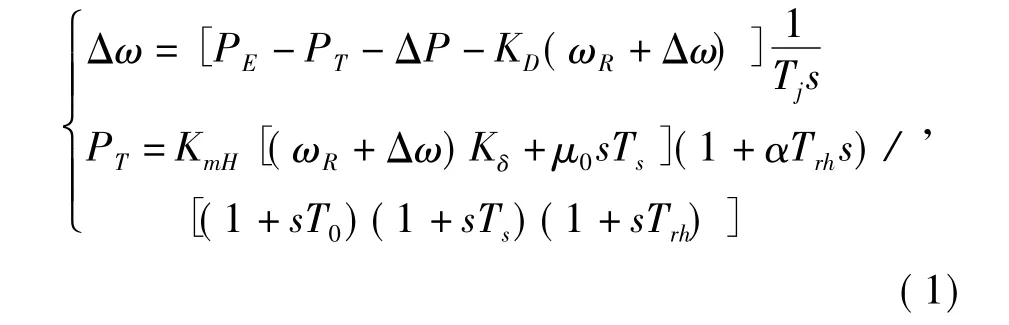
對(duì)上式公式進(jìn)行整理,可得:

式中,PE、ωR為標(biāo)幺值,Ki=1。
當(dāng)系統(tǒng)穩(wěn)定運(yùn)行時(shí),頻率變化量不變,即ΔP=0時(shí),Δω=0。所以,式(2)可進(jìn)一步簡(jiǎn)化為

Ts和T0的數(shù)量級(jí)遠(yuǎn)小于Tj和Trh的數(shù)量級(jí),忽略Ts和T0對(duì)系統(tǒng)頻率變化量的影響,最終可獲得:
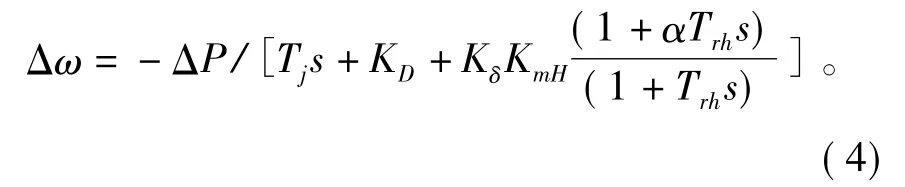
由式(4)可知,若計(jì)及蒸汽容積效應(yīng)以及忽略系統(tǒng)中非線性環(huán)節(jié),發(fā)電機(jī)中間過熱時(shí)間常數(shù)是影響系統(tǒng)頻率變化的主要參數(shù)之一。
2 實(shí)際系統(tǒng)中Trh對(duì)頻率動(dòng)態(tài)過程的影響
2.1 仿真工具
本研究采用中國(guó)電力科學(xué)研究院研發(fā)的《電力系統(tǒng)綜合分析程序》(PSASP for Windows)作為仿真工具。仿真系統(tǒng)中調(diào)速器模型采用程序中自帶的1型調(diào)速器。仿真過程中使用的數(shù)據(jù)是電力系統(tǒng)中采用廣域量測(cè)系統(tǒng)獲得的實(shí)測(cè)數(shù)據(jù)。
2.2 軌跡評(píng)價(jià)指標(biāo)
為了便于衡量系統(tǒng)參數(shù)變化時(shí),頻率仿真軌跡的變化情況,現(xiàn)定義如下3種用于評(píng)價(jià)軌跡特征的軌跡評(píng)價(jià)指標(biāo)。
1)頻降最低點(diǎn)fmin:指發(fā)生故障后頻率初始下降到最低點(diǎn)的值。fmin可以直接表征系統(tǒng)受擾程度,即:fmin越大,表明系統(tǒng)受擾程度越大。
2)頻降斜率Kd:指頻率初始變化點(diǎn)與頻率下降過程中斜率突變點(diǎn)之間的斜率。Kd只與發(fā)電機(jī)慣性時(shí)間常數(shù)與功率缺額大小有關(guān)。在相同轉(zhuǎn)矩的情況下,發(fā)電機(jī)慣性時(shí)間常數(shù)越大,轉(zhuǎn)子轉(zhuǎn)速改變?cè)铰l率下降時(shí)間就越長(zhǎng),下降的頻率幅值就會(huì)越小,系統(tǒng)阻尼振蕩的能力就越強(qiáng)[9]。
3)回升斜率Ke:指頻率回升了20%(fmaxfmin)的點(diǎn)與回升了80%(fmax-fmin)的點(diǎn)之間的斜率。Ke表征系統(tǒng)一次調(diào)頻能力。Ke越大,說明系統(tǒng)一次調(diào)頻能力越強(qiáng),系統(tǒng)可以越快的把跌落的頻率值拉回到允許的范圍內(nèi)。反之,Ke越小則系統(tǒng)一次調(diào)頻能力越差,系統(tǒng)拉升頻率值得速度將會(huì)越慢。
2.3 基于實(shí)際系統(tǒng)研究Trh對(duì)頻率動(dòng)態(tài)過程影響
以東北電網(wǎng)實(shí)際系統(tǒng)模型為例,研究發(fā)電機(jī)中間過熱時(shí)間常數(shù)變化時(shí),系統(tǒng)頻率仿真軌跡的變化規(guī)律。采用與文獻(xiàn)[8]中相同的算例,系統(tǒng)中共有152臺(tái)發(fā)電機(jī),總發(fā)電功率為20 571 MW,功率脫落241 MW,占總?cè)萘康?.17%,系統(tǒng)負(fù)荷模型采用50%恒阻抗,50%感應(yīng)電動(dòng)機(jī)。
改變系統(tǒng)中發(fā)電機(jī)中間過熱時(shí)間常數(shù)得到的系統(tǒng)頻率動(dòng)態(tài)仿真軌跡如圖2所示。
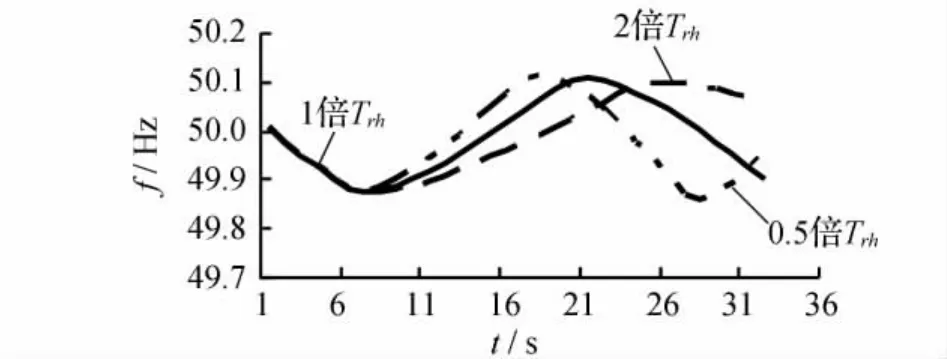
圖2 發(fā)電機(jī)中間過熱時(shí)間常數(shù)變化對(duì)頻率仿真軌跡的影響
由圖2可知,當(dāng)發(fā)電機(jī)中間過熱時(shí)間常數(shù)改變時(shí),系統(tǒng)頻率仿真曲線的最低點(diǎn)和回升斜率都做相應(yīng)改變。發(fā)電機(jī)中間過熱時(shí)間常數(shù)變化時(shí)的仿真軌跡評(píng)價(jià)指標(biāo)如表1所示。

表1 發(fā)電機(jī)中間過熱時(shí)間常數(shù)變化時(shí)的仿真軌跡評(píng)價(jià)指標(biāo)
當(dāng)Trh變化時(shí),軌跡指標(biāo)Kd不變,fmin變化很小,Ke變化較明顯。據(jù)文獻(xiàn)[9]顯示頻降斜率只與慣性時(shí)間常數(shù)有關(guān),所以增加發(fā)電機(jī)中間過熱時(shí)間常數(shù)并不影響頻降斜率。發(fā)電機(jī)中間過熱時(shí)間常數(shù)表征汽輪機(jī)出力達(dá)到額定值時(shí)所花費(fèi)的時(shí)間,所以在相同出力情況的條件下,發(fā)電機(jī)中間過熱時(shí)間常數(shù)越大,汽輪機(jī)出力達(dá)到額定值的時(shí)間越久,在系統(tǒng)頻率穩(wěn)態(tài)值不變的前提下,增大發(fā)電機(jī)中間過熱時(shí)間常數(shù),系統(tǒng)最終穩(wěn)定所需要的時(shí)間就越長(zhǎng),仿真頻率的回升斜率就越小;發(fā)電機(jī)中間過熱時(shí)間常數(shù)越大,汽輪機(jī)出力達(dá)到額定值的時(shí)間越久,則單位時(shí)間內(nèi)汽輪機(jī)出力將減少,用于抑制頻率曲線下降的能力將會(huì)降低,所以頻率最低點(diǎn)將會(huì)下降。
通過以上分析可知,發(fā)電機(jī)中間過熱時(shí)間常數(shù)的變化只對(duì)頻率仿真曲線回升斜率有較明顯的影響,所以,發(fā)電機(jī)中間過熱時(shí)間常數(shù)具有很優(yōu)秀的調(diào)節(jié)頻率仿真曲線回升斜率的能力。在擬合頻率動(dòng)態(tài)仿真曲線時(shí)可以充分利用發(fā)電機(jī)中間過熱時(shí)間常數(shù)這一特性。
3 算例分析
文獻(xiàn)[8]詳細(xì)地分析了慣性時(shí)間常數(shù)、調(diào)差系數(shù)、死區(qū)對(duì)系統(tǒng)頻率仿真曲線的影響。其中,慣性時(shí)間常數(shù)用于調(diào)整頻降斜率,調(diào)差系數(shù)用于調(diào)整仿真頻率軌跡的回升斜率,死區(qū)是用來調(diào)節(jié)頻率仿真曲線最低點(diǎn)。調(diào)差系數(shù)變化與系統(tǒng)頻率仿真軌跡變化的對(duì)應(yīng)關(guān)系,如圖3所示。
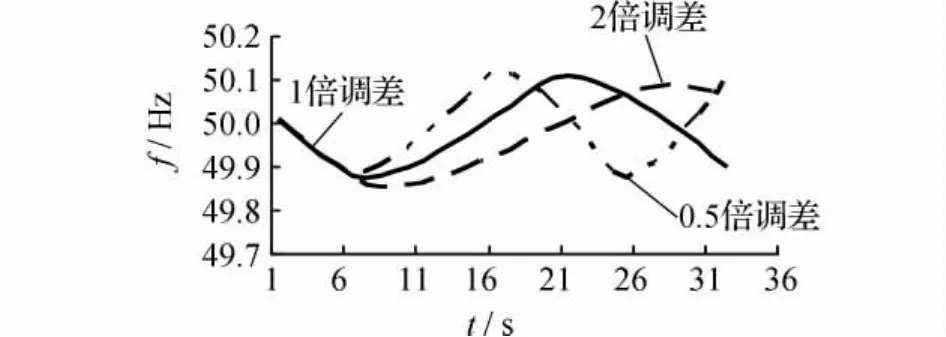
圖3 調(diào)差系數(shù)變化對(duì)頻率仿真軌跡的影響
從圖3中可知,當(dāng)調(diào)差系數(shù)改變時(shí),系統(tǒng)頻率仿真曲線會(huì)發(fā)生相應(yīng)的變化,其中,仿真頻率曲線最低點(diǎn)以及回升斜率的變化較明顯。調(diào)差系數(shù)變化時(shí)的仿真軌跡評(píng)價(jià)指標(biāo)如表2所示。
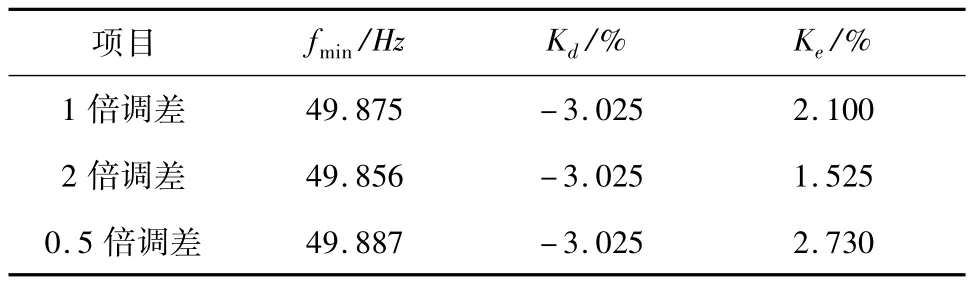
表2 調(diào)差系數(shù)變化時(shí)的仿真軌跡評(píng)價(jià)指標(biāo)
比較表1和表2中各軌跡指標(biāo)量,發(fā)現(xiàn)發(fā)電機(jī)中間過熱時(shí)間常數(shù)和調(diào)差系數(shù)做同樣倍數(shù)變化時(shí),兩者對(duì)于系統(tǒng)頻率仿真曲線回升斜率的影響比較接近;但若考慮其對(duì)于系統(tǒng)最低點(diǎn)的影響,發(fā)電機(jī)中間過熱時(shí)間常數(shù)的影響明顯小于調(diào)差系數(shù)的影響。發(fā)電機(jī)中間過熱時(shí)間常數(shù)更適合作為調(diào)整頻率仿真軌跡回升斜率的參數(shù)。
以汽輪機(jī)中間過熱時(shí)間常數(shù)代替調(diào)差系數(shù),重新制定參數(shù)調(diào)整方案。經(jīng)仿真計(jì)算后,只需調(diào)整慣性時(shí)間常數(shù)為原值的1.5倍,發(fā)電機(jī)中間過熱時(shí)間常數(shù)為原來的5倍,即可獲得與實(shí)際軌跡充分接近的頻率動(dòng)態(tài)仿真軌跡,校正參數(shù)后的仿真系統(tǒng)的頻率動(dòng)態(tài)過程如圖4所示。
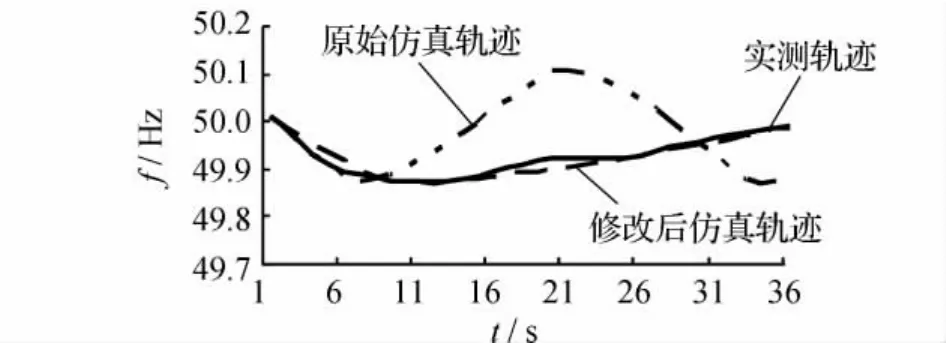
圖4 校正參數(shù)后的仿真系統(tǒng)的頻率動(dòng)態(tài)過程
實(shí)測(cè)曲線,基于原始參數(shù)的頻率仿真曲線以及基于修改后參數(shù)的頻率仿真曲線的具體軌跡評(píng)價(jià)指標(biāo)如表3所示。

表3 各曲線軌跡評(píng)價(jià)指標(biāo)
通過表3可知,修改發(fā)電機(jī)中間過熱時(shí)間常數(shù)同樣可以使頻率動(dòng)態(tài)仿真軌跡逼近于實(shí)際軌跡。與文獻(xiàn)[8]中采用的方法相比,由于慣性時(shí)間常數(shù)與發(fā)電機(jī)中間過熱時(shí)間常數(shù)變化對(duì)最低點(diǎn)影響都很小,若基于原始參數(shù)頻率仿真曲線的最低值與實(shí)測(cè)相同,則在調(diào)整參數(shù)過程中可以忽略系統(tǒng)仿真軌跡最低點(diǎn)的調(diào)整。
4 結(jié)論
在電力系統(tǒng)頻率動(dòng)態(tài)仿真過程中若引入蒸汽容積效應(yīng)環(huán)節(jié),則必須考慮發(fā)電機(jī)中間過熱時(shí)間常數(shù)。發(fā)電機(jī)中間過熱時(shí)間常數(shù)的改變對(duì)頻率仿真軌跡的頻降斜率無影響、對(duì)最低點(diǎn)影響很小、對(duì)回升斜率影響較大。與調(diào)差系數(shù)相比,在調(diào)整同等回升斜率的前提下,發(fā)電機(jī)中間過熱時(shí)間常數(shù)對(duì)于頻率仿真軌跡最低點(diǎn)的影響更小。這說明在引入蒸汽容積效應(yīng)環(huán)節(jié)的前提下,發(fā)電機(jī)中間過熱時(shí)間常數(shù)更加適宜用來調(diào)整頻率仿真軌跡的回升斜率。
[1]蔡邠.電力系統(tǒng)頻率[M].北京:中國(guó)電力出版社,1981.
[2]陳珩.電力系統(tǒng)穩(wěn)態(tài)分析[M].北京:中國(guó)電力出版社,1985.
[3]陳向宜,陳允平,李春燕,等.構(gòu)建大電網(wǎng)安全防御體系-歐洲大停電事故的分析與思考[J].電力系統(tǒng)自動(dòng)化,2007,31(1):4-8.
[4]印永華,郭劍波,趙建軍,等.美加“8.14”大停電事故初步分析以及應(yīng)吸取的教訓(xùn)[J].電網(wǎng)技術(shù),2003,27(10):8 -11,16.
[5]胡學(xué)浩.美加聯(lián)合電網(wǎng)大面積停電事故的反思和啟示[J].電網(wǎng)技術(shù),2003,27(9):2 -6.
[6]薛禹勝.綜合防御由偶然故障演化為電力災(zāi)難—北美“8.14”大停電的警示[J].電力系統(tǒng)自動(dòng)化,2003,27(18):1 -5,37.
[7]唐磊.汽輪發(fā)電機(jī)組調(diào)速系統(tǒng)動(dòng)態(tài)模型參數(shù)辨識(shí)與仿真研究[D].武漢:華中科技大學(xué),2009:1-76.
[8]劉洪波,穆鋼,徐興偉,等.使功-頻過程仿真軌跡逼近實(shí)測(cè)軌跡的模型參數(shù)調(diào)整[J].電網(wǎng)技術(shù),2006,30(18):20 -24.
[9]劉少華.基于頻率特性的低頻減載方案的校核研究[D].吉林:東北電力大學(xué),2010.

