基于DV-Hop的RSSI-Hop算法

李新玲，何加銘，2

(1.寧波大學通信技術研究所，浙江寧波 315211;2.浙江省移動網應用技術重點實驗室，浙江寧波 315211)

0 引言

無線傳感器網絡(Wireless Sensor Network，WSN)是一種全新的信息獲取和處理技術，確定事件發生的位置或獲取消息的節點位置是傳感器網絡最基本的功能之一，對傳感器網絡應用的有效性起著關鍵的作用［1］。

全球定位系統是目前應用最廣泛最成熟的定位系統，具有定位精度高、實時性好以及抗干擾能力強等優點，但是GPS定位并不適用于有遮擋物存在的環境［2］，節點能耗和體積較大，使用成本很高。在機器人領域中，機器人節點通常攜帶充足的能量供應和精確的測距設備，系統中機器人節點的數量很少，所以這些機器人定位算法不適用于傳感器網絡［3］。

無線傳感器節點通常隨機放在不同的環境中執行各種監測任務，節點的定位不依靠全局的基礎設施協助定位，配置低、能量少、可靠性差，測量距離時會產生誤差［4］，因此定位算法必須具有較好的容錯性，盡量減少節點之間的通信開銷，延長網絡的生存周期，并且每個節點分布式計算自身位置，而不是將所有信息傳送到某個節點進行集中計算。

本文提出的RSSI-HOP算法就是一種典型的與距離無關的定位算法，通過引用節點的RSSI強度來細化節點到信標節點之間跳數，從而相對提高節點定位精度。

1 無線傳感器網絡節點定位方法

現有的無線傳感器定位方法大致有2類:基于距離和距離無關定位［5］。基于距離定位指通過節點間測量距離或測量角度的輔助來進行節點定位的方法;距離無關定位指無需節點間的測量距離或相對角度、只依賴節點間連通信息的定位方法［6］。基于測距的方法能夠為傳感器提供一個精確的位置，然而，其對無線傳感器網絡節點的硬件要求也比較高，在一些應用領域，由于傳感器節點上硬件成本和限制，通常不使用基于測距的方法［7］，然而如何在低成本硬件基礎上實現大范圍定位的同時盡可能減少測量誤差，提高定位精度是當前定位技術面臨的主要困難。

1.1 距離無關定位方法

距離無關定位方法通過跳數來計算未知節點到信標節點的距離，有質心算法、APIT算法和DV-Hop定位算法。DV-Hop定位算法復雜度低，在各向同性網絡中具有較高的定位精度，并且可以覆蓋大范圍的監測區域，網絡部署成本低，目前已成為一種經典的距離無關定位方法。

1.2 DV-HOP

D.Nieulesu［8］等 人 提 出 的 APS(Adhoc Positioning system)系統采用的定位方法是:首先采用了經典的距離向量交換使所有網絡節點都能獲取到信標節點的以hop為單位的距離。每一個節點與其鄰居節點交互更新。第2階段，一個信標節點在與其他信標累積距離后，估計其平均每跳距離，并且將該平均單跳距離作為此信標節點的鄰居節點的標準部署校正。第3階段，任意節點在接收校正時，估計自己到信標節點的距離，以單位米表示，用于進行三邊測量。其中校正值的計算方法如下:

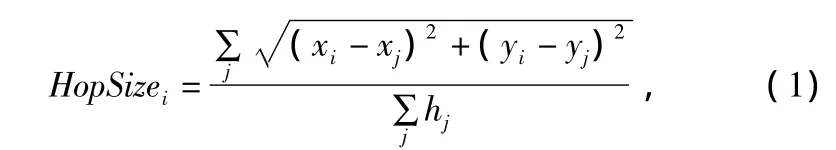
式中，(xi，yi)為第j個信標節點的位置;hj為從第j個信標節點到第i個信標節點的跳數。

如圖1所示，3個信標節點A與B、B與C、C與A之間的跳數分別為7跳、4跳和4跳，測量距離分別為100 m、65 m和80 m。則估計的網絡平均單跳距離為:(1065+80)/(7+4+4)=16.3 m。

1.3 RSSI

接收信號強度指示器(RSSI)是一種利用信號傳遞過程中強度衰減特征來進行距離估算的一種測距技術［9］。

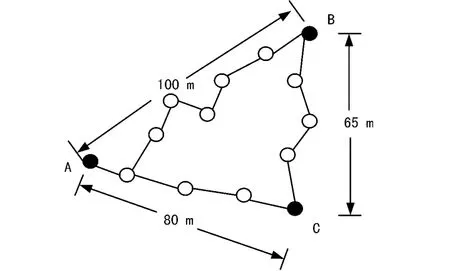
圖1 跳數信息估計網絡平均單跳距離示意圖

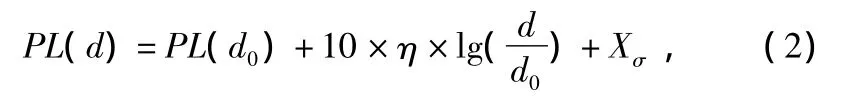
式中，PL(d)表示傳播距離d之后的信號強度損耗，以dB為單位;η是耗散系數(又名信號傳播常數)，用于指示耗散隨路徑增加的速率，通常取值為2～4;d0是從發射端附近測量的一個參考距離;Xσ是隨機環境噪聲，遵循X～N(0)。

從RSSI的耗散模型可看出，距離越近路徑耗散越小，在接收端測得RSSI值越大，距離越遠，耗散越大;在接收端測得RSSI值越小，因此可以使用節點間RSSI值來作為其距離大小的比征。在此引入RSSI測距技術，僅僅作為DV-HOP算法中的一種輔助定位手段，用于限制算法中的跳數和平均每跳距離值，在算法中并不進行基于RSSI的測距。

如果一個節點與它的鄰居節點之間視線連接，那么它的距離測量的平均誤差非常小。如果一個節點安裝在樹干上、坑井中，那么它的平均誤差將會非常大，因此不加選擇地使用RSSI來定位野外的傳感器將會產生較大的誤差。

由于無線信號在空間的傳播過程中隨著距離的增加，信號強度不斷下降，通過接收端測量信號強度的方式，就估算出發射端和接收端的距離。其理論路徑耗散函數如下:

2 RSSI-Hop算法

2.1 算法改進

在實際應用中，由于地勢不同，節點不均勻部署在監測區域中，導致傳感器節點部署不規則，一些節點有幾十個鄰居節點，而一些節點只有五六個鄰居節點，鄰居節點之間的距離也有很大差距，最短的幾米，而最長的可能有幾十米。非統一部署網絡中，由于標準DV-HOP算法通常會產生很大的誤差，如果2個節點到相同的信標節點有相同的跳數，那么他們的位置估計將會是相同的，這明顯與實際情況不符。

雖然由RSSI得到節點之間的距離有一定的測量誤差，但是節點之間的RSSI隨著距離的增加單調減小，仍具有參考價值。因此可以用RSSI來計算鄰居節點的關于RSSI的跳數，為了表達方便，稱之為RSSI跳數:

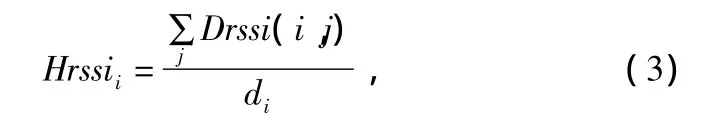
式中，∑jDrssi(i，j)表示節點到信標節點i的累積距離，Drssi(i，j)由路徑耗散函數計算而得，di表示信標節點i的平均單跳距離估計:

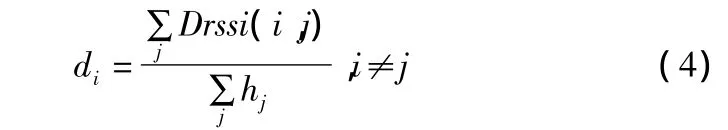
式中，hj為從第j個信標節點到第i個信標節點的跳數。

2.2 算法模型

①信標節點向鄰居節點廣播自身位置數據包:{xi，yi，hopcounti，hrssii}，其中(xi，yi)為信標節點 i的坐標，hopcounti為該節點到信標節點的以hop為單位的最短距離，hrssii為該節點到信標節點RSSI跳數，計算方法如式(3)所示。其中di是根據信標節點之間RSSI累積距離計算出來的平均單跳距離，由此得到的Hrssi節點間跳數信息作為參考，計算節點到信標節點之間的距離。根據RSSI距離在節點短距離視線靠近時接近真實距離，具有很高的參考價值。相反的，節點間距離較遠或有遮擋物時，RSSI距離較大，相應的距離信息也不準確，不具有參考價值，因此該處節點到信標節點跳數計算公式如下:

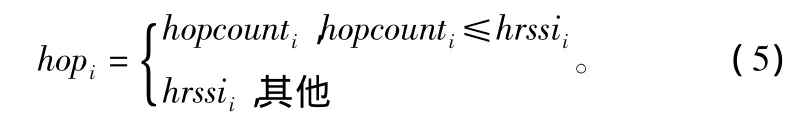
②計算該節點到信標節點i的距離ri，計算公式如下:

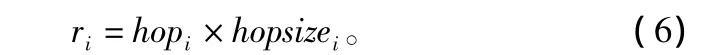
③當該節點與大于等于3個信標節點有距離估計時，利用三邊測量法估算出自身位置，并升級為附加信標節點參與后續迭代定位過程，輔助剩余節點定位。

3 仿真實驗

3.1 實驗設計

本文的實驗在OMNET平臺上進行，采用c++編程，節點分為信標節點和普通節點，hop by hop方式進行節點信息交互，估算節點到信標節點位置，為了監測本算法的性能，同時客觀獲取實驗結果數據，實驗數據由多次實驗獲取統計數據的平均值計算而得，所有節點均采取而為隨機部署方式進行部署。

3.2 實驗結果分析

在仿真中，節點隨機部署在500 m*500 m的方形區域中，設置節點的通信距離為30 m。信標節點個數為6，節點密度為6。選取其中100個節點的定位結果，比較結果如圖2所示。因為無線線路中的RSSI是非常不穩定的，并且對環境因素十分敏感，很難建模，因此在仿真時隨機選取50%的節點分布不均勻，且其平均相對測量誤差為20%。其余節點對之間的測量誤差較小。誤差較大的節點所占比例越多，表明網絡節點部署越不均勻，DV-hop中以跳數表示的節點到信標節點的距離也就也失真。

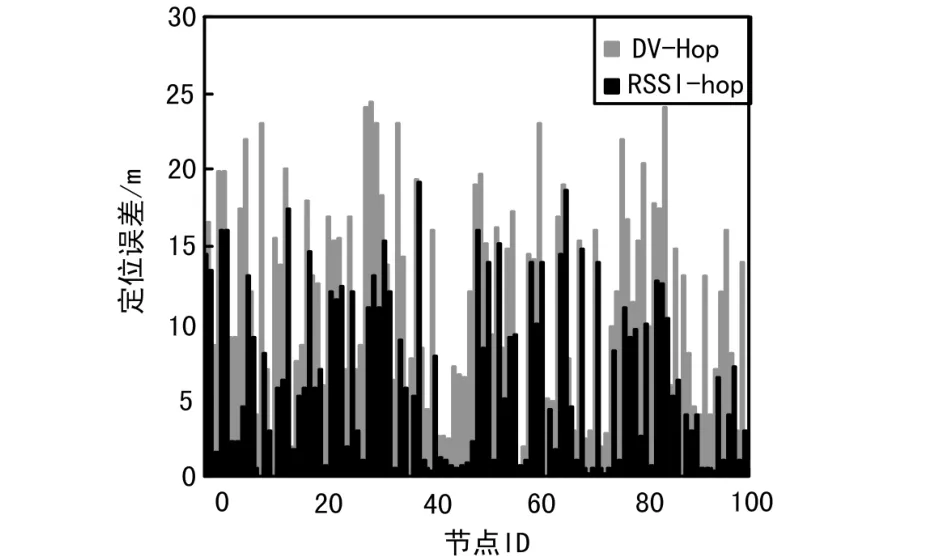
圖2 定位結果比較

如圖2所示，RSSI-Hop的定位誤差明顯減小，這表明，雖然由RSSI得到的距離估計存在一定的誤差，但是其在一定程度上仍能在一定程度上反映出節點分布狀況，由此得到的節點到信標節點的跳段距離更接近于真實距離。尤其當節點分布較為密集時，節點對越接近，由RSSI得到距離值越接近真實距離，得到的hop數就越真實。

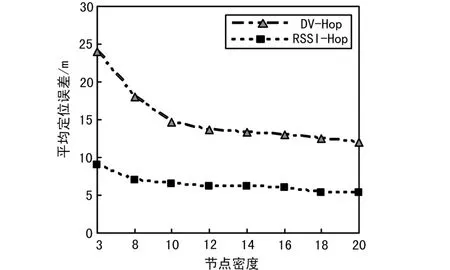
圖3 定位結果比較

當節點密度較低時，DV-Hop性能較差，這是因為節點不統一分布狀況明顯，跳數所表示的距離嚴重偏離真實值;當節點密度較大時，這一問題得到緩解，定位精度因此也提高了，尤其是節點密度由3增加到10時，平均誤差明顯下降。RSSI-Hop隨節點密度增加，Drssi(i，j)的相對誤差降低，由Hrssi(i)表示的距離更接近真實值，因此定位精度也隨之提高。當節點密度增加到一定程度之后，由于受到網絡中信標節點數量等因素的制約，節點平均定位誤差不再下降而是趨于平和。

4 結束語

通過分析經典的DV-Hop定位算法在計算節點到信標節點跳段距離的方面的不足，提出根據RSSI耗散模型的距離相關特性，引入Hrssi輔助估算各節點到信標節點之間的跳段距離，實驗證明該算法有效提高了網絡中節點密度較大區域節點定位精度，減少了由于節點到信標節點跳段距離相同而引起的定位沖突，提高了迭代效率，具有良好的定位效果。但是在障礙物大量存在的網絡，RSSI并不能很好地反應距離相關特性，不能明顯提高定位精度。

［1］TRIGONI N，KRISHNAMACHARI B.Sensor Network Algorithms and Applications［J］.Phil.Trans.Roy.Soc，2012(370):5-10.

［2］SCHMID J，BEUTLER F，NOACK B，et al.An Experimental Evaluation of Position Estimation Methods for Person Localization in Wireless Sensor Networks［J］.Lecture Notes in Computer Science，2011(6567):147-162.

［3］孫利民.無線傳感網絡［M］.北京:清華大學出版社，2005:148-155.

［4］AMUNDSON I，SALLAI J ，KOUTSOUKOS X，et al.RF Angle of Arrival-based Node Localisation［J］.International Journal of Sensor Networks，2011(9):209-224.

［5］COTARUIZ J，ROSILES J，ERNESTO S，et al.A Low-Complexity Geometric Bilateration Method for Localization in Wireless Sensor Networks and Its Comparison with Least-SquaresMethods ［J］.Sensors，2012(12):839-862.

［6］BOUKERCHE A，OLIVERIA H A B F，NAKAMURA E F，et al.Secure Localization Algorithms for Wireless Sensor Networks［J］.Communications Magazine，IEEE，2008(46):96-101.

［7］STANKOVIC J A，TIAN He.Energy Management in Sensor Networks［J］.Phil.Trans.Roy.Soc，2012(370):52-67.

［8］NICULESCU D，NATH B.DV Based Positioning in ad hoc Networks［J］.Journal of Telecommunication Systems，2003，22(1):267-280.

［9］WEI Xi，HE Yuan，LIU Yun-hao，et al.Locating Sensors in the Wild:Pursuit of Ranging Quality［C］∥New York:Proceedings of the 8th ACM Conference on Embedded Networked Sensor Systems，2011:295-308.