汽車傳動系扭轉振動建模與仿真分析

許在文， 萬海橋， 黃東東， 王 浩， 木 標

（1.安徽江淮汽車股份有限公司 底盤研發部，安徽 合肥 230601；2.合肥工業大學 機械與汽車工程學院，安徽 合肥 230009）

0 引 言

隨著汽車工業的發展，人們對汽車的各項性能要求越來越高，乘坐的舒適性作為一項直接反應乘客感受的指標，其重要性不言而喻，這就要求對汽車振動和噪聲進行有效的控制。造成汽車振動和噪聲的因素很多，其中動力傳動系的扭轉振動是引起汽車振動和噪聲的主要原因之一。由于扭振的監測相對比較困難，在分析和解決汽車振動時，扭振往往被人們忽略，只是在扭振破壞時，才加以考慮［1］。

因此，對傳動系的扭振建模和仿真研究，提前發現和解決扭振問題，對汽車的傳動系設計和匹配具有實際意義［2］。

1 扭轉振動力學建模

1.1 車型描述

本文以某車的傳動系為研究對象，建立其傳動系的扭振模型，并測試和仿真其扭振情況。該車為發動機后置橫置，發動機為直列四缸，傳動軸只有1根短軸，扭轉減振器采用傳統的離合器從動盤式。

1.2 模型簡化

由于實際分析需要，在盡量不影響仿真精度及可信度的情況下，建模時假設［3］：

（1）汽車剛起步時，模型的輸入可以簡化為在飛輪上加載一個脈沖信號，不考慮發動機本身復雜的各種諧次的激振。

（2）不考慮萬向節傳動動態特性對傳動系運動的影響和空間姿態的影響。

（3）驅動輪的輪胎與地面摩擦產生驅動力時輪胎的滑動率較低（可以看成純滾動）。

（4）忽略各種間隙，如齒輪間隙、萬向節間隙等因素的影響。

1.3 扭振力學模型

利用拉格朗日動力學方程建立傳動系各部件扭轉力學方程［4］。

飛輪：

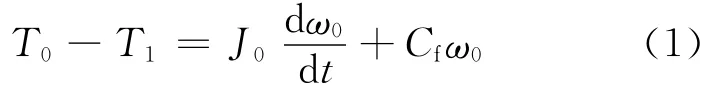
離合器：

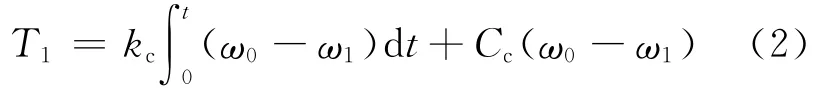
變速箱：

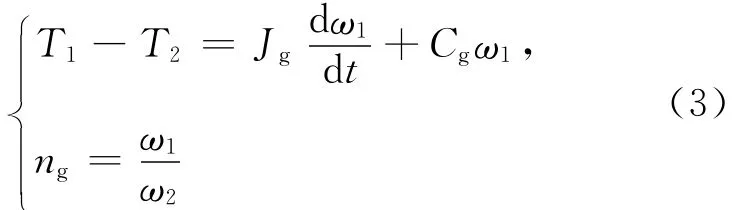
傳動軸：

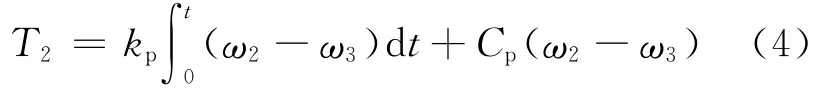
主減速器（包括差速器）：

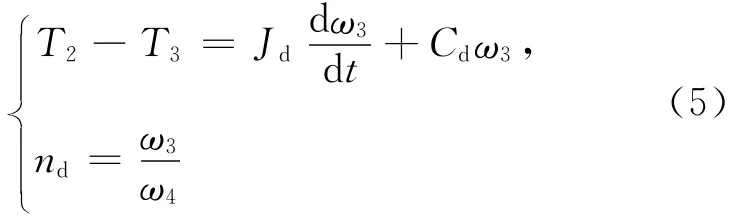
2個驅動半軸：

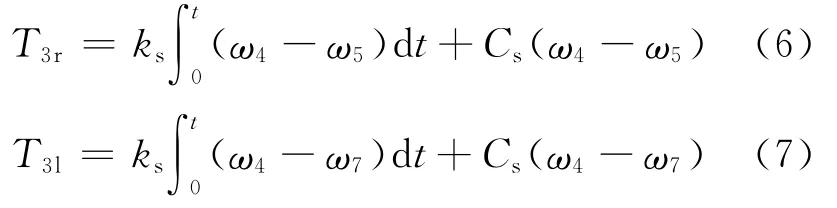
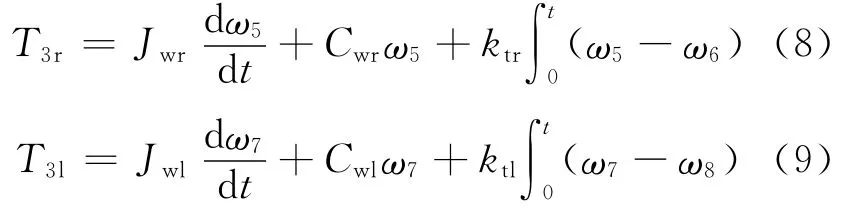
2個驅動輪：其中，T0為發動機輸入轉矩；Ti為傳動系部件i傳遞的轉矩；下標l和r分別代表左和右；Ji為傳動系部件i的等效轉動慣量；Ci為傳動系部件i的等效阻尼系數；ng＝6.602為變速器一檔速比；nd＝4.86為主減速器速比；ωi為傳動系部件i的角速度，i＝0，1，…，8；ki為傳動系部件的等效剛度系數。傳動系各零部件的參數值，見表1所列。

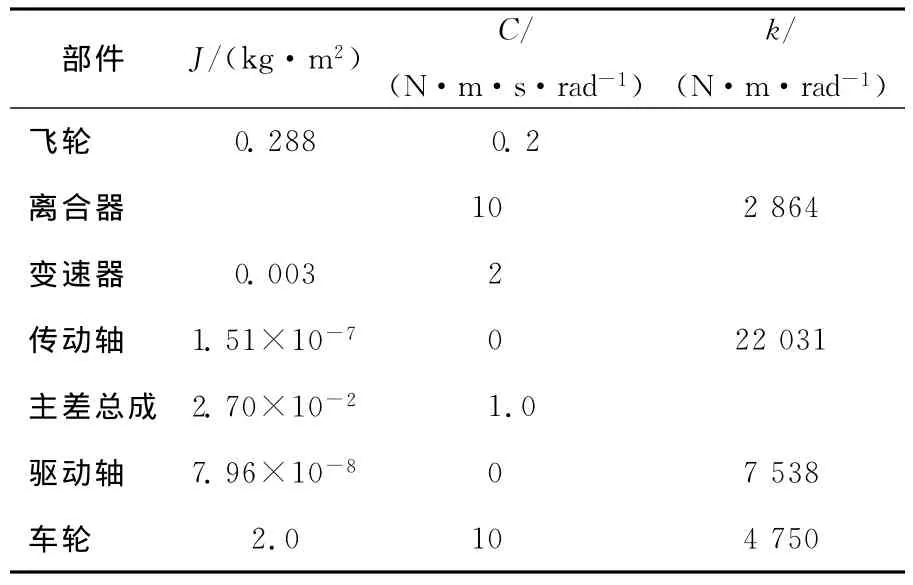
表1 傳動系部件參數

2 Simulink模型建立和仿真分析

2.1 模型仿真的建立

根據汽車傳動系扭振動力學方程（1）～（9），在Simulink仿真軟件中建立其仿真模型［5］，如圖1所示。

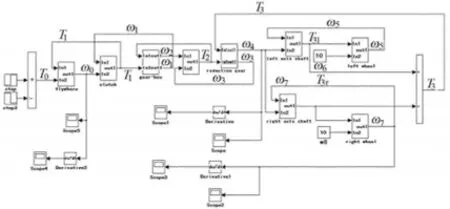
圖1 傳動系扭轉仿真模型

模型的輸入為在飛輪上加上150N·m的脈沖轉矩，模擬汽車剛起步時的情況，其數值由發動機輸出外特性圖獲取［3］，仿真時間設為3s，采用定步長四階Runge－Kutta算法進行求解。在系統仿真模型中設置3個仿真輸出位置點：①差速器輸出處；② 車輪處；③ 皮帶輪。曲軸扭轉剛度大，因此，可認為皮帶輪的扭轉振動角就是飛輪的扭轉振動角。

本文在皮帶輪處布置了扭振測量裝置，飛輪處由于安裝不便沒有布置，在飛輪處布置輸出點進行模型驗證。

通過仿真計算可得到差速器及車輪處的角速度 （ω）、角加速度（ω′）時間歷程曲線，分別如圖2a、圖2b所示。

由圖2a、圖2b可以看出，在車輪和差速器處存在較明顯的扭振現象，對以上2點處的加速度－時間數值，進行快速傅里葉變換，得其功率頻譜圖，如圖2c所示。由于傳動系扭轉是由于車輪和差速器造成的，由圖2c發現在3.9Hz和203.1Hz時，車輪和差速器的功率譜皆出現峰值，因此可知此時汽車傳動系發生明顯的扭振現象。

圖2 差速器、車輪處仿真數值曲線

2.2 扭振實驗

為了驗證所建立模型的正確性，對實車進行了扭轉振動的測試。實驗設備采用東華公司的旋轉機械階次分析儀器，如圖3a所示，其信號采集器為非接觸式霍爾傳感器，如圖3b所示。

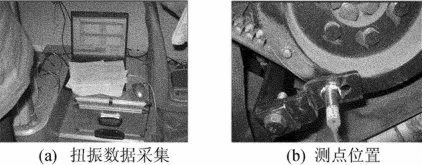
圖3 扭振實車測試

由于安裝不方便，本測試只在皮帶輪處安置了一個測點，如前文所述，曲軸的扭轉剛度大，所以皮帶輪處的扭振和飛輪處十分接近，故將皮帶輪處扭振測試數據和飛輪處的仿真結果進行比較，如圖4所示。

飛輪處仿真數據在4Hz處出現固有頻率，而實驗數據隨著轉速的升高，頻率并沒有增加［6］。在4Hz也出現共振，仿真結果和實驗比較接近，故可認為，所建立的仿真模型是正確的，可以進行分析優化計算。

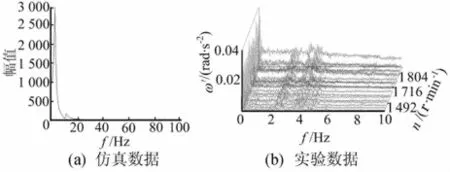
圖4 實驗數據與仿真數據的對比

2.3 靈敏度分析理論基礎

傳動系不計阻尼自由扭轉振動的特征方程可以表示為［7－9］：

（10）式對參數pm求導，得

其中，ωi為第i階固有頻率；θi為第i階正則化模態向量；J為傳動系質量單元所組成的轉動慣量矩陣；K為剛度矩陣。

2.4 主要部件參數化分析

2.4.1 轉動慣量參數化分析

利用所建立傳動系扭振動力學仿真模型，對傳動系中轉動慣量容易更改的部件，如飛輪、變速器、主差總成和左、右車輪的轉動慣量進行了參數化分析，結果如圖5所示。

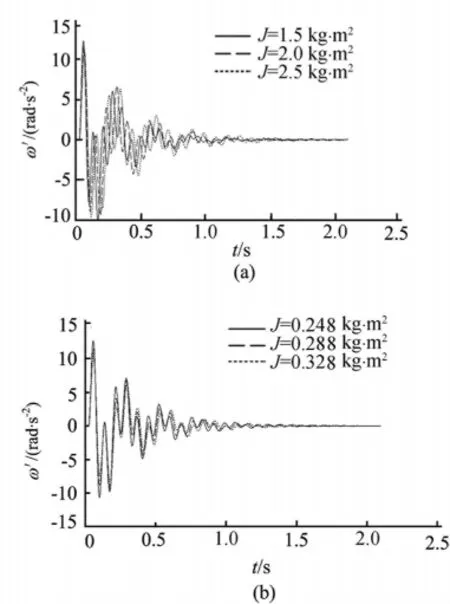
圖5 轉動慣量參數化分析

（1）左、右車輪轉動慣量對扭振系統低頻率影響分析。取Jω＝1.5、2.0、2.5kg·m2，仿真計算出差速器輸出點處的角加速度時間歷程，如圖5a所示。分析可知在轉動慣量增加時，扭振加速度減小，且扭振強度減小，而由頻率計算公式可計算出在相應的Jω下，所對應頻率分別為4.2、3.9、3.5Hz，此時振動頻率減小。

（2）飛輪轉動慣量的改變對扭振系統較高頻率影響分析。取轉動慣量參數為J0＝0.248、0.288、0.328kg·m2，仿真計算出差速器輸出點處的角加速度時間歷程，如圖5b所示。分析可知在轉動慣量增加時，扭振加速度減小，且扭振強度減小，計算其各自所對應的頻率分別為228、203、184Hz，可知此時振動頻率減小。

綜合分析可知，增大傳動系各部件轉動慣量會相應地降低系統發生扭振現象所對應的頻率和角加速度。

2.4.2 剛度系數參數化分析

對傳動系中傳動軸、驅動左、右半軸和左、右輪胎剛度系數進行參數化分析，如圖6所示。

圖6 剛度參數化分析

（1）左、右輪胎剛度系數對扭振系統影響。取kt＝4.00、4.75、5.75kN·m／rad，仿真出差速器輸出點處的角加速度時間歷程，如圖6a所示，可知隨著剛度增加，扭振加速度減小，扭振強度減小。計算上述剛度下所對應頻率分別為3.6、3.9、4.3Hz，即此時頻率增加。

（2）左、右半軸剛度系數對系統扭振頻率影響。取ks＝6.80、7.85、8.80kN·m／rad，仿真計算出差速器輸出點處的角加速度時間歷程，如圖6b所示，可知隨著剛度增加，扭振加速度增大，計算出所對應頻率分別為189、227、241Hz，即頻率也增大。

由此可見，通過增加傳動系各部件剛度，會相應地增加系統發生扭振的頻率，降低左右輪的扭振加速度，增加左右半軸的扭振加速度。

3 結束語

根據傳動系力學模型，在 Matlab／Simulink軟件中建立了傳動系的扭轉仿真模型。對車輛剛起步時傳動系扭振仿真計算時，可以觀察到傳動系中存在扭振現象及所對應頻率，在此基礎上對傳動系主要部件進行了參數化分析，指出了對扭振有重要影響的部件參數，通過對相應參數的修改，使得扭振降低。本文所建立的模型具有一定的通用性，參數的修改也比較方便，這種建模和分析方法為分析解決車輛傳動系扭振提供了參考。

［1］ 王 祺.內燃機軸系扭轉振動［M］.北京：國防工業出版社，1985：1－30.

［2］ 劉 云.雙質量飛輪系統扭振特性研究［D］.武漢：武漢理工大學，2009.

［3］ 任少云，孫承順，張建武.某牽引車傳動系起步扭轉振動動態 響 應 分 析 ［J］.上 海 交 通 大 學 學 報，2003，37（11）：1870－1873.

［4］ 范世典法A，鄂伯黑彌 M，柏特勒 H.車輛傳動系的扭轉振動的復合模型和仿真［J］.傳動技術，2003（3）：39－45.

［5］ 張德豐.Matlab／Simulink建模與仿真［M］.北京：電子工業出版社，2009：98－153.

［6］ 魏來生，趙春霞，張洪彥.某4×4車動力傳動系統扭振計算與試驗［J］.機械設計，2010，27（6）：56－59.

［7］ 邵毅敏，張 奎，李小俠，等.基于靈敏度分析的車輛傳動系統扭振分析及仿真［J］.長沙理工大學學報：自然科學版，2009，6（3）：1－5.

［8］ 劉 輝，項昌樂，鄭慕僑.車輛動力傳動系固有特性靈敏度分析及動力學修改［J］.汽車工程，2003（6）：591－594.

［9］ 曹文鋼，曲令晉，張代勝.某款半承載式客車車身有限元建模的分析研究［J］.合肥工業大學學報：自然科學版，2009，32（5）：620－623.