弱投射模與相伴弱投射模*
李劍華, 陳淼森
(浙江師范大學數理與信息工程學院,浙江金華 321004)
弱投射模與相伴弱投射模*
李劍華, 陳淼森
(浙江師范大學數理與信息工程學院,浙江金華 321004)
引進了弱投射模的概念,并在弱投射模上討論了Schanuel引理;同時,在弱投射模上定義了弱投射維數及弱整體維數,給出了弱投射維數為0和1時對模的刻畫;最后,在弱投射模的基礎上定義了相伴弱投射模,并得到相伴弱投射模的一些性質.
弱投射模;相伴弱投射模;弱投射維數;相伴弱投射維數;Schanuel引理
0 引言
投射模是同調代數與模論中的主要研究對象之一,對投射模及其性質的深入研究是模論里的重要問題.在對投射模的推廣得到新的模類的研究過程中,人們通常可以更深刻地認識投射模的內在結構.近年來,人們對投射模做了很多推廣[1-3].本文受到(P,M)-投射模定義[4]的啟發,定義了弱投射模,并在此基礎上定義了弱投射維數,討論了弱投射維數為0和1的模的性質;同時在弱投射模上討論了Schanuel引理等一些性質.
本文所涉及到的環R是有單位元的結合環,模均為左幺 R-模.相關概念及符號參閱文獻[5-6].
1 弱投射模
定義1設P,M,N為 R-模.若存在0≠g∈HomR(M,N),使得對于任意的 f∈HomR(P,N)且Im f?Im g,都有 h∈HomR(P,M),使 f=gh 成立,即有如圖1所示的交換圖,則稱P為M-弱投射模,g為P與N的相伴同態.
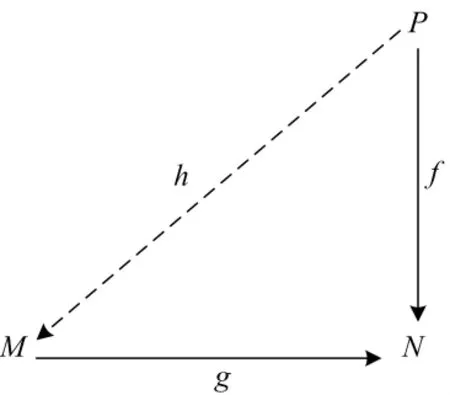
圖1 交換圖1
定義2若對于任意的R-模M,R-模P都是M-弱投射模,則稱P為弱投射模.
顯然,投射模為弱投射模.
Schanuel引理在模論研究中占有很重要的地位,筆者將在弱投射模上給出Schanuel引理.
定理1設 K1,K2,M 均為 R-模,P1,P2均為M-弱投射模,α∈HomR(P1,M)為 P2與 M 的相伴同態,β∈HomR(P2,M)為 P1與 M 的相伴同態,且有如下行正合列:
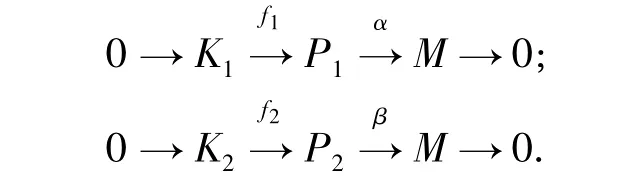
則 K1⊕P2?K2⊕P1.
證明 由定理 1的假設知 α∈HomR(P1,M).由于α,β均為滿同態,顯然 Imα =Im β.因為 P1為 M-弱投射模,所以存在 f∈HomR(P1,P2),使得 α = βf.同 理,存在 f'∈HomR(P2,P1),使得 β =αf'.直接由圖追蹤法知,必有 g ∈HomR(K1,K2),g'∈HomR(K2,K1) 使圖2可交換.
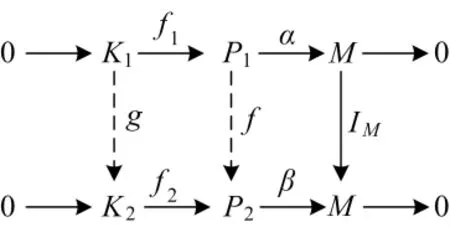
圖2 交換圖2
如圖3 所示,設 α1∈HomR(K1,K1⊕P2),α2∈HomR(P2,K1⊕P2)∈HomR(K2,K2⊕P1),∈HomR(P1,K2⊕P1)都為標準內射.由直和的泛性質知,必有 R-模同態 φ:K1⊕P2→K2⊕P1.同理,存在 R-模同態 φ':K2⊕P1→K1⊕P2,使得圖3可交換,即 φα2=',φα1=,φ'= α2f,=α1g'.再由直和泛性質所述的唯一性知φφ'=IK2⊕P1,φ'φ =IK1⊕P2.故 φ 為同構,即 K1⊕P2?K2⊕P1.定理 1 證畢.
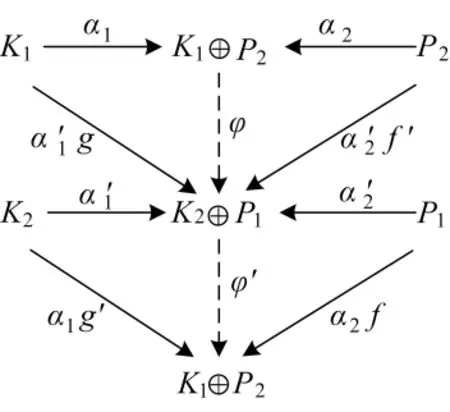
圖3 交換圖3
定理2設P若 P為弱投射模,則Pi(i∈I)為弱投射模.
證明 任取 i∈I,如圖4所示,設 λi∈HomR(Pi,P)為標準內射,ηi∈HomR(P,Pi)為標準投射.若存在g∈HomR(M,N)對任意的同態f∈HomR(Pi,N) 滿 足 Im f? Im g,令 φ =fηi∈HomR(P,N),則Im φ =Im fηi?Im f?Im g.因為P為弱投射模,所以存在 h∈HomR(P,M),使得φ=gh.再令h'=hλi∈HomR(Pi,M),有 gh'=ghλi=φλi=fηiλi=f,故 Pi為弱投射模.定理 2 證畢.
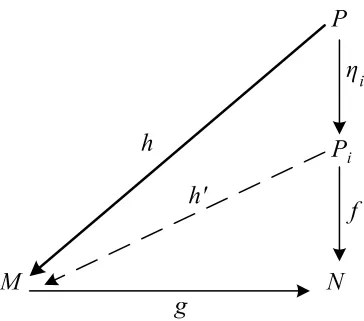
圖4 交換圖4
由文獻[1]知,對于任意的R-模M必有投射分解,故有以下引理:
引理1對于任意的R-模M,都有R-模正合列,
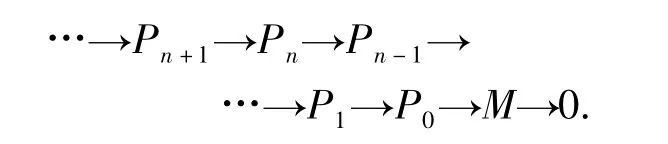
其中:Pi為弱投射模;i=0,1,2,….
于是可得如下定義:
定義3對于R-模M,若Pi(i=0,1,…,n)為弱投射模,則稱正合列…→Pn→Pn-1→…→P1→P0→M→0為M的一個弱投射分解.記M的弱投射維數為 Wlpd(M)=inf{n∈N|0→Pn→Pn-1→…→P1→P0→M→0};當 n不存在時,規定Wlpd(M)=∞.記 WlpD(R)=sup{Wlpd(M)|M為任意的R-模}為環R的弱整體維數.
定理3設M為R-模,則以下結論成立:
1)Wlpd(M)=0??M為弱投射R-模;
2)Wlpd(M)≤1??存在P0,P1為弱投射模,使得M?P0/P1;
3)WlpD(R)=0??每個R-模都是弱投射模.
證明 1)對于任意的R-模M,由弱投射維數的定義知Wlpd(M)=0??存在弱投射模P0,使得0→P0→M→0為M的弱投射分解??M?P0.因此,M也為弱投射模.
2)Wlpd(M)≤1??存在P0,P1為弱投射模,有正合列0→P1→P0→M→0??M?P0/P1.
3)由弱整體維數的定義知WlpD(R)=0??對于任意的R-模M,有Wlpd(M)=0,由1)可知這又等價于一切R-模都是弱投射模.
定理3證畢.
若P是投射模,對于給定的同態g:M→N,從P到N的任意同態都能提升到M,但當P是弱投射模時,以上結論不成立.下面對弱投射模定義中的能進行提升的同態組成的集合進行討論.
定理4設P為弱投射模,g:M→N為P到N的相伴同態,令 H=HomR(P,M),則gH={f|Im f? Im g,f∈ HomR(P,N)}.
證明 對于任意的同態f=gh∈gH,因為Im f=Im gh? Im g,
所以 f∈{f|Im f?Im g,f∈HomR(P,N)},從而gH ? {f|Im f? Im g,f∈ HomR(P,N)}.
因為P為弱投射模,所以{f|Im f? Im g,f∈HomR(P,N)}? gH,故
gH={f|Im f? Im g,f∈ HomR(P,N)}.定理4證畢.
2 相伴弱投射模
根據定義1,如果 P'也是M-弱投射模,那么存在g':M→N為P'與N的相伴同態,使得f'=gh'.一般來說,P'與N的相伴同態g'和P與N的相伴同態g不一定相同.現在考慮相同的情況,有以下定義:
定義 4[7]設 P,P',M,N 均為 R-模.若存在0≠g∈HomR(M,N),使得對于任意的 f∈HomR(P,N)且 Im f?Im g,對任意的同態 f'∈HomR(P',N)且 Im f'?Im g,都有 h∈HomR(P,M),h'∈HomR(P',M),使 f=gh,f'=gh'成立,則稱P與P'為相伴的M-弱投射模.
定義5若對于任意的 R-模 M,弱投射模P1,P2,…,Pn都具有相同的相伴同態,則稱 P1,P2,…,Pn互為相伴弱投射模.
定理5設弱投射模則 P 與 Pi(i∈I)為相伴弱投射模.
證明 設 g為 P與 N的相伴同態,λi∈HomR(Pi,P)為標準內射,ηi∈HomR(P,Pi)為標準投射,下證g為Pi與N的相伴同態.對任意的同態 fi∈HomR(Pi,N),滿足 Im fi?Im g,令 φ =fiηi∈HomR(P,N),且 Im fiηi?Im fi?Im g.因為P為弱投射模,所以存在h∈HomR(P,M),且φ=gh.再令 φ =hλi∈HomR(Pi,M),則 gφ =ghλi=φλi=fiηiλi=fi,所以 g 為 Pi與 N 的相伴同態,故P與Pi為相伴弱投射模.定理5證畢.
定理6設P.若 P1,P2,…,Pn為相伴弱投射模,則P為弱投射模.
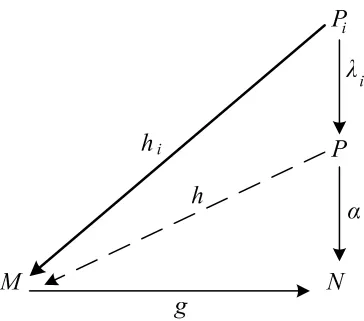
圖5 交換圖5
證明 如圖5所示,設 λi∈HomR(Pi,P)為標準內射,ηi∈HomR(P,Pi)為標準投射.因為 P1,P2,…,Pn為相伴弱投射模,所以存在一個相同的相伴同態 g∈HomR(M,N).對?α∈HomR(P,N)且 Im α?Im g,令 φ = αλi∈HomR(Pi,N),則有Im φ =Im αλi?Im α?Im g.因 Pi為弱投射模,故存在 hi∈HomR(Pi,M),使得 φ =ghi.由直和的泛性質知,存在同態 h:P→M,使得 hλi=hi成立,則αλi=ghi=ghλi.再由直和泛性質唯一性知,α=gh,所以P為弱投射模.定理6證畢.
由定理5和定理6可得以下推論:
推論1若P,P為弱投射模的充分必要條件是P1,P2,…,Pn互為相伴弱投射模.
推論2若 P1,P2為相伴弱投射模,則 P1,P2,P1⊕P2互為相伴弱投射模.
證明 設g:M→N為P1,P2的相伴同態,λi,ηi分別為標準內射、標準投射.下證g為P1⊕P2與 N 的 相 伴 同 態.對 任 意 同 態 f∈HomR(P1⊕P2,N)且 Im f?Im g,令 φi=fλi,則Im φi?Im f?Im g.又因為 Pi為相伴弱投射模,且g為其相伴同態,所以存在hi∈HomR(Pi,M),(i=1,2),使得 φi=ghi.令 h=h1η1+h2η2∈HomR(P1⊕P2,M),則
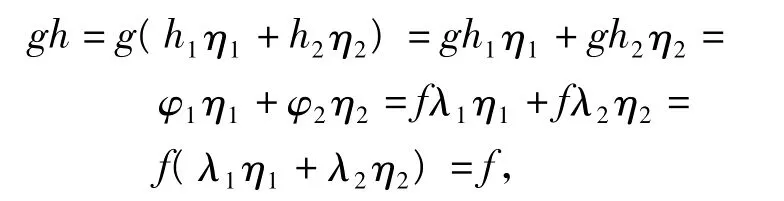
故g也是P1⊕P2與N的相伴同態,所以P1,P2,P1⊕P2互為相伴弱投射模.推論2證畢.
推論3若模正合列0→A→B→C→0可裂,則B是弱投射模當且僅當A,C是相伴弱投射模.
定義6對于 R-模 M,若 P1,P2,…,Pn互為相伴弱投射模,則稱…→Pn→Pn-1→…→P1→P0→M→0為M的一個相伴弱投射分解.記M的相伴弱投射維數為Awlpd(M)=inf{n∈N|0→Pn→Pn-1→…→P1→P0→M→0};當 n 不存在時,規定 Awlpd(M)=∞;記 AwlpD(R)=sup{Awlpd(M)|M為任意R-模}為環R的相伴弱整體維數.
類似地可得以下定理:
定理7設N為R-模,則有以下結論:
1)Awlpd(N)=0??N為弱投射R-模.
2)Awlpd(N)≤1??存在相伴弱投射模P0,P1,使得N?P0/P1;
3)AwlpD(R)=0??每個R-模都是相伴弱投射模.
命題1設 K1,K2,M 均為 R-模,P1,P2為相伴弱投射模,fi∈HomR(Ki,Pi)為單同態,且有如下正合序列:
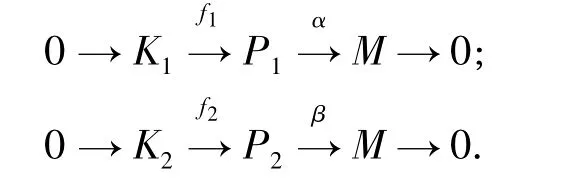
則 K1⊕P2?K2⊕P1.
證明 因為 P1,P2為相伴弱投射模,所以P1,P2必為弱投射模,且存在相同的相伴同態,有Im α =Im β.因此,K1,K2,P1,P2滿足定理 1 的條件,所以 K1⊕P2?K2⊕P1.命題1 證畢.
[1]Ahmad S.n-injective and n-flat modules[J].Comm Alg,2001,29(5):2039-2050.
[2]Bharadwaj P C.Small pseudo projective modules[J].International Journal of Algebra,2009,3(6):259-264.
[3]Kumar V,Gupta A J,Pandeya B M,et al.M-SP-projective modules[J].International Journal of Algebra,2011,5(12):563-568.
[4]張龍.弱內射模與弱內射維數[J].河海大學學報:自然科學版,2003,31(4):482-484.
[5]佟文廷.同調代數引論[M].北京:高等教育出版社,1998.
[6]Anderson F W,Fuller K R.Rings and categories of modules[M].New York:Springer-Verlag,1974.
[7]薛先貴,陳煥艮.相伴弱內射模[J].湖南師范大學學報:自然科學版,2007,30(1):10-13.
Weak projective module and adjoint weak projective module
LI Jianhua,CHEN Miaosen
(College of Mathematics,Physics and Information Engineering,Zhejiang Normal University,Jinhua Zhejiang 321004,China)
It was extended the concept of weak projective module and introduced the concept of weak projective module,the Schanuel lemma on weak projective module was discussed,the weak projective dimension and weak global dimension was defined,and the characteristics of the modules were discussed for weak projective dimension 0 and 1.Based on the weak projective module,the adjoint weak projective module was introduced and some properties of the adjoint weak projective module were obtained.
weak projective module;adjoint weak projective module;weak projective dimension;adjoint weak projective dimension;Schanuel Lemma
O153
A
2012-04-09
浙江省自然科學基金重點資助項目(Z6090150)
李劍華(1987-),男,浙江臨海人,碩士研究生.研究方向:代數學.
1001-5051(2012)03-0267-04
(責任編輯 陶立方)

