土介質中集團裝藥爆炸對不同模型混凝土破壞效應數值模擬
張千里,余 倩,甄樹新
(解放軍理工大學工程兵工程學院,江蘇南京210007)
混凝土是一種由沙石、水泥和水構成的脆性材料,具有良好的抗壓性能,現在已被廣泛地應用于各種防護工程上,因此對于混凝土的破壞研究是十分必要的[1]。土中爆炸對混凝土的沖擊作用是一個復雜的問題,涉及沖擊波的傳播,土和混凝土在高溫、高壓應變率條件下的動態力學行為,以及氣態爆轟產物和固態介質之間的、固態多層介質之間的相互作用問題[2]。
本文應用LS-DYNA3D有限元分析軟件,在裝藥結構、重量和體積不變的情況下,采用混凝土損傷模型和低密度泡沫模型,模擬土介質中裝藥爆炸后,沖擊波在混凝土中的傳播與衰減規律,為防護工程設計提供一定的參考依據。
1 計算模型建立
模型由炸藥、土體和混凝土板三部分構成,圖1為計算幾何模型示意圖。混凝土板尺寸400 cm×100 cm×10 cm;炸藥采用TNT集團藥包,耦合裝藥,在裝藥中心起爆藥包,其尺寸為20 cm×20 cm×10 cm;其余為土體。考慮到整個系統為軸對稱問題,只取模型的四分之一分析。
本模型中三種材料均采用Solid164三維實體單元,其中炸藥和土體采用Euler單元建模,單元使用多物質ALE算法,混凝土采用Lagrange單元建模,兩者通過耦合的方式作用。該算法優點是炸藥和土體在歐拉單元網格中流動,避免爆炸過程中網格的過分畸變對計算結果產生不利影響,并且通過流固耦合方式來處理相互作用,能方便地建立模型[3]。模型底部和右側采用無反射邊界,其他采用固定界條件,求解終止時間設為5 000μs,使用 cm-g-μs建模。
2 材料模型選用及參數
2.1 炸藥模型
本文采用HIGH_EXPLOSIVE_BURN材料模型和JWL狀態方程來模擬TNT炸藥。JWL狀態方程表達式為:
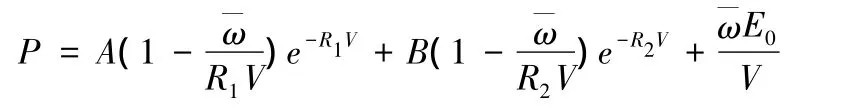
式中:P、E、V分別表示爆轟產物的壓力、單位體積的內能和比容(即單位體積裝藥產生爆轟產物的體積)。狀態方程中的系數 A、B、R1、R2、-ω 為描述 JWL方程的五個獨立物理常數。表1列出了TNT炸藥的主要參數,其中ρ為炸藥密度,PCJ為CJ爆轟壓力。
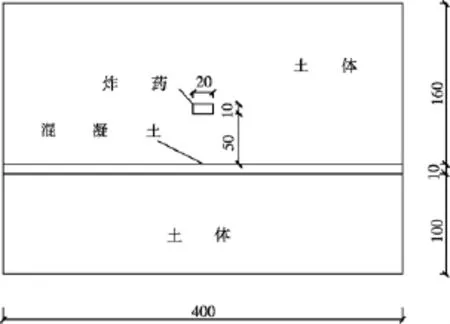
圖1 計算幾何模型示意圖(單位:cm)

表1 TNT炸藥主要材料參數
2.2 土介質材料
土介質采用土和可壓縮泡沫塑料模型(MAT_SOIL_AND_FOAM),即LS-DYNA3D中的5號模型,其塑性屈服極限函數采用如下公式為:

式中:a0,a1,a2為動力屈服常數,取值分別為 a0=340(MPa)2,a1=0.0703 MPa,a2=0.3;Sij為應力偏量;壓力 p是體積應變 εv(εv=ln(V/V0))的函數。土的密度1.98 g/cm3,剪切模量63.8 MPa,體積模量30 GPa。其余參數見參考文獻[4]。
2.3 混凝土模型
2.3.1 HJC模型
Holmquist T J,Johnson G R,Cook W H 于 1993 年提出Holmquist– Johnson-Cook(HJC)損傷本構模型[5]。HJC 損傷本構模型考慮了高壓、應變率及損傷;損傷計算了塑性體積應變,等效塑性應變及壓力的影響;通過體積應變計算壓力,并考慮材料壓實。其本構關系為:
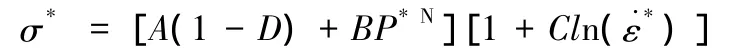
式中:σ為等效實際應力;p為壓力;fc'為靜態單軸抗壓
·強度;ε為參考應變率;A、B、N、C均為由實驗確定的常數;D為損傷系數;ΔεP為等效塑性偏應變增量;ΔμP為塑性體積應變增量;T為最大抗拉靜水壓力。混凝土HJC模型材料參數參見表 2[6]。

表2 混凝土HJC模型材料參數
2.3.2 低密度泡沫模型
研究表明[7]:低彈性模量、低密度的大變形彈塑性材料,在屈服應力基本不變的情況下,能產生很大應變。在LSDYNA3D中用Model57模型,材料參數參見表3[8]。

表3 低密度泡沫模型參數
3 數值模擬結果及分析
兩種模型介質中的裝藥結構都相同,為考察混凝土在爆炸作用下的變形能力,在距爆心下方105 cm處分別選取單元節點N44和單元節點N638(參見圖2),作其加速度時程曲線參見圖3。由圖3(a)可知爆炸發生后899μs內,加速度沒有顯著變化,隨著沖擊波的作用混凝土板向下運動,加速度開始變化,并隨時間的增加而增加,當時間為1 549.9μs時,模型2達到峰值為796.76 g,隨后加速度變化幅度逐漸減小,并逐漸衰減。而模型1變化幅度較大,并在2 149.3μs時,達到峰值為1 896.8 g。比較二者可以看出,模型2的加速峰值為模型1的42%,材料2大幅度地降低加速度峰值。在1 000 μs至2 500 μs內,模型2加速度整體變化幅度小于模型1。
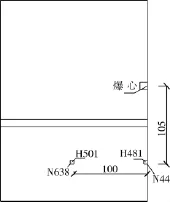
圖2 單元和節點位置(單位:cm)
由圖3(b)可知模型1的峰值加速度為168.49 g,而模型2的峰值加速度為142.64 g,后者是前者的84.6%,加速度峰值也顯著降低。由此可以得出,低密度泡沫模型能夠有效降低板下方介質的加速度,削弱沖擊波對介質單元的影響。

圖3 加速度時程曲線
同樣在距爆心下方100 cm處分別選取單元481和單元501(參見圖2),觀察其壓力變化。參見圖4(a)、圖4(b),可知模型2的壓力峰值比模型1小,且比模型1先達到峰值,其中圖4(b)中模型2峰值為0.597 MPa,是模型1峰值1.06 MPa的56%,即降低將近一半,達到峰值并后迅速衰減。由上述分析可以得知,低密度泡沫混凝土模型可以很好吸收沖擊波的能量,從而降低沖擊波對結構的影響,一些學者將這種模型混凝土作為隔震層,分析研究后發現,這種模型能夠吸收周圍介質的大部分能量,大幅度降低結構的加速度峰值,起到一定的隔震作用[9]。

圖4 單元壓力時程曲線
4 結論
比較集團裝藥非接觸爆炸形成沖擊波在混凝土及土介質中的傳播與衰減規律,了解兩種混凝土材料模型在沖擊荷載下的動態力學性能,并對沖擊波在混凝土和土介質中的傳播與衰減規律進行數值模擬。由模擬可知沖擊波對混凝土板的應變及周圍介質有較大影響,在相同條件下,低密度泡沫混凝土板變形大,吸收的應變能較多,并能夠減小結構的加速度和壓力峰值,從而削弱沖擊波對結構的沖擊響應。同時為隔震材料模型的選用及分析提供一定參考。
[1]宗琦,孟德君.煤系高嶺土巖石巷道掘進爆破技術優化[J].巖土力學,2004,25(6):984-987
[2]亨利奇.爆炸動力學及其應用[M].北京:科學出版社,1987
[3]白金澤.LS-DYNA3D基礎理論與實例分析[M].北京:科學出版社,2005
[4]趙均海,馮紅波,田宏偉,等.土中爆炸作用的數值分析[J].建筑科學與工程學報,2011,28(1):96-99
[5]Holmquist TJ,Johnson G R,Cook W H.A Computational Constitutive Model for Concrete Subjective to Large Strain,High Strain Rates,and High Pressure[C].14thInternational Symposium on Ballistics[C].Quebec City:American Defense Prepareness Association,1993:591-600
[6]王林,胡秀章,李永池.不同介質中集團裝藥爆炸混凝土沖擊響應的數值模擬[J].工程爆破,2010,16(4):5-9
[7]方秦,錢七虎.應力波與帶軟襯墊的地下結構動力相互作用[J].爆炸與沖擊,1988,8(4):289-298
[8]Crawford.R.E,Higgins.C.J,Bultmann E H.美國空軍防護結構設計與分析手冊[M].空軍后勤部工程設計局,譯.1980
[9]杜修力,廖維張,田志敏,等.炸藥爆炸作用下地下結構的動力響應分析[J].爆炸與沖擊,2005,26(5):474-480

