投影物鏡小比率模型的計算機輔助裝調

趙 陽 ，鞏 巖

(中國科學院 長春光學精密機械與物理研究所 應用光學國家重點實驗室，吉林 長春130033)

1 引 言

對于一般的光學系統，只要光機系統設計合理，加工滿足設計要求，裝調方案可行，就能較容易達到像質要求。然而這種裝調方法存在很大的盲目性，它要求裝調人員具備豐富的實際操作經驗，而且裝調的周期較長，精度不是很高。對于有超高精度要求、成像質量接近衍射極限的光學系統( 如光刻物鏡［1-2］、大口徑望遠鏡［3-5］) ，其光機結構設計、加工、裝調難度都很大，常規的裝調方法無法滿足像質要求，需要借助于計算機輔助裝調技術降低系統裝調的難度，指導裝調人員有針對性地對系統各種像差進行補償，最終得到滿足要求的光學系統。

目前文獻報道的計算機輔助裝調方法主要用于大口徑反射式光學系統［6-8］，由于光學元件數量較少，其位置誤差—失調量的個數也少。例如較復雜的離軸三反光學系統［9-10］，它由主鏡、次鏡和三鏡組成。主鏡通常作為裝調基準固定不動，整個系統的失調量由次鏡和三鏡的Z向移動、XY方向的偏心和傾斜共11 個參量組成。針對這些失調量，利用計算機輔助裝調技術，可以得到相對應的補償值，然后通過調節裝置將失調元件調整到理論設計位置。計算結果表明: 在失調量不大的情況下，補償量值和失調量值相接近，符號相反，表現出很好的收斂性和自洽性。然而，對于復雜的透射式光學系統，例如光刻物鏡，鏡片數量多達二十幾片，失調量個數多達數百項，不可能逐一去調節。即便是用于關鍵技術驗證的光刻物鏡小比率模型光學系統，鏡片數量為7 片，失調量個數也達到了35 項，逐一調節失調量也是不實際的。

本文以光刻物鏡小比率模型為研究對象，通過計算靈敏度矩陣，分析了偏心量和傾斜量之間的對應關系，有效減小了補償參量的數量。根據失調量的靈敏度，從系統中選出4 個補償參量。通過測量系統波像差，分析出系統存在的主要像差，再經過迭代計算，得到相應補償量值。然后，將得到的補償值代入軟件中進行仿真，驗證補償量計算結果的正確性。最后，調節補償元件對系統進行像質補償。復測結果表明，補償后的系統波像差( RMS) 由原來的50.864 nm 縮小到25.933 nm，優于40 nm 的技術指標要求。

2 計算機輔助裝調數學模型

計算機輔助裝調技術的應用首先要建立數學模型，確定光學系統的靈敏度矩陣，通過該矩陣找出對系統成像質量影響較大的失調量，將其選為補償量［11-13］。通過檢測光學系統波像差，利用軟件對測得的波像差進行處理，得到36 項Fringe Zernike 多項式系數，再次利用靈敏度矩陣對其進行奇異值分解，計算出各補償參量的調整方向和數值，用高精度驅動裝置調節補償參量，使光學系統成像質量滿足設計指標要求［14］。由此可見，計算機輔助裝調技術的基礎是靈敏度矩陣。

在數學上，像差是失調量的函數［15］。光學系統的像差用Fj(j=1，2，……，m) 表示，各失調量用xi(i=1，2，……，n) 表示，二者之間的函數關系表示為:

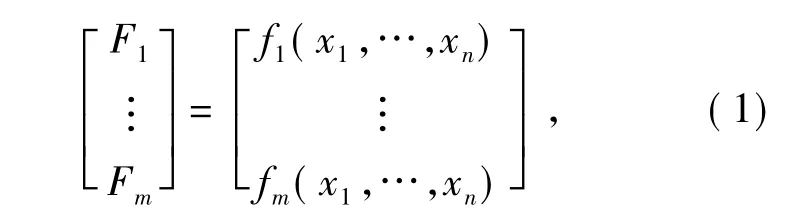
式中:fj(j=1，2，……，m) 表示像差與光學元件失調位置之間的函數關系。由于實際問題十分復雜，無法找出函數(f1，f2，……，fm) 的具體形式，因此把失調量與系統像質之間的函數關系近似地用線性方程來代替:

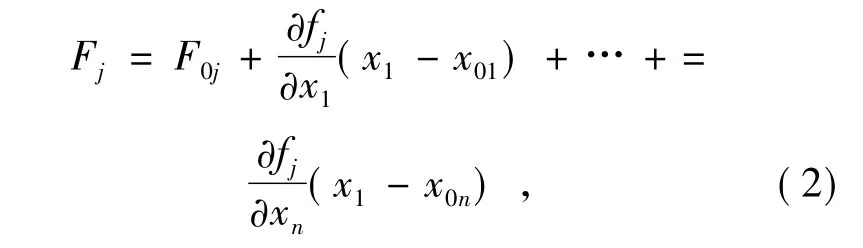
式中:F0j為系統優化設計后殘留的像差值，(xn-x0n) 為各光學元件由于誤差導致的失調量，Fj為系統波像差的測量值。由于已經線性近似，Fj可以用Fringe Zernike 多項式來表示。已知為像差對各個失調量的一階偏導數，為方便討論，這里用差來近似地代替微商，得到像差與失調量之間的近似線性方程組:

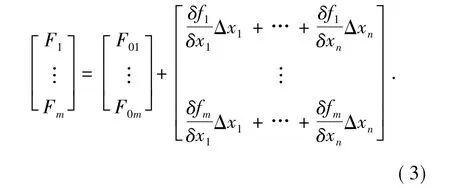
用矩陣形式來表示上述方程組，設

式中:ΔF 表示系統失調后的像質與理論設計值相比的變化量，Δx 表示失調量，A 表示靈敏度矩陣。當光學系統設計完成后，只要系統裝配時引入的失調量不是很大，靈敏度矩陣就唯一確定了，因此在光學系統設計階段就可以計算出靈敏度矩陣。

3 光刻物鏡小比率模型光學系統

與常規光學系統不同，光刻物鏡要求具有極小像差的成像質量。光學鏡片、機械結構零件的加工、裝調和檢測難度都是目前光學工程所能達到的極限水平［1］。例如，多數元件的裝調誤差都在μm 量級，個別元件甚至小于1 μm。雖然國內已經進口若干高精度機加設備，由于缺乏實際的裝調經驗，再加上國外的技術封鎖，我們只能逐漸摸索出一套光刻物鏡的集成方法。因此，在實際光刻物鏡制造之前，有必要進行一次甚至多次的物鏡驗證試驗，光刻物鏡小比率模型就是在這種情況下產生的，它的光學系統結構圖和技術指標要求如圖1 和表1 所示。

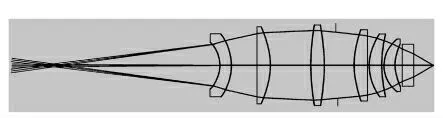
圖1 光刻物鏡小比率模型光學系統圖Fig.1 Chart of small scale projected objective for lithography

表1 光刻物鏡小比率模型技術指標要求Tab．1 Specifications of small scale projected objective for lithography

光學系統由7 片透鏡組成，材料全部采用紫外熔融石英玻璃，其理論成像質量如圖2 所示，從MTF 曲線可知系統已經達到衍射極限，系統最大波像差為10 nm RMS。

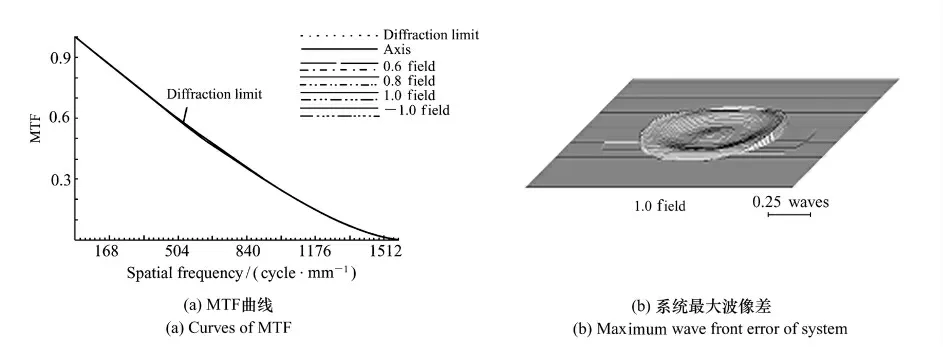
圖2 系統理論設計結果像質評價Fig.2 Image qualities of optical system by theoretical design

4 光刻物鏡小比率模型靈敏度矩陣計算

根據光學設計的公差分配要求，表2 列出了系統各項公差的最大值。計算靈敏度矩陣時失調量Δx要大于最大公差值，以保證靈敏度矩陣的準確性。Δx取值如下: 間隔/厚度取0.2 mm、偏心取0.2 mm、傾斜取1°。將Δx帶入到軟件中，得到失調后的波像差，用36 項Fringe Zernike 多項式擬合波面，其中全視場的Zernike 多項式系數分布如圖3所示。由圖可知由失調量導致的像質劣化主要體現在Zernike 系數的前9 項。此外，DSX、DSY分別與BTY、BTY有相近的靈敏度，而且Tip/Tilt 調節容易引入額外的Z向移動，因此系統的偏心補償量只在偏心失調量中選擇，減小了補償量選擇范圍。因此本文在分析時只討論前9 項Zernike 系數，并且非軸對稱失調量中只討論偏心量DSX、DSY。

表2 光學系統公差分配表Tab．2 Tolerance distributions of optical system

從圖3( a) ，( b) ，( e) 可知，對于相同的失調量0.2 mm，3#鏡有最大的偏心敏感性; 后截距和1#鏡與2#鏡間距都有較大的軸向像差敏感性，而其余失調量敏感性相對較小，因此補償量選為:1#鏡Z向移動、像面Z向移動和3#鏡X、Y方向偏心移動。需要說明的是:根據不同光學系統，都需要通過分析靈敏度矩陣，在敏感失調量中合理選擇補償量。

分別將失調前、后各視場Fringe Zernike 多項式系數和做幾何平均，就可以求得ΔF。根據式(3) 求出靈敏度矩陣A:

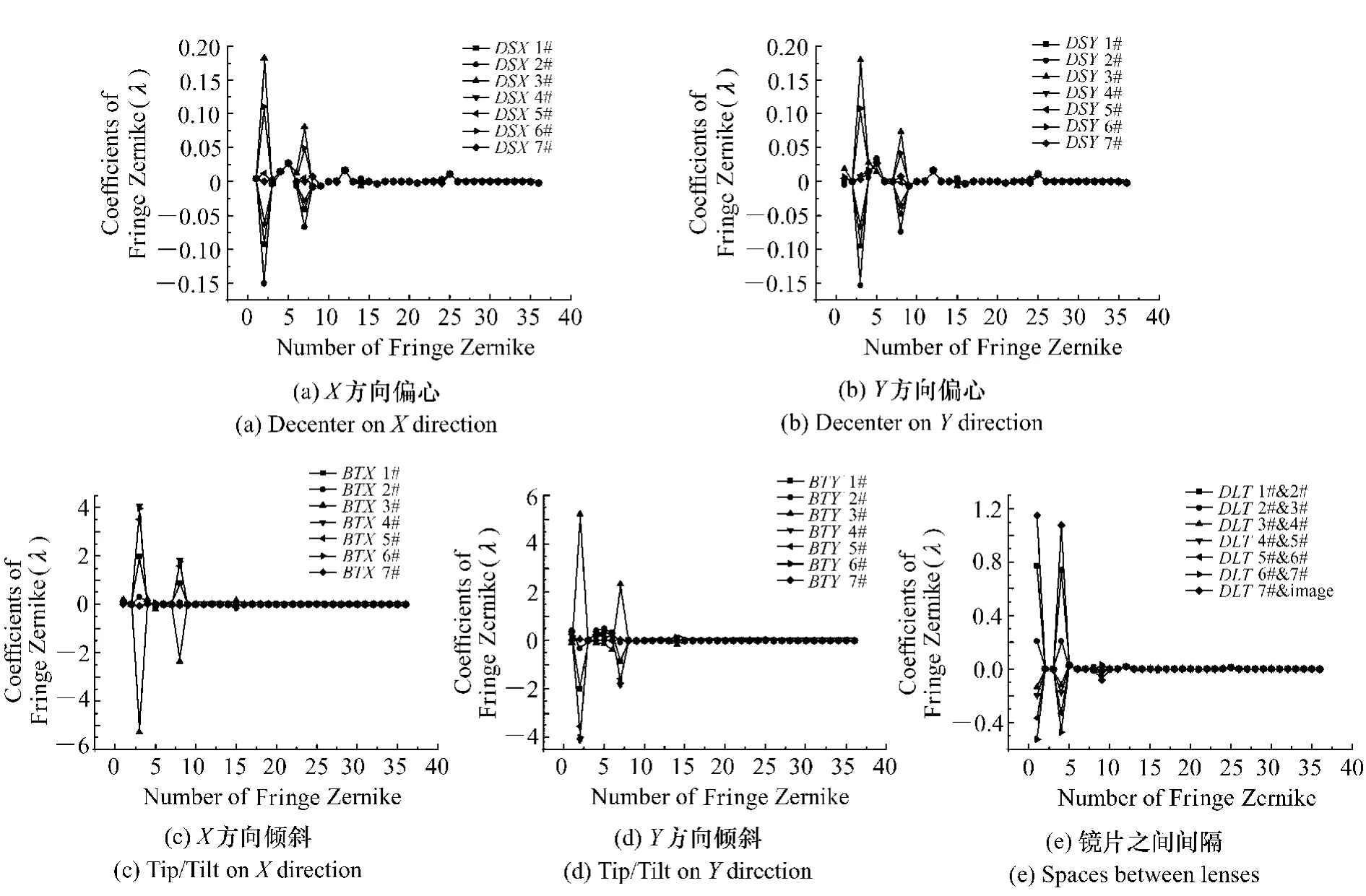
圖3 全視場波像差Zernike 系數分布Fig.3 Distributions of Zernike coefficients for wave front errors of edge fields of view

5 光刻物鏡小比率模型光機結構裝調

光刻物鏡小比率模型光學、機械零件加工完成后，鏡片面形偏差＜λ/10( RMS) ，機械件經過精修后的最大加工誤差為間隔公差0.1 mm，也滿足公差要求。使用高精度激光定心工作臺對其進行光機結構裝調，定心精度高達0.5 μm，這些對于得到高質量光學系統都是有利的。用ZYGO 干涉儀對其波像差進行檢測，檢測結果如圖4 所示。

由圖4 可知，系統波像差為50.864 nm( RMS) ，不滿足指標要求。波像差擬合的Fringe Zernike 多項式系數前9 項分布如表3 所示。可知Z7項(X方向三級彗差) 和Z9項( 三級球差)較大，需要進行偏心和Z向移動補償調節。雖然Z1～Z4值也較大，但它們主要體現了被測件擺放位置誤差和系統的離焦量，不能反映系統的真實波面性質，因此不予考慮。

圖4 用ZYGO 干涉儀測量系統波像差及測量結果Fig.4 Wave front error tested by ZYGO interferometer and testing results

表3 前9 項Zernike 系數分布Tab．3 The first nine coefficient distributions of Zernike

將所得的Zernike 多項式系數ΔF和補償參數Δx代入靈敏度矩陣，求得的系統補償量值結果如下: 1#鏡軸向移動量為+0.184 mm，3#鏡X方向偏心量為+ 0.03 mm，Y方向偏心量為+0.012 mm。其中X方向偏心補償量相對于Y方向較大，與表3中Z7項較大的結果是一致的。為進一步驗證計算結果的可靠性，將補償量代入到CODEV 中仿真，補償結果如圖5 所示，系統最大波像差為25.3 nm( RMS) ，滿足指標要求。

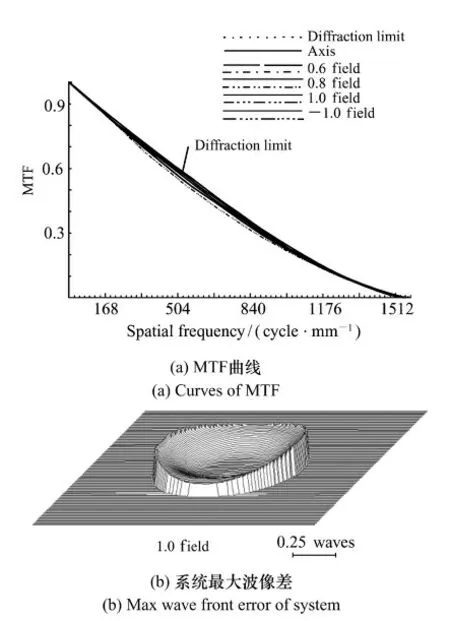
圖5 補償后的光學系統成像質量Fig.5 Image qualities after compensating

用干涉儀再次檢測補償后的光學系統波像差，結果如圖6 所示。系統波像差達到25.933 nm( RMS) ，優于指標要求，證明了這種計算機輔助裝調方法的正確性和可行性。

圖6 補償后系統波像差檢測結果Fig.6 Wave front error testing results after compensating

6 結 論

本文使用計算機輔助裝調技術對具有極小像差要求的光刻投影物鏡小比率模型光學系統進行了集成與像質補償，只選擇4 個補償量便使補償后的光學系統成像質量滿足設計指標要求，減少了光學系統的裝調難度。這種裝調方法適用于由多個光學元件組成的復雜光學系統的集成裝調，為高NA投影光刻物鏡光學系統的集成裝調提供了參考。

［1］ 王麗萍.極紫外投影光刻光學系統［J］.中國光學與應用光學，2010，3(5) :452-461.WANG L P. Optical system of extreme ultraviloet lithography［J］.Chinese J． Opt． Appl． Opt．，2010，3(5) :452-461.( in Chinese)

［2］ FLAGELLO D G，DE KLERK J，DAVIES G，et al.. Towards a comprehensive control of full-field image quality in optical photolithography［J］.SPIE，1997，3051:672-685.

［3］ 劉磊，李景林，呂清濤，等.大口徑反射光學系統裝調裝置設計研究［J］.光學 精密工程，2005，增1:134-137.LIU L，LI J L，LV Q T，et al.. Research on adjusting device of large aperture reflective optics system［J］.Opt． Precision Eng.，2005，S1:134-137.( in Chinese)

［4］ 孫敬偉，王建立，陳濤，等.地平式大口徑地基望遠鏡主光學系統裝調技術［J］.激光與紅外，2010，40(3) :233-237.SUN J W，WANG J L，CHEN T，et al.. Alignment technology of the large alt-azimuth ground-base telescope main optical system［J］.Laser＆Infrared，2010，40(3) :233-237.( in Chinese)

［5］ 李旭陽，李英才，馬臻，等.折軸三反射光學系統的計算機輔助裝調技術研究［J］.應用光學，2009，30(6) :901-906.LI X Y，LI Y C，MA ZH，et al.. Computer-aided alignment mothod of coaxial three-mirror-anastigmat system［J］.J． Appl．Opt.，2009，30(6) :901-906.( in Chinese)

［6］ 張庭成，王涌天，常軍，等.反射變焦系統的計算機輔助裝調［J］.光學學報，2010，30(6) :1688-1692.ZHANG T CH，WANG Y T，CHANG J，et al.. Computer-aided alignment for reflective zoom systems［J］.Acta Optica Sinica，2010，30(6) :1688-1692.( in Chinese)

［7］ LUNDGREN M A，WOLFE W L. Alignemnt of a three-mirror off-axis telescope by reverse optimization［J］.Opt． Engineering，1991，30(3) :307-311.

［8］ 孫敬偉，陳濤，王建立，等.主次鏡系統的計算機輔助裝調［J］.光學 精密工程，2010，18(10) :2156-2163.SUN J W，CHEN T，WANG J L，et al.. Computer-aided alignment for primary and secondary mirrors［J］.Opt． Precision Eng.，2010，18(10) :2156-2163.( in Chinese)

［9］ 陳欽芳，李英才，馬臻，等.離軸非球面反射鏡補償檢驗的計算機輔助裝調技術研究［J］.光子學報，2010，39(12) :2220-2223.CHEN Q F，LI Y C，MA ZH，et al.. Computer-aided alignment of off-axis aspheric mirrors in null testing［J］.Acta Photonica Sinica，2010，39(12) :2220-2223.( in Chinese)

［10］ 鞏盾，田鐵印，王紅.利用Zernike 系數對離軸三反射系統進行計算機輔助裝調［J］.光學 精密工程，2010，18(8) :1754-1759.GONG D，TIAN T Y，WANG H. Computer-aided alignment of off-axis three-mirror system by using Zernike coefficients［J］.Opt． Precision Eng.，2010，18(8) :1754-1759.( in Chinese)

［11］ 車馳騁，李英才，樊學武，等.基于矢量波像差理論的計算機輔助裝調技術研究［J］.光子學報，2008，37(8) :1630-1634.CHE CH CH，LI Y C，FAN X W，et al.. Research on computer-aided alignment based on vector aberration theory［J］.Acta Photonica Sinica，2008，37(8) :1630-1634.( in Chinese)

［12］ LIU J F，LONG F N，ZHANG W. Study on computer-aided alignment method［J］.SPIE，2005，5638:674-681.

［13］ 薛曉光，李國喜，龔京忠，等.面向裝配過程的精密光學系統計算機輔助裝調技術［J］.計算機集成制造系統，2011，17(10) :2163-2170.XUE X G，LI G X，GONG J ZH，et al.. Assembly process oriented computer aided alignment technology of precision optical system［J］.Computer Integrated Manufacturing Systems，2011，17(10) :2163-2170.( in Chinese)

［14］ YANG H S，KIM S H，LEE Y W，et al.. Computer aided alignment using Zernike coefficients［J］.SPIE，2006，6293:6293O1.

［15］ AGUROK I. Double expansion of wavefront deformation in Zernike polynomials over the pupil and the field-of-view of optical systems: lens design，testing，and alignment［J］.SPIE，1998，3430:80-87.