基于塊體集上限分析的錨板試驗模型探討

余生兵，黃茂松

（1. 同濟大學 地下建筑與工程系，上海 200092；2. 同濟大學 巖土及地下工程教育部重點實驗室，上海 200092）

1 引 言

錨板作為一種基本的抗拔承載力學模型，其抗拔承載力理論分析結果廣泛的應用于海洋錨板、抗拔基礎、埋置管線上浮和抗拔樁等問題的求解，因此，研究條形錨板的抗拔承載力對于求解這一類抗拔問題有著重要的工程意義。錨板模型試驗[1－12]作為一種研究錨板抗拔承載特性的方法，具有其他理論分析方法不可比擬的優點。但是，如果試驗模型的設計不夠合理，試驗結果往往不能正確地反映錨板真實的抗拔承載特性，這對于正確認識錨板的抗拔破壞機制是極為不利的。本文通過塊體集上限分析方法，研究了錨板的抗拔承載力和破壞面特性，并將分析結果與文獻中已有的模型試驗結果進行詳細對比，分析斜坡地形條件下現有模型試驗中拉桿對于錨板抗拔承載力的影響，并對錨板試驗模型的選取提出合理的建議。

2 現有錨板試驗模型簡述

圖1為錨板實驗模型示意圖。由圖1(c)可見，當錨板在拉力作用下移動時，與錨板運動方向相反的一側土體就處于卸荷回彈狀態，該側土體總是會隨錨板運動一段距離，然后再與錨板逐漸脫離。而當錨板埋置在滲透性較差的黏土中時，錨板頂面與底面的超靜孔壓差會形成一定的吸力，這將提高錨板的抗拔承載力，這就是錨板在拉拔過程中的“吸力”效應，因此，錨板抗拔承載力的發揮實際上與“錨-土”接觸面的脫離深度和吸力均密切相關。由于考慮“吸力”效應非常困難，很多學者[2,9,11,13]在考慮“錨-土”接觸特性時一般簡化為“立即脫離”和“無脫離”兩種條件。所謂“立即脫離”，是荷載施加之初錨板即與土體脫離，即完全消除“吸力”的影響，而“無脫離”則假定土體和錨板始終保持接觸，即認為“吸力”非常大，“錨-土”接觸面由于“吸力”的存在而始終沒有脫離。由于“錨-土”接觸面的脫離深度和吸力均受較多因素的影響，實際工程中很難確定其大小，而且吸力會隨著孔壓的消散而逐漸降低。實際工程中通常不考慮吸力對錨板抗拔承載力的影響，即采用“立即脫離”條件，所得結果是偏于安全的。

對于黏性土中的錨板，由于黏性土的滲透系數較小，在拉拔的過程中錨板底面的“吸力”效應非常明顯。為了更好地驗證現有理論分析的結果，很多學者[3－4]采用了如圖1(a)所示的試驗模型。該模型為了模擬“立即脫離”模式，一般采取將一個中空并接通大氣的有機玻璃盒子放在錨板的下面，以便使錨板底面與大氣相通，從而完全消除錨板底面吸力的影響。另一種消除錨板底面“吸力”效應的做法就是直接采用trapdoor模型[14]，即在模型箱底部開洞形成錨板的位置，該試驗模型是通過對錨板底面施加推力來模擬錨板的拉拔荷載的，如圖1(b)所示。

由圖 1(a)和圖 1(b)中這兩種試驗模型的示意圖可見，由于錨板底部的土體被移除了，這兩種模型試驗中錨板的破壞模式均被人為地限制為淺埋破壞模式，而不能自由過渡到深埋破壞模式，因此，這些模型試驗的結果中會出現條形錨板抗拔承載力系數大于11.42（深埋條形錨板抗拔承載力系數）的情況。有關塊體集上限法對于錨板深埋破壞模式和淺埋破壞模式的分析見文獻[15]，限于篇幅，此處不再詳述。

另外，一些學者[1,2]采用如圖1(c)所示的試驗模型來研究條形錨板抗拔承載力，采用這種試驗模型對試驗過程中錨板底面吸力的控制要求是非常高，在試驗過程中，多數情況下是采用控制加載速度來盡可能減少吸力的影響。Rowe[2]在其模型試驗中采用中空的拉桿對錨板施加拉力，中空的拉桿可以使錨板底面安裝拉桿的地方與大氣相通，這在一定程度上可以減少“吸力”效應的影響。對于砂土中的錨板，由于砂土的滲透系數較大，錨板底面的“吸力”效應不明顯，模型試驗中通常不予考慮，因此，砂土的模型試驗多采用圖1(c)所示的試驗模型。

綜上所述，除trapdoor模型可以不采用拉桿來施加拉力荷載外，其他試驗模型均需要采用拉桿來施加荷載。

3 塊體集上限分析方法

塊體集上限分析方法的基本思想是：集成和組合，即將最基本的三角形楔塊集成為兩個旋轉方向各異的旋轉塊體集（見圖2），然后，運用這兩個旋轉塊體集的不同組合來構造所求問題的運動許可速度場，并通過GAPS算法（遺傳-模式搜索算法）的優化得到最小上限解。筆者在文獻[15]中已經介紹了塊體集上限法求解過程。本文所采用的條形錨板運動許可速度場構造方式與文獻[15]中分析不排水黏土中條形錨板抗拔承載力所采用的構造方式相同，見圖3，即采用兩個組合塊體集上下累加構成，如圖3中①～④均為旋轉塊體集所示。如圖3中運動許可速度場的內能耗散和重力做功見文獻[15]，限于篇幅，此處不再詳細介紹。

圖3 淺埋條形錨板速度場構造示意圖Fig.3 Construction sketch of admissible velocity fields for shallow strip anchors

4 塊體集上限分析與模型試驗對比

4.1 地表水平條件下

地表水平條件下，本文塊體集上限分析解與模型試驗解的對比如圖 4所示。圖中，Nc0為不考慮土體重度時錨板的抗拔承載力系數；H為錨板埋深；B為錨板寬度；L為錨板長度。由圖4(a)可見，本文上限解與 Das[1]的模型試驗對比可以看出，本文塊體集上限解與Das的模型試驗解吻合較好。圖4(b)為本文塊體集上限解與 Rowe[2]的模型試驗對比。

如圖5所示，Rowe的模型試驗選用了7個不同尺寸的矩形錨板，并且進行了大量的模型試驗，由圖可以看出，Rowe的模型試驗結果雖然比較離散，但是該模型試驗結果的整體趨勢與本文塊體集上限分析的結果是非常吻合的。

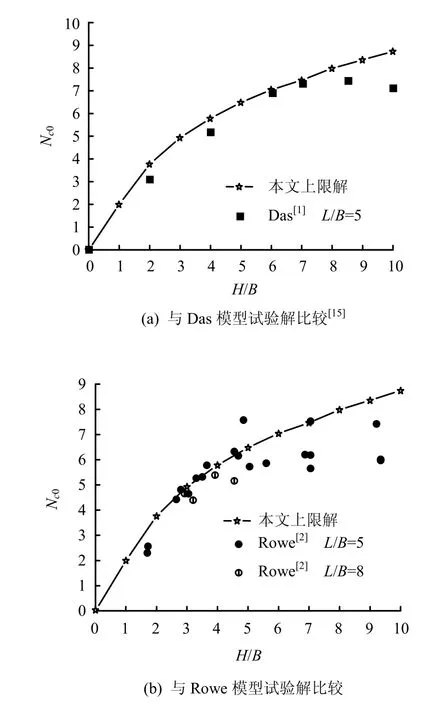
圖4 塊體集上限解與Rowe模型試驗解比較Fig.4 Comparison of pull-out capacities of block set mechanism and laboratory test

4.2 斜坡地形條件下

4.2.1 Khing等模型試驗

Khing等[3]通過模型試驗研究了飽和黏土中斜坡傾角對水平條形錨板抗拔承載力的影響，在其模型試驗中，錨板的寬度B = 7.6 cm，斜坡傾角β分別為 0°、10°、15°、20°、25°，采用的土體重度γ=17.1 kN/m3，不排水抗剪強度cu=10.2 kPa。Khing等的模型試驗所得到的結論與文獻[15]所得結論相同，即水平條形錨板抗拔承載力隨斜坡傾角的增大而減小。

為說明斜坡傾角對錨板抗拔承載力的影響，圖5中斜坡傾角分別為 0°和 25°時，塊體集上限分析計算結果與Khing等的模型試驗結果的對比，圖中Nc為考慮土體重度時錨板的抗拔承載力系數。由圖中可以看出，在地表水平條件下，本文計算結果與模型試驗非常吻合，而在考慮斜坡地形情況時（即斜坡傾角為25°時），Khing等的模型試驗結果與本文塊體集上限分析的理論預測相差較遠。由圖5可見，當斜坡傾角由0°增大到 25°時，模型試驗結果中錨板抗拔承載力的降低幅度遠遠小于塊體集上限分析的預測。由于該模型試驗結果較為離散，一些斜坡傾角為25°時的數據點甚至比斜坡傾角為0°時的結果還要大，這與Khing等的結論相去甚遠。筆者認為，由于各種原因該模型試驗并不是很成功。

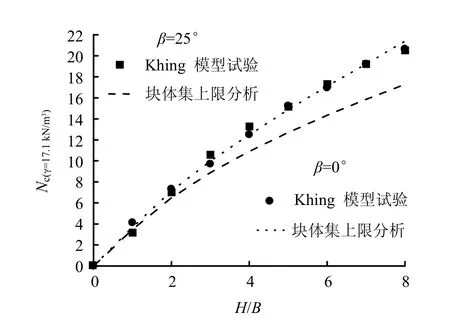
圖5 斜坡地形下塊體集上限分析結果與Khing的模型試驗結果對比Fig.5 Comparison of pull-out capacities of block set mechanism and Khing’s laboratory test results in sloped clayey ground

4.2.2 Rao和Prasad模型試驗

Rao和 Prasad[4]也通過模型試驗研究了黏土斜坡地形條件下圓形錨板的抗拔承載力，其模型試驗采用直徑為5 cm的圓形錨板。該模型試驗的所得的定性結論與文獻[15]所得結論相同，即錨板的抗拔承載力隨斜坡傾角的增大而降低。

由于Rao和Prasad的模型試驗采用的是圓形錨板，而本文塊體集上限分析研究的是條形錨板，因此，需要引入形狀系數將圓形錨板的抗拔承載力轉換為條形錨板的抗拔承載力。形狀系數S的大小與錨板的埋深比（H/B）等諸多因素有關，其定義見式（1）。

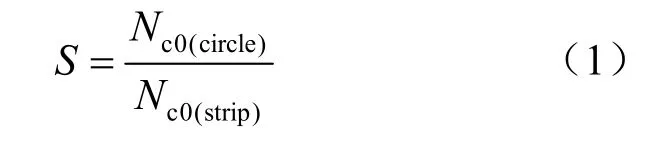
式中：Nc0(circle)、Nc0(strip)分別為圓形錨板和條形錨板的抗拔承載力系數。

Rowe和Davis[9]利用彈塑性有限元方法分別分析了圓形錨板和條形錨板的抗拔承載力。圖 6為Rowe和 Davis的彈塑性有限元分析結果，其中該分析采用的是k4破壞準則，即當錨板的位移等于彈性分析時所得到位移大小的4倍時，認為錨板處于極限破壞狀態。圖6中同時還給出了由該彈塑性有限元分析所得到的形狀系數S。

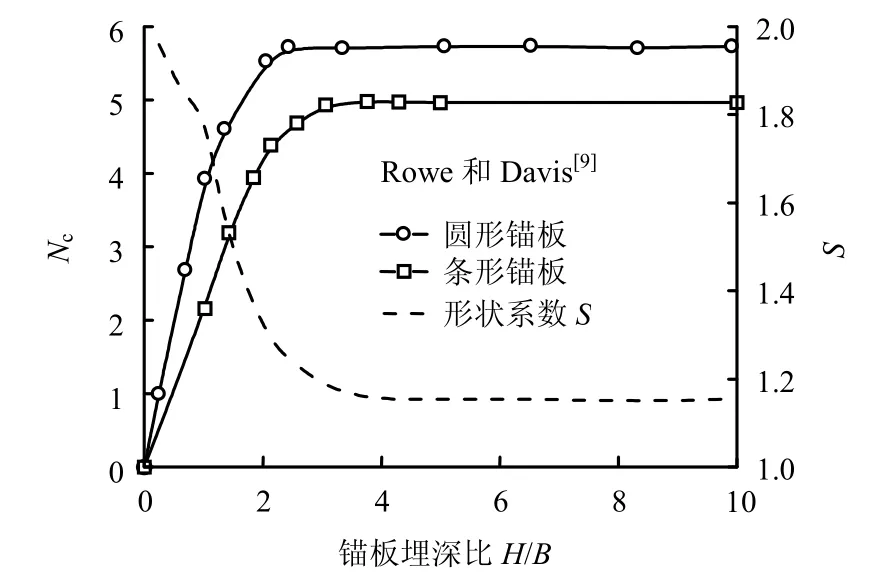
圖6 Rowe和Davis 彈塑性有限元分析所得到的形狀系數[9]Fig.6 Shape factors of Rowe and Davis[9]

鑒于前文地表水平條件下，塊體集上限分析結果與文獻中的模型試驗結果非常吻合。此處采用地表水平條件下（即斜坡傾角為 0°時），Rao和Prasad的圓形錨板模型試驗數據與本文塊體集上限分析所得到的條形錨板上限解相比，即由式（2）求得形狀系數S，如圖7中的黑色方塊點所示。圖 7中，D為圓形錨板的直徑；H/D即為圓形錨板的埋深比，對于水平條形錨板而言，其錨板埋深比為H/B。同時，圖7中分別給出了Merifield等[16]采用三維下限有限元分析得到的形狀系數，以及由Rowe和Davis[9]的彈塑性有限元分析所得到的形狀系數。由圖可以看出，極限分析下限有限元分析得到的結果偏于保守，而本文的形狀系數與Rowe和Davis的彈塑性有限元分析結果較為接近。

為便于應用，本文對由式（2）求得的形狀系數S數據點進行了擬合，得到了本文所采用的形狀系數計算公式：

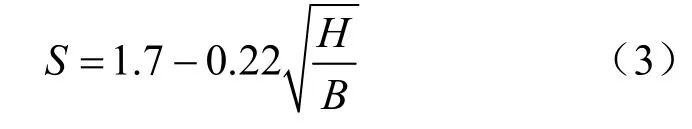
當式（3）求得形狀系數S＜1.15時，取S = 1.15。采用式（3）所示的形狀系數，在斜坡地形條件下，本文塊體集上限分析解與Rao和Prasad[4]的圓形錨板模型試驗對比如圖8所示。圖8中，陰影部分表示當斜坡傾角由0°增大到45°時，塊體集上限分析中錨板抗拔承載力的降低程度。由圖可見，當錨板埋深比H/B比較小時，本文塊體集上限分析預測與模型試驗結果是比較吻合的，而H/B比較大時，模型試驗結果中斜坡傾角的影響逐漸變小。如圖8所示，當斜坡傾角為45°時，隨錨板埋深比H/B的增大，其抗拔承載力與地表水平時相比差距逐漸變小。當 H/B＞4時，模型試驗結果甚至出現了兩條線基本重合的現象。對于模型試驗而言，這說明在錨板埋深比比較大時，斜坡傾角對錨板抗拔承載力會降低到甚至可以忽略的程度，這一結論與本文塊體集上限分析的理論預測完全相反。

圖7 圓形錨板與條形錨板的形狀系數Fig.7 Shape factors of circle and strip anchor plates

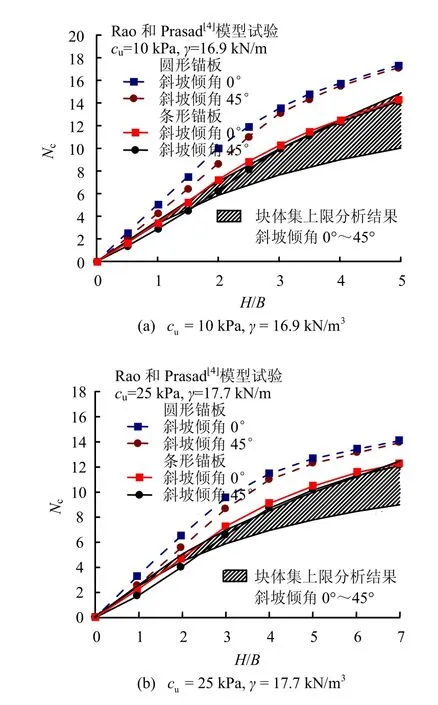
圖8 斜坡地形下本文上限解與Rao和Prasad模型試驗的對比Fig.8 Shape factors of circle and strip anchor plates

5 試驗模型中拉桿的影響

Rao和 Prasad[4]模型試驗中之所以會出現與本文塊體集上限分析理論預測相反的情形，主要是該模型試驗采用了圖 1(a)試驗模型，試驗過程中拉拔力通過連接在錨板中點的金屬拉桿來實現。因此，錨板的埋深比H/B越大，該金屬拉桿在土體中埋置的長度就越大。而對于斜坡地形條件下塊體集上限法對于錨板破壞面的分析結果，如圖9所示。由圖可以看出，當地表水平時，破壞面呈現對稱的 U型，且拉桿處土體變形主要是豎直方向的。當斜坡傾角存在時，破壞面向坡腳方向傾斜，因此土體變形會傾向于向坡腳方向傾斜，原先在地表水平條件下所呈現的對稱性不復存在。同時，由圖9還可以看出，斜坡傾角越大，破壞面向坡腳方向的傾斜程度也越大。

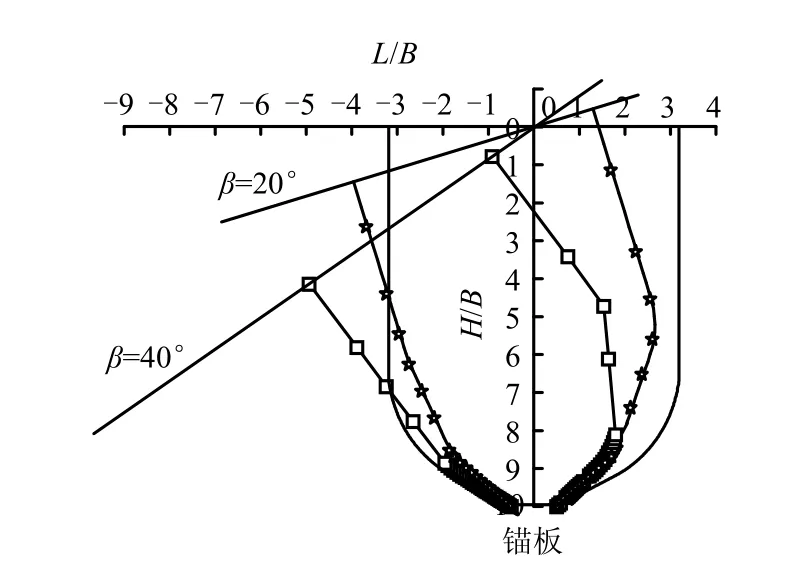
圖9 不同斜坡傾角時水平條形錨板破壞面(H/B=10)[15]Fig.9 Failure surface of strip anchor plate at different slope angles (H/B=10)[15]

由圖10(a)所示，對于地表水平條件下，由于模型試驗中拉桿正好處于錨板破壞面的對稱軸的位置，因此，拉桿對錨板抗拔承載力的影響主要體現在拉桿側壁與土體的摩擦阻力上，當拉桿表面足夠光滑時，摩擦阻力的影響完全可以忽略不計。而對于斜坡地形條件下（見圖10(b)）可以明顯的看到，拉桿的存在對土體向坡腳方向的變形有著明顯的制約作用，因此拉桿的存在可以提高錨板抗拔承載力。由塊體集上限分析可知，斜坡傾角和錨板埋深比H/B越大，錨板破壞時破壞面向坡腳方向的傾斜程度也越大，這就意味著土體在拉桿側壁的法向方向的變形也越大，即拉桿對錨板抗拔承載力的貢獻也越大，這就導致了Rao和Prasad[4]模型試驗結果中，隨著錨板埋深比H/B的增大，斜坡傾角對錨板抗拔承載力的降低部分越來越多的被拉桿的有利貢獻所抵消。因此，Rao和Prasad模型試驗所測得的試驗數據實際上是錨板與拉桿協同作用下的抗拔承載力，這與研究錨板本身抗拔承載力的試驗目標有著很大的區別。因此，由于拉桿的存在，Rao和 Prasad[4]的模型試驗對于斜坡地形條件下錨板抗拔承載力的研究并不合理，尤其是在錨板埋深比H/B比較大時，由于拉桿的影響，該模型試驗的試驗結果甚至與本文塊體集上限分析的理論預測趨勢相反。

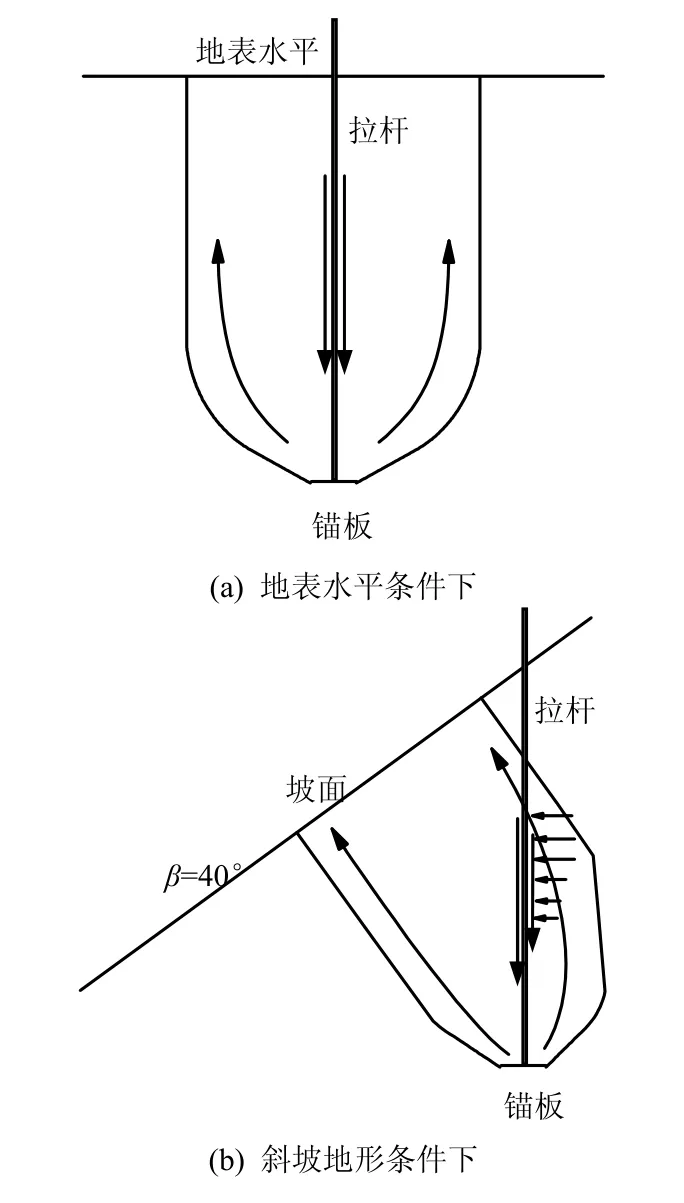
圖10 模型試驗中拉桿對錨板抗拔承載力的影響Fig.10 Effects of steel rod on pull-out capacity of anchor plates in laboratory test

鑒于此，對于斜坡地形條件下的淺埋錨板抗拔承載力研究，筆者認為應該盡可能采用從錨板底面施加推力的trapdoor模型，這樣就可以避免土體中拉桿的存在，而使得模型試驗結果能夠更好的反映錨板本身的抗拔承載力。

6 結 語

通過塊體集上限分析方法，本文研究了錨板的抗拔承載力和破壞面特性，并將分析結果與 Das[1]和Rowe[2]的錨板模型試驗結果進行詳細對比，驗證了塊體集上限法的有效性。然后運用塊體集上限法分析了考慮斜坡地形的Khing等[3]條形錨板抗拔承載力試驗，以及Rao和Prasad[4]的圓形錨板抗拔承載力試驗，通過與模型試驗結果的對比，分析了斜坡地形條件下模型試驗中采用拉桿加載的方式對于試驗結果的影響，并對錨板試驗模型的選取提出了合理的建議，（1）對于地表水平條件下，錨板模型試驗中拉桿的影響可以忽略，但是對于斜坡地形條件下，拉桿的影響不能忽略；（2）斜坡地形條件下，淺埋錨板的模型試驗應盡可能采用trapdoor模型。

[1]DAS B M. A procedure for estimation of ultimate uplift capacity of foundations in clay[J]. Soils and Foundations,1980,20(1): 77－82.

[2]ROWE R. Soil structure interaction analysis and its application to the prediction of anchor plate behaviour[D].Sydney，Australia: University of Sydney,1978.

[3]KHING K H,DAS B M,YEN S C. Uplift capacity of strip plate anchors in clay with sloping surface[C]//Proc.4th International Offshore and Polar Engineering Conference. Japan: International Society of Offshore and Polar Engineers,1994: 467－471.

[4]RAO S,PRASAD Y. Uplift capacity of plate anchors in sloped clayey ground[J]. Soils and Foundations,1992,32(4): 164－170.

[5]DICKIN E A. Uplift behavior of horizontal anchor plates in sand[J]. Journal of Geotechnical Engineering,1988,114(11): 1300－1317.

[6]DICKIN E A,LAMAN M. Uplift response of strip anchors in cohesionless soil[J]. Advances in Engineering Software,2007,38(8-9): 618－625.

[7]MURRAY E J,GEDDES J D. Uplift of anchor plates in sand[J]. Journal of Geotechnical Engineering,1987,113(3): 202－215.

[8]MURRAY E J,GEDDES J D. Resistance of passive inclined anchors in cohesionless medium[J]. Geotechnique,1989,39(3): 417－431.

[9]ROWE R,DAVIS E. Behaviour of anchor plates in sand[J]. Geotechnique,1982,32(1): 25－41.

[10]DAS B M,SEELEY G R. Breakout resistance of shallow horizontal anchors[J]. Journal of the Geotechnical Engineering Division,1975,101(9): 999－1003.

[11]ROWE R,DAVIS E. Behaviour of anchor plates in clay[J]. Geotechnique,1982,32(1): 9－23.

[12]劉明亮,朱珍德,劉金元. 錨板抗拉破壞機制試驗研究[J]. 巖土力學,2011,32(3): 697－708.LIU Ming-liang,ZHU Zhen-de,LIU Jin-yuan.Experimental study of failure mechanism of uplifting anchor[J]. Rock and Soil Mechanics,2011,32(3): 697－708.

[13]于龍,劉君,孔憲京. 錨板在正常固結黏土中的承載力[J]. 巖土力學,2007,28(7): 1427－1434.YU Long,LIU Jun,KONG Xian-jing. Stability of plate anchors in NC clay[J]. Rock and Soil Mechanics,2007,28(7): 1427－1434.

[14]GUNN M J. Limit analysis of undrained stability problems using a very small computer[C]//Proc.Symposium on Computer Applications to Geotechnical Problems in Highway Engineering. England: Cambridge University，1980: 5－30.

[15]余生兵,黃茂松. 基于組合塊體集的淺埋條形錨板上限分析[J]. 巖石力學與工程學報,2011,30(5): 1049－1056.YU Sheng-bing,HUANG Mao-song. Upper bound analysis of horizontally embedded anchors based on block set mechanism[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(5): 1049－1056.

[16]MERIFIELD R S,LYAMIN A V,SLOAN S W,et al.Three-dimensional lower bound solutions for stability of plate anchors in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering,2003,129(3): 243－253.