位置基準的分布對GPS 網優化設計的影響分析

劉明輝

0 引言

控制網的優化設計問題在測量界一直是一個經典的研究課題。GPS網的優化設計是實施GPS測量的基礎工作，它是技術設計所需達到的合理程度的一種狀態描述[1］。經典的設計理論未顧及到建網的費用指標，并不能算得上是真正的最優化網。因此，所謂的最優網，應該是在能夠滿足用戶對網的精度、可靠性要求的基礎上，盡量使用較低成本的控制網。

現如今，用戶對測繪成果的需求已經不僅僅只停留在高質量層面上，同時還要求消耗低成本。因此，如何在保證適當的質量控制指標的同時，將消耗成本降到最低，提高項目的效益，進行全面綜合的控制網優化設計，是一個值得研究的課題。

1 GPS控制網的數據處理

GPS網的數據處理大體可劃分為數據采集、數據傳輸、格式轉換、數據預處理、基線解算和網平差幾個階段[2］。

1.1 數據預處理

基線解算需要的是“干凈”觀測值，這就需要將存儲在計算機中的觀測數據進行預處理。這個階段主要包括數據格式轉換、數據篩選和編輯、數據標準化、接收機鐘差估算、線性組合觀測值形成、基線向量近似值估算和周跳探測、修復等。

1.2 基線解算

基線解算采用美國麻省理工學院(MIT)和斯克里普斯海洋研究所(SIO)研制的GPS數據后處理和分析軟件GAMIT，它是全球應用最廣泛的高精度GPS基線解算軟件之一，采用雙差載波相位模型解算，多安裝于Linux操作系統[3］。

1.3 GPS 網平差

GPS基線解算所得到的是基線向量，僅能確定點之間的相對坐標，要得到待定點的絕對坐標，就需要引入起算數據進行平差。GPS網平差的步驟分為以下幾個:提取基線向量，構建GPS網;進行無約束網平差;約束平差或者聯合平差;質量評定。本文中平差處理所用的軟件為武漢大學的COSA軟件。

2 GPS控制網優化設計的分類及指標

2.1 GPS控制網優化設計的分類

目前，廣泛應用的GPS控制網優化設計由Grafarend E.提出，主要包括以下四類[4］:

零類優化設計是指在明確了網平差模型的系數矩陣和權陣的條件下，求解未知數協因數陣的過程。

一類優化設計是在全網觀測點數和基線數大概確定之后，通過對網形的設計求出系數矩陣，以使得未知參數的協因數陣達到規定的精度要求。針對圖形矩陣的設計，如下一些因素可能會對平差精度有影響:點位移動、異步環的數量和網平差中基線向量的選取等。

二類優化設計，是在已確定網形，即已知平差模型的系數陣和未知數協因數陣的基礎上，對權陣進行優化設計的過程。

三類優化設計，是指對于精度沒有達到要求的GPS網進行加密，使其逐漸滿足精度要求的過程。

測量實踐中，權陣和網形加密的情況不是很多，優化設計的主要工作集中在基準設計和網形設計這兩部分內容。

2.2 GPS控制網優化設計的指標

GPS控制網優化設計的數學模型為:

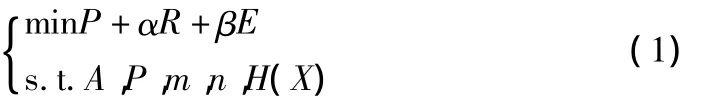
其中，P，R，E分別為精度、可靠性、經濟指標;α，β均為常數，它們的不同取值可調節以上三個指標之間的比例關系;s.t.表示“約束于”，分別為圖形矩陣和權矩陣;m，n分別為未知數的個數和觀測值的個數;H(X)為限制條件函數。優化設計的目的就是通過調整改變約束條件中各因素的比例關系，即對網的各種參數(如基準、圖形參數、觀測權參數等)進行設計，使得目標函數得到極小值。

3 位置基準的分布對GPS網精度的影響

在進行平差之前，GPS網是一個自由網，要想獲得待求參數的平差值，必須選取較高精度的點作為平差基準。對于大范圍和高精度的GPS數據處理，起算基準的選擇顯得十分重要，通常都選擇具有高精度的IGS地心坐標基準站。

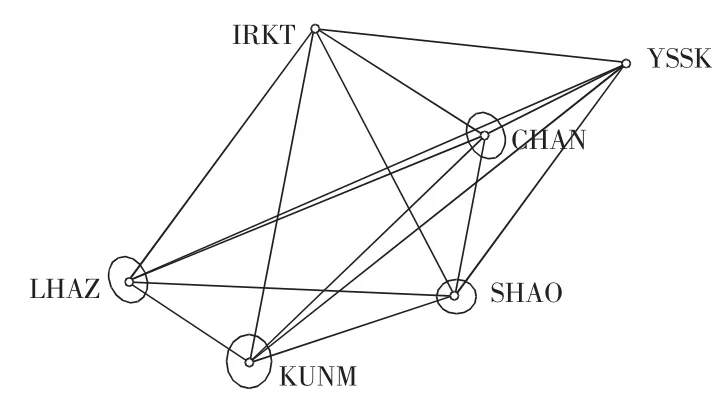
圖1 高緯度IGS基準站的GPS網形

下面通過實例來說明IGS基準站的分布對GPS網精度的影響。

設計兩個簡單的方案來分別說明高、低緯度基準站對GPS網精度的影響。選取中國境內的四個IGS站作為未知點，分別是CHAN，KUNM，LHAZ，SHAO。基準選取方案:方案一選取北半球的兩個高緯度基準站，它們是IRKT(B=52°)，YSSK(B=47°);方案二選取北半球的兩個低緯度基準站，它們是HYDE(B=17°)，GUAM(B=13°)。

相應網形圖分別見圖1，圖2。

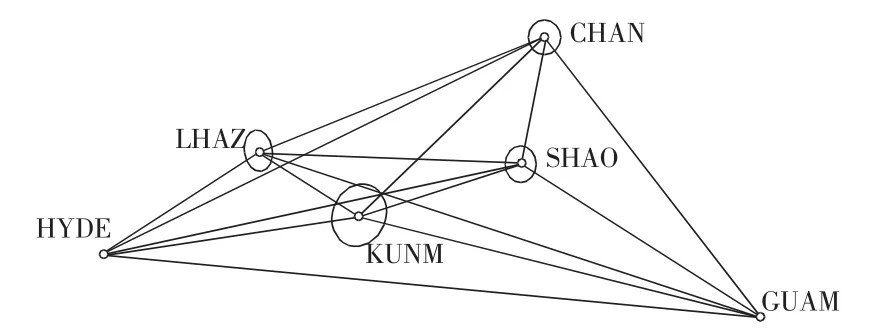
圖2 低緯度IGS基準站的GPS網形

利用GAMIT軟件進行基線解算之后，采用COSA軟件分別將兩組不同的基準站與中國境內的四個待求站 CHAN，KUNM，LHAZ，SHAO一起進行平差。解算結果顯示:與方案一相比，方案二在X，Y坐標分量上的平均精度分別提高35.6%和34.6%，在Z坐標分量上的平均精度提高47.6%。由此可得:在所選IGS基準站個數相等的情況下，選擇低緯度的基準站比選擇高緯度基準站的精度在各個坐標方向都要高，尤其表現在Z坐標上。

4 結語

選擇IGS站位置的不同，對GPS網精度的影響也不相同。在所選IGS站數量相同的時候，選擇低緯度的IGS站與選擇高緯度的IGS站相比，各個坐標軸的精度都有提高，尤其是Z軸。因此，在選擇基準站時，最好是結合全球IGS站的地理分布狀況，盡量選擇低緯度的站點[5］。

[1]李 輝.高精度GPS控制網的優化設計研究[D］.北京:北京交通大學碩士論文，2009.

[2]李征航，黃勁松.GPS測量與數據處理[M］.武漢:武漢大學出版社，2005.

[3]劉志廣，占 偉.Ubuntu系統平臺的 GAMIT/GLONK10.35安裝詳解[J］.全球定位系統，2009(5):32-34.

[4]晁定波，薄志鵬.現代大地控制網優化設計原理[M］.武漢:武漢測繪科技大學出版社，1991.

[5]隋立芬，許其鳳.GPS數據處理中IGS基準站的選取[J］.測繪學院學報，2003，20(1):124-126.