其實集合試題也可以很精彩
——品味近2年高考中的集合試題

●

(湖州中學 浙江湖州 313000)

其實集合試題也可以很精彩
——品味近2年高考中的集合試題

●馮耀斌

(湖州中學 浙江湖州 313000)

集合語言是現代數學的基本語言，是表達數學知識、進行數學交流的重要工具，因此集合知識在高考中倍受青睞，是每年高考中的必考內容．長期以來，不管是學生還是教師，都存在著這樣一個誤區：高考中集合一般就出現在選擇題第一題或者填空題第一題，且都是簡單題．而筆者通過分析近2年全國各地數學高考卷發現，其實只要給集合穿件新衣服，集合試題可以很難，當然也很精彩，值得細細品味(限于篇幅，本文僅選取典型的案例進行論述).

1 考查雙基，重視基本數學知識

元素與集合的關系和集合的運算是集合知識中最基礎的內容，考查此類知識的試題，往往對學生的基本數學思想和方法具有一定的要求,難度不大，只要掌握基本的集合概念、集合運算即可．

例1若集合A={x||x|≤1,x∈R}，B={y|y=x2,x∈R}，則A∩B=

( )

A.{x|-1≤x≤1} B.{x|x≥0}

C.{x|0≤x≤1} D.φ

(2010年江西省數學高考理科試題)

例2已知集合A={(x,y)|x,y為實數，且x2+y2=1},B={(x,y)|x,y為實數，且y=x},且B=A∩B的元素個數為

( )

A.0 B.1 C.2 D.3

(2011年廣東省數學高考理科試題)

例1和例2屬于基礎題，分析略．

答案：C；C．

2 考查思維，注重基本數學思想

求集合的(真)子集個數是歷年高考的常見題型．在平時教學時，強調集合A={a1,a2,…,an}有2n個子集，有2n-1個真子集，有2n-1個非空子集，有2n-2個非空真子集.而在實際應用時，往往不會直接套用上述公式，而是需要通過一定的分析，需要基本的數學思想，方能轉化為用公式求(真)子集的問題．

( )

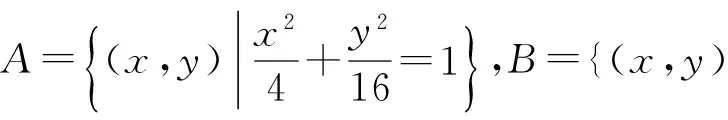
A.4 B.3 C.2 D.1

(2010年湖北省數學高考理科試題)

分析本題主要考查集合的子集個數及集合的簡單運算．

答案：A．

例4設集合A={1,2,3,4,5,6},B={4,5,6,7,8}，則滿足S?A且S∩B≠φ的集合S的個數是

( )

A．57 B．56 C．49 D．8

(2011年安徽省數學高考理科試題)

分析本題主要考查集合的關系與運算以及分類討論思想，題目難度屬中等．

答案：B．

3 知識整合，強調綜合應用

集合與函數、集合與不等式等內容的碰撞容易產生新的“火花”，題目從形式上看，要比單獨函數題、不等式題更加豐富更加飽滿．因此，高中數學各個章節內容的整合，不僅僅是知識點的簡單復合，更是各種知識體系的交匯，多種解題思想的交融，強調對知識技能的綜合應用．

例5設非空集合S={x|m≤x≤l}滿足：當x∈S時，有x2∈S．給出以下3個命題：

①若m=1，則S={1}；

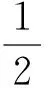
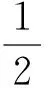
其中正確命題的個數是

( )

A．0 B．1 C．2 D．3

(2010年福建省數學高考文科試題)

答案：D．

例6設集合

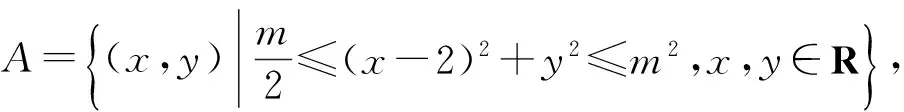
若A∩B≠φ，則實數m的取值范圍是________.

(2011年江蘇省數學高考試題)

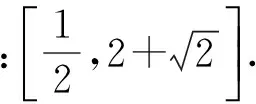
4 挖掘內涵，開闊解題思路

數學試題表面形式可以五花八門，但其本質還是比較明確的．集合的表達形式就有多種，借用集合的“新衣”來裝扮的試題種類就更多了：或用集合來表達點、線、面，或用集合來表達數、函數、方程，但究其本質，跳不出“數”和“形”這2個方面.2010年和2011年浙江省數學高考理科的最后一道選擇題分別很好地詮釋了如何用“形”和“數”的視角來解決集合問題．

例7設a,b,c為實數，

f(x)=(x+a)(x2+bx+c)，

g(x)=(ax+1)(cx2+bx+1)，

記集合

S={x|f(x)=0,x∈R}，T={x|g(x)=0,x∈R}．

若|S|，|T|分別為集合元素S，T的元素個數，則下列結論不可能的是

( )

A.|S|=1且|T|=0

B.|S|=1且|T|=1

C.|S|=2且|T|=2

D.|S|=2且|T|=3

(2011年浙江省數學高考理科試題)

分析本題的內涵是結合集合的知識特別是集合元素個數的新素材考查了函數零點及零點個數的概念，難度較大．

取a=0，b=0,c=0,則

S={x|f(x)=x3=0}，|S|=1，

T={x|g(x)=1=0}，|T|=0，

因此選項A可能成立．

取a=1,b=0，c=1,則

S={x|f(x)=(x+1)(x2+1)=0}，|S|=1，

T={x|g(x)=(x+1)(x2+1)=0}，|T|=1，

因此選項B可能成立．

取a=-1，b=0,c=0,則

S={x|f(x)=(x-1)x2=0}，|S|=2，

T={x|g(x)=(-x+1)(-x2+1)=0}，|T|=2，

因此選項C可能成立．

答案：D．

5 閱讀理解，培養信息分析能力

“數學素質是公民文化素質的重要組成部分”．閱讀理解能力作為數學素質的有機組成部分，在近幾年的全國高考中表現得尤為突出．集合以其特殊的地位成為此類蘊含大量新信息創新題的首選.筆者認為，集合的特殊性由集合論本身的高度抽象、廣度范疇，與高中數學集合涉及部分的淺、窄共同作用而形成，以致對集合稍微加點新定義、新知識、新法則，就能在高中數學與高等數學之間的“空白”處綻放出燦爛的光芒．解決這類題目的關鍵是準確獲取新信息，并分析使之轉化為與所掌握知識相關聯的信息．

例8設S為復數集C的非空子集.若對任意x,y∈S，都有x+y，x-y，xy∈S，則稱S為封閉集．下列命題：

①集合S={a+bi|a,b為整數，i為虛數單位}為封閉集；

②若S為封閉集，則一定有0∈S；

③封閉集一定是無限集；

④若S為封閉集，則滿足S?T?C的任意集合也是封閉集.

其中真命題是________(寫出所有真命題的序號)

(2010年四川省數學高考理科試題)

分析直接驗證可知①正確.

當S為封閉集時，因為x-y∈S，取x=y，得0∈S，②正確.

對于集合S={0}，顯然滿足所有條件，但S是有限集,③錯誤.

取S={0}，T={0,1}，滿足S?T?C,但由于0-1=-1?T，故T不是封閉集，④錯誤.

答案：①②.

例9設S是整數集Z的非空子集，如果任意a,b∈S，有ab∈S，則稱S關于數的乘法是封閉的．若T,V是Z的2個不相交的非空子集，T∪V=Z，且任意a,b,c∈T，有abc∈T；任意x,y,z∈V，有xyz∈V，則下列結論恒成立的是

( )

A.T,V中至少有1個關于乘法是封閉的

B.T,V中至多有1個關于乘法是封閉的

C.T,V中有且只有1個關于乘法是封閉的

D.T,V中每一個關于乘法都是封閉的

(2011年廣東省數學高考理科試題)

分析本題考查對新定義集合概念的理解，考查角度新穎，主要考查學生的閱讀理解能力和知識遷移能力，難度較大．

答案：A．

6 拓展抽象能力，優化解題策略

提高學生思維能力是國家新課程標準的基本要求，新課程標準重視培養學生的思想品質．因此近2年高考試題構思巧妙，設計新穎，目的是增大考生的抽象思維空間、歸納思維品質及優化解題策略，試題穩中有變、變中求新，始終體現對學生數學解題能力和素養的考查．下面2個例題以集合題目為載體，頗具代表性，高度抽象，同時知識遷移后對解題策略的選擇有一定的指導價值．

例10若規定E={a1，a2，…，a10}的子集{ak1，ak2，…，akn}為E的第k個子集，其中k=2k1-1+2k2-1+…+2kn-1，則

(1){a1,a3}是E的第________個子集；

(2)E的第211個子集是________．

(2010年湖南省數學高考文科試題)

分析(1)由所給的定義知

k=21-1+23-1=5．

(2)方法1由題意要使得

k=211=2i1-1+2i2-1+…+2in-1，

可由211=128+64+16+2+1，然后求出相應的i1,i2,…，in．

方法2換種解題策略，此題本質是一個二進制問題，將211化為二進制數是11 010 011(2)，即

11 010 011(2)=27+26+24+21+20，

容易得到i1,i2,…,i5(i1

本題是抽象型新定義試題，構思新穎，亮點明確，主要考查學生在新情境下抽象分析問題、解決問題的能力．

( )

(2011年四川省數學高考理科試題)

分析本題除綜合考查了平面向量的數量積、平面向量的應用、排列組合知識之外，還考查了學生應用新知識抽象分析問題、解決問題的能力及邏輯思維能力，難度較大．

答案：B.

以上筆者通過近2年全國各地高考中集合試題出現的頻率及不同形式，以“集合”為點，闡述了同一章節內容通過不同知識的包裝、不同技能的拓展、不同思維的碰撞后，所產生的多樣性和復雜性．因此數學教學的根本任務，是要引導學生建構良好的數學認知結構，以滿足其后續學習的需要；教學過程應該重視對數學思想、方法的歸納提煉，認識和把握最本質的因素．