方腔流致振蕩及噪聲的數值研究

萬振華，周 林，孫德軍

（中國科學技術大學近代力學系，安徽 合肥230027）

0 引 言

一般認為長高比L／D＜6的方腔流動為開式流動，其在航空、航天以及其它工業領域應用廣泛，如起落架艙、武器艙、敞篷汽車等。開式方腔流動會產生強烈的振蕩，有可能引發結構疲勞損傷和噪聲污染。振蕩的誘因、幅值、抑制方法等都很值得研究，涉及流動失穩、波渦非線性作用、自持振蕩等許多理論問題。故20世紀50年代以來，方腔流致振蕩和發聲問題就已經引起了眾多研究者的興趣［1］。Krishnamurty［2］最早從實驗得到方腔聲場結構，Rossiter［3］總結了預測振蕩頻率的半經驗公式，Tam和Block［4］引入線性穩定性分析提出了新的頻率預測模型，Rowley等［1，5－6］對方腔的空間穩定性、降維模型、理論模型、控制等問題進行了一系列研究，Shieh［7］等對高Reynolds數下不同構型方腔進行了湍流數值模擬研究。衣云峰［8］研究了低亞聲速突出和陷落式圓柱空腔流動，并歸納了頻率公式。羅柏華等［9］實驗研究了純音激勵方式的噪聲抑制。此外，羅柏華［10］、侯中喜等［11］、李曉東等［12］等使用不同數值方法都成功模擬出了方腔流場的振蕩、聲波傳播性質。

雖然國內外研究內容已經很多，但仍然有很多問題有待深入研究，如目前對方腔的振蕩存在兩種認識［1，6］：一種認為它是自持的，另外一種認為它是輕微衰減的系統，所以具體振蕩性質需由實際情況具體分析。關于方腔振蕩的低頻成分也有幾種不同產生方式，如渦－后拐角撞擊方式變化導致低頻產生［13］，湍流間歇結構導致模態切換［14］引入低頻等。此外，目前對回流區與剪切層相互作用研究較少。

本文采用直接數值模擬方法，研究了低Reynolds數、亞聲速開式方腔流動的振蕩及噪聲問題，特別是回流區與剪切層相互作用及其與低頻的關系。首先，研究了來流邊界層厚度的影響，探討了所涉及參數范圍內的方腔流動振蕩機制；針對來流邊界層變薄后出現的低頻成分，從回流區與剪切層相互作用出發分析了其產生的機制。其次，采用本征正交分解（POD）方法，分析了回流區與剪切層相互作用對剪切層渦結構的影響，以及渦結構改變與渦－后拐角撞擊方式的關聯。最后，計算得到了方腔的聲場結構，通過脹量場的分析得到了聲波產生和傳播的過程。

1 數值方法

1.1 計算方法

采用直角坐標系下二維可壓縮Navier－Stokes方程：

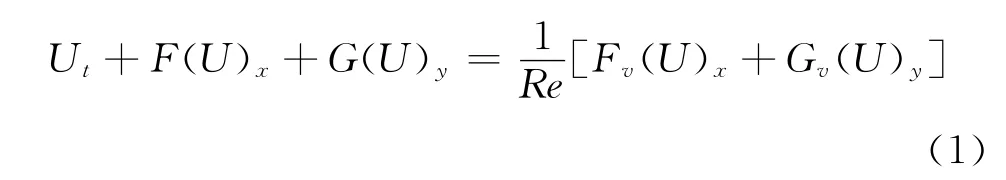
考慮到捕捉噪聲，所以空間使用了的6階緊致格式離散［15］，時間方向使用低耗散和低色散的Runge－Kutta格式［16］，粘性項使用的6階中心差分格式。方程以遠場聲速a∞進行無量綱化。Reynolds數定義為Re＝ρ∞a∞D／μ∞，取Prandtl數Pr＝0.72。粘性系數以Sutherland公式給出，其中遠場溫度T∞＝300K。

計算模型如圖1所示，方腔的高度定義為D，長度為L，方腔前端延伸到－6D，尾端延伸到13D，上端延伸到15D。邊界條件設定如下：方腔上部左、右端分別為無反射亞聲速出、入口，上方設定為無反射出口，固壁邊界設為等溫壁［17］。在方腔上部三個方向施加海綿層邊界條件［18］以抑制邊界反射。另外，采用了10階中心濾波抑制數值偽振蕩。初始條件給定如下：腔體上部以基本流速度型進行初始化；腔體內部速度設為0。密度和壓力設為遠場條件。

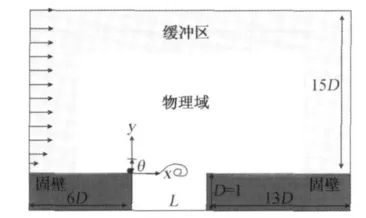
圖1 方腔設定與計算域的示意圖Fig.1 Schematic diagram of cavity configuration and computational domain

1.2 計算參數選擇

本文主要研究高亞聲速低Reynolds數（相對于湍流發生的Reynolds數）方腔流動振蕩和發聲問題。選擇典型的方腔長高比為L／D＝2，Re＝2500，同時也便于和已有實驗結果進行比對。來流為層流狀態，研究了不同來流馬赫數M、來流邊界層動量厚度θ的影響，具體計算參數如表1所示。

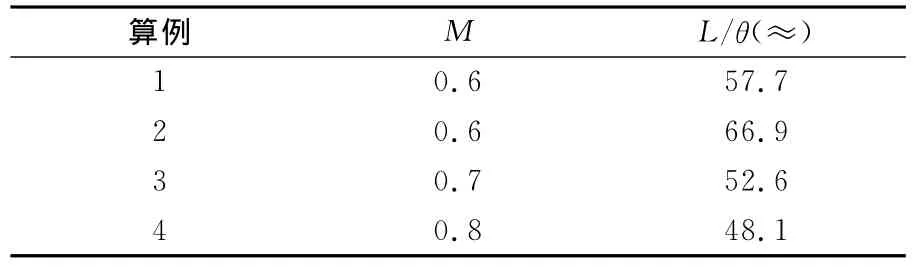
表1 算例列表Table 1 Computational cases

1.3 網格收斂性驗證

本文使用的程序由文獻［19－20］中程序發展而來，涉及的空間格式、邊界條件等均已很好驗證，如采用本文中的數值算法計算文中［21］的Taylor－Green渦算例，條件設定與文獻［21］相同，在13×13的網格上求解得到了Taylor－Green渦速度隨時間的衰減（如圖2），無量綱時間t＝1／（8π2）時的計算解與理論解的相對誤差小于0.03%。考慮到聲學問題對網格分辨率要求很高，所以為了確保文中使用的網格滿足要求，本文做了網格收斂性分析。計算采用單向拉伸網格，針對L／D＝2的情形，文中使用的計算網格為：腔外網格為918×416，腔內網格為262×118，總網格點數約為40萬，與文獻［5］網格數相當，網格在固壁附近和唇口處最密，唇口兩端靠近壁面（x方向）的網格間距Δx／D≈0.005，在－0.1＜y／D＜0.1區間內集中了32層網格，最小的網格間距Δy／D≈0.005。再考慮一套加密的網格：腔外網格為1118×510，腔內網格為308×152，總網格點數約為60萬。比較算例1在兩套網格下后拐角位置的密度隨時間的變化。如圖3（a）所示，二套網格下密度的變化基本相同，相應峰值差別很小，且相位基本保持同步。為了更精確地比較頻譜誤差，圖3（b）給出了前200個無量綱時間密度的FFT變換后在譜空間上幅值。從圖中可以看出在各種頻率下，二者幅值相差很小，如在主頻f＝0.216上幅值的誤差小于1×10－3，故說明當前選擇的計算網格密度已經足夠。

圖2 Taylor－Green渦的速度隨時間衰減Fig.2 The decaying of velocity for a Taylor－Green vortex

圖3 網格收斂性驗證Fig.3 Validation of mesh convergence

2 計算結果及討論

2.1 流場的振蕩現象

目前，對方腔流場振蕩機制的認識存在兩種觀點。一種觀點認為，振蕩是自持的：腔體內外流體的剪切誘導Kelvin－Helmholtz不穩定性，產生渦卷起；渦卷起后向下游運動，進而與后拐角撞擊壓縮產生往前傳的聲波；聲波到達方腔前端會再次激發剪切層失穩，使新渦卷起，完成自持振蕩過程。所以，在無任何外部持續激勵時，方腔流動仍會持續地振蕩。此時方腔流動的動力學系統可認為是一個關于不穩定平衡點（Navier－Stokes方程定常解）的穩定的極限環［5－6］，振蕩的幅值取決于非線性效應，如剪切層失穩中擾動增長達到飽和。還有一種觀點認為，方腔流動是穩定的、輕微衰減的系統，只有在外界持續激勵下（如邊界層內湍流脈動，壁面粗糙引起擾動等）才能維持振蕩［1，6］；撤除激勵，振蕩現象也將消失。

本文的計算中沒有施加任何外部激勵，在所計算的參數范圍內得到了流場的振蕩現象，計算結果支持第一種觀點，即屬于自持振蕩。振蕩的強弱可以采用聲壓級來表征（圖4），結果表明，邊界層動量厚度θ越小，則方腔底部聲壓級越高，即振蕩幅值越大。這與剪切層的不穩定性特性相吻合，即剪切層θ減小導致擾動的空間增長率增加。所以，振蕩幅值與θ的變化關系主要與剪切層的空間不穩定性增長率有關，這種剪切層的對流不穩定性與下游方腔中的反饋機制相結合，仍然可以形成自持的振蕩，而無需來自外界持續擾動的激勵。

Rossiter［3］于1964年提出了預測振蕩頻率的半經驗公式，其形式如下：

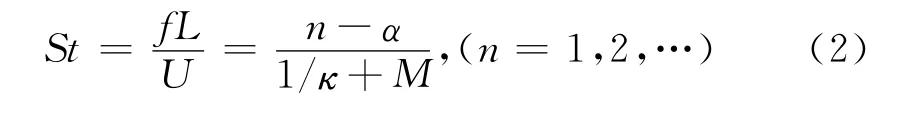
圖4 方腔底部的聲壓級（M＝0.6）Fig.4 Sound pressure levels of cavity floor at M＝0.6

其中，κ＝0.57是一個經驗常數，α＝0.25為渦撞擊后拐角到產生聲波的相位滯后，n為剪切層中渦的數目，對應模態的階數。n＝1，2的模態分別稱為Rossiter I、II模態。圖5給出了不同馬赫數下得到的振蕩頻率，在本文的計算參數范圍內只得到了Rossiter II模態，這與Krishnamurty［2］的實驗結果是基本符合的。本文的頻率與文獻［5］中Rossiter II模態的頻率接近，但都略低于實驗［2］得到的頻率，原因可能是實驗中的Reynolds數更高和來流邊界層厚度不同造成的。此外，實驗中同一馬赫數下出現多個頻率，這可能是由于來流邊界層厚度不同造成的頻率偏移。在本文中這種偏移很小，而在湍流模擬中這種頻率偏移現象明顯［12］，原因可能是湍流情況下頻率不再是明確的大尺度渦結構對流主導，導致對邊界層厚度改變更加敏感。

圖5 不同馬赫數下的振蕩頻率Fig.5 The oscillation frequencies at different Mach numbers

當M＝0.6，由圖6（a）和圖6（c）中的相圖可知，算例1的振蕩是周期的；隨著來流邊界層厚度的減小，算例2則為準周期的。相應地，從圖6（b）和圖6（d）可以看出，算例1中只存在對應Rossiter II模態的單一頻率St＝0.72；而算例2中存在兩個頻率，St1＝0.72的基頻能譜占主導地位，仍和Rossiter II模態一致，但同時出現了低頻成分St2＝0.36，視為亞諧頻。雖然亞諧頻非常靠近Rossiter I模態的頻率，但其不符合Rossiter關于I模態中只有單渦的定義，故我們認為這個低頻不是I模態。它的產生與Rockwell等的實驗結果［13］相似，Rockwell等認為這是因剪切層中渦－后拐角撞擊方式變化造成的。Rockwell的實驗［13］是在水洞中進行的，本文計算的低Reynolds數、高亞音速情況的氣體流動，結果表明，渦－后拐角撞擊不穩定仍然存在，它們是回流區與剪切層相互作用形式不穩定的結果。

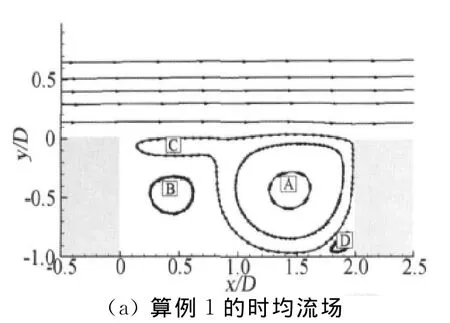
圖7（a）給出了算例1的時均流場結構，從圖中可以清晰地區分幾個主要區域：主回流區A，A區誘導的主反向流動區域B，次回流區C，A區誘導的次

反向流動區D。回流區流動可以改變剪切層中渦心軌跡和橫向運動速度。圖7（b）為渦心運動軌跡，可以將其大致分為4個區域：I區為自由發展區，渦心橫向運動速度以及縱向位置沒有改變。II區渦受次回流區C后端牽引運動方向會向方腔內偏斜，同時由于越靠近方腔橫向對流速度越小，渦橫向運動速度會減小。III區渦進入主回流區，渦會被主回流區A前端牽引上升，上升越高橫向對流速度越大，渦的橫向運動速度越快。IV區渦受A后端牽引位置逐漸下降，渦橫向運動速度減小。算例1中的剪切層渦都經過上述4個區域，最終與后拐角發生穩定的撞擊，即每次渦－后拐角的撞擊方式都相同，如圖7（c）所示，整個流場也呈Rossiter II模態形式的周期性振蕩，振蕩周期由相鄰兩次渦－后拐角撞擊的時間間隔決定。

圖6 （1.9D，0）位置的相圖與功率譜Fig.6 The phase diagram and power spectrum of perturbed pressure at the location（1.9D，0）

當來流邊界層厚度減小（算例2），由于剪切層的不穩定性增強，剪切層與腔內回流區的相互作用也明顯增強，導致剪切層渦呈高低交替出現，它們分別走過高、低兩條軌跡，每條軌跡也可大致分成上述的4個區域，如圖7（d）。由于此時的流動是準周期的，故各個周期內渦的運動軌跡還有細微的差異，但都接近于圖7（d）所示的高、低渦運動軌跡。

剪切層也可以通過渦量輸運的方式改變回流區的運動。現仍結合算例2進行分析。如果剪切層中前一個渦走低軌道，那么它將與后拐角發生圖7（e）形式的撞擊，其特點是撞擊后大部分渦量進入回流區，使得主回流相對變強，此即Rockwell等［13］實驗中的PC（Partial Clipping）形式的撞擊；主回流的加劇會使得剪切層中下一個渦走高軌道，它與后拐角將發生圖7（f）形式的撞擊，其特點是撞擊后只有少量渦量進入回流區，主回流相對變弱，此即Rockwell等［13］實驗中的PE（Partial Escaping）形式的撞擊，主回流減弱導致下一個渦將走低軌道。如此周而復始，形成準周期流動。由于此時兩次相鄰渦的撞擊不再是周期的，只有完成了一個PC到PE形式渦－后拐角撞擊過程才構成一個主周期，所以，這種撞擊方式的切換導致了新的低頻（亞諧頻）成分的產生。相對應的是，算例1中的渦撞擊形式介于PC與PE之間，且每次都相同，形成周期性流動，因此沒有低頻成分出現。

值得指出的是，前述Rossiter頻率預測公式（式2）是假設恒定的剪切層渦對流速度得到的，而回流區與剪切層的相互作用會改變渦橫向運動速度，會影響Rossiter公式的準確性。

算例3和算例4的結果類似，當來流邊界層較厚時，是沒有低頻的Rossiter II模態周期性流動，當來流邊界層變薄，會有低頻成分出現，不再贅述。

2.2 本征正交分解（POD）分析

為了進一步明晰回流區與剪切層相互作用對渦模態的影響，采用了等熵可壓縮的POD方法［22］進行了分析。由表2可知，算例2的能譜比算例1更寬，表明薄來流邊界層的相互作用更強。算例1中前兩個模態就捕捉了超過90%的能量，算例2中大部分能量需要前4個模態才能捕捉。算例1中的模態1和2的動力學結構基本類似，故圖8只給出了模態1和3。算例2中模態1和2，模態3和4的結構類似，因此圖9中只給出了模態1、3和5。可以看出，低階模態中，剪切層中均存在2個大渦結構，對應于功率譜中Rossiter II模態，故低頻成分不對應于Rossiter I模態。圖8（b）和圖9（c）中渦數目增多，渦結構變小，對應于功率譜中高頻成分，但能量很小。圖8（a）和圖9（a）的渦結構類似，渦縱向結構比較寬，這種渦結構傾向于PC形式的撞擊，圖9（b）中的渦結構則不同，比較扁平，更容易形成PE形式的撞擊。比較圖8和圖9還可以看出，算例2主回流區中渦結構要比算例1的更加復雜和紊亂。總體而言，POD模態驗證了低頻成分不是Rossiter I模態，回流區與剪切層的相互作用會影響渦結構的形態，從而改變渦－后拐角的撞擊方式。

圖8 算例1的POD模態的渦量場ω∈（－5，5）Fig.8 Vorticity filed of different POD modes for Case 1

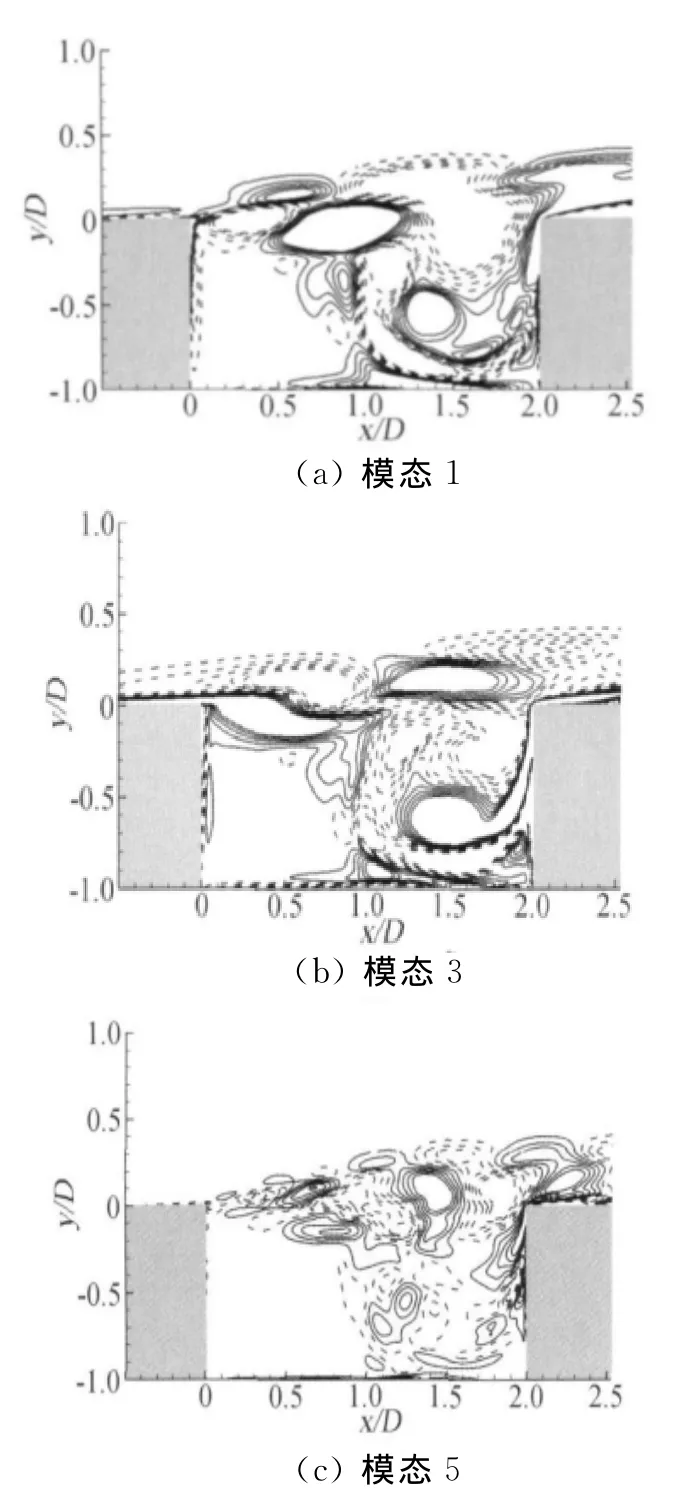
圖9 算例2的POD模態的渦量場ω∈（－5，5）Fig.9 Vorticity field of different POD modes for case 2

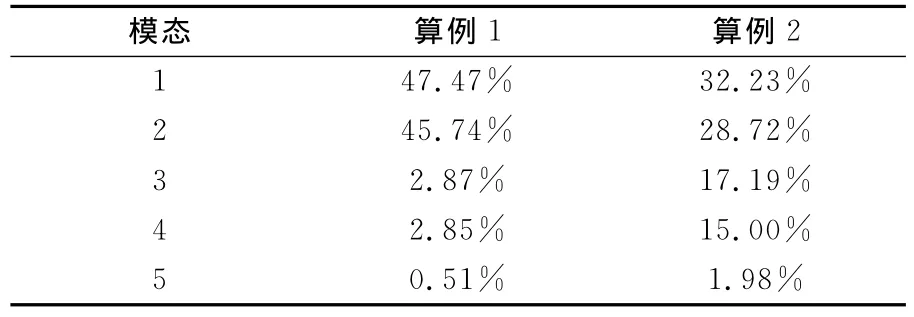
表2 能量分數Table 2 Energy fractions

2.3 聲波結構對比及分析

本文中的聲波結構通過脹量場和密度梯度兩種方式分別進行了表征。圖10（a）～圖10（c）為Krishnamurty［2］的實驗結果，聲場由密度的紋影圖給出。圖11（a）～圖11（c）為本文DNS模擬得到的結果。實驗與計算均使用層流來流邊界層，且都是被Rossiter II模態主導，所不同的是實驗的Reynolds數高出一個量級。由二者結果比較可知，雖然計算中Reynolds數較低，但二者聲場的定性結構，相位關系都基本相符。此外，從實驗和計算的結果均可看出，隨著馬赫數的增加，方腔外聲波的傳播方向會發生明顯變化，且兩道聲波之間相位差會變大，這些差別主要來自于聲波傳播過程中的對流效應，波陣面的形態取決于波速和當地流動速度的疊加（見圖12）。故在M＝0.6時，聲波傳播方向與流動夾角約為135°角，隨著馬赫數增加這個夾角逐漸減小。

圖12描述了聲波產生和傳播的具體過程：首先，渦－后拐角的作用產生聲波，聲波分別在腔外和腔內傳播（表示為波陣面I和II）。其次，因腔內對流速度較小，波陣面II傳播快于I，二者產生相位差。再次，腔內的波陣面II到達前壁面，部分透過剪切層輻射出方腔，剩下部分發生反射。最后，可觀察到腔外有兩道聲波I、II，腔內有II的反射聲波。聲波I、II在腔外相位差大小被腔體內外的對流速度的差異決定，故在算例1中聲波I、II相位差較小，而在算例4中聲波I、II相位差明顯。圖13以脹量場的形式給出了算例4中聲波傳播的具體過程，進一步驗證了圖12的描述的過程。值得注意的是，本文的計算很好地驗證了Tam等人［4］在理論建模時關于聲波傳播的描述，不同是計算中未能看到明顯的聲波II在腔體下壁面的反射聲波，可能原因是反射聲波相對其它聲波強度較弱，在旋渦中又易耗散，造成計算中不容易捕獲。

圖12 波陣面傳播過程示意圖Fig.12 Sketch of propagation of wave fronts

圖13 算例4的4個不同時刻的脹量場Fig.13 4snapshots of dilatation field for case 4

3 結 論

本文采用直接數值模擬方法，研究了低Reyn－olds數下L／D＝2的方腔的亞聲速流致振蕩現象及其誘導的噪聲。在所計算的參數范圍內，方腔流場的振蕩是自持的，并且由Rossiter II模態主導。振蕩幅值、頻率與來流邊界層厚度密切相關，當來流邊界層變薄，振蕩幅值增大，周期振蕩會轉變為準周期振蕩，并產生低頻成分。低頻成分產生的根本原因是回流區與剪切層的相互作用。這種相互作用會改變剪切層渦的結構、運動軌跡及速度，進而導致了不同的渦與后拐角撞擊方式；而撞擊方式的切換構成了低頻成分。采用本征正交分解（POD）方法，分析了不同振蕩形式所對應的本征模態渦結構。對于沒有低頻成分的周期振蕩情況，只發現一種能量集中的本征模態；而對于出現低頻成分的準周期振蕩情況，發現了兩種能量較為集中的本征模態，它們反映了回流區與剪切層相互作用對渦結構的影響，并與后拐角的不同撞擊方式有關。聲場的計算表明，渦－后拐角的撞擊作用會產生聲波，并分別在腔外和腔內傳播，形成兩個波陣面，它們之間的相位差與對流效應有關。

［1］ROWLEY C W，WILLIAMS D R.Dynamics and control of high－Reynolds－number flow over open cavities［J］.AnnualReviewFluidMechanics，2006，38：251－276.

［2］KRISHNAMURTY K.Sound radiation from surface cutouts in high speed flow［D］.California Institute of Technology，1956.

［3］ROSSITER J E.Wind－tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds［R］.Aeronautical Research Council Reports and Memoranda，Technical Reports 3438，1964.

［4］TAM C K W，BLOCK P J W.On the tones and pressure oscillations induced by flow over rectangular cavities［J］.JournalofFluidMechanics，1978，89（2）：373－399.

［5］ROWLEY C W，COLONIUS T，BASU A J.On self－sustained oscillations in two－dimensional compressible flow over rectangular cavities［J］.JournalofFluidMechanics，2002，455：315－346.

［6］ROWLEY C W，WILLIAMS D R，COLONIUS T，et al.Linear models for control of cavity flow oscillations［J］.JournalofFluidMechanics，2006，547：317－330.

［7］SHIEH C M.Parallel numerical simulations of subsonic，turbulent，flow－induced noise from two－and threedimensional cavities［D］.Pennsylvania State University，2000.

［8］衣云峰，何祚鏞.圓柱形腔流激振蕩及其耦合共振的研究［J］.聲學學報，1996，21（4）：339－456.

［9］羅柏華，胡章偉.流動誘導空腔振蕩及聲激勵抑制的實驗研究［J］.南京航空航天大學學報，1996，28（3）：331－336.

［10］羅柏華.二維高亞音速空腔流激振振蕩的數值模擬研究［J］.空氣動力學學報，2002，20（1）：84－88.

［11］侯中喜，易仕和，王承堯.超聲速開始空腔流動的數值模擬［J］.推進技術，2001，22（5）：400－403.

［12］李曉東，劉靖東，高軍輝.空腔流激振發聲的數值模擬研究［J］.力學學報，2006，38（5）：599－604.

［13］ROCKWELL D，KNISELY C.Vortex－edge interaction：mechanisms for generating low frequency components［J］.PhysicsofFluids，1980，23（2）：239－240.

［14］GLOERFELT C，BOGEY C，BAILLY C.Numerical evidence of mode switching in the flow－induced oscillations by a cavity ［J］.InternationalJournalof Aeroacoustics，2003，2（2）：193－218.

［15］COLONIUS T，LELE S，MOIN P.Sound generation in a mixing layer［J］.JournalofFluidMechanics，1997，330：375－409.

［16］BERLAND J，BOGEY C，BAILLY C.Low－dissipation and low－dispersion fourth－order Runge－Kutta algorithm［J］.ComputersandFluids，2006，35：1459－1463.

［17］POINSOT T J，LELE S.Boundary treatment for direct simulations of compressible viscous flows［J］.Journal ofComputationalPhysics，1992，101：104－129.

［18］FREUND J B.Proposed inflow／outflow boundary conditions for direct computation of aerodynamic sound［J］.AIAAJ.，1997，25（4）：740－742.

［19］WEI M J.Jet noise control by adjoint－based optimization［D］.University of Illinois at Urbana－Champaign，2004.

［20］周林，萬振華，魏明駿，等.亞聲速時間混合層的噪聲研究［A］.第十三屆全國分離流、旋渦和流動控制會議論文［C］，2010：220－224.

［21］REMBOLD B.Direct and large－eddy simulation of compressible rectangular jet flow［D］.Swiss Federal Institute of technology，2003.

［22］ROWELY C W，COLONIUS T，MURRAY R M.Model reduction for compressible flows using POD and Galerkin projection［J］.Physcia.D.，2004，189：115－129.