艦船高傳遞損失復合托板振動特性優(yōu)化設計

姚熊亮 邱中輝 龐福振 謝曉忠

哈爾濱工程大學船舶工程學院，黑龍江哈爾濱 150001

0 引 言

將潛艇的典型艙段簡化為有限長加筋雙層圓柱殼結構，內層耐壓殼體與外層非耐壓殼體依靠托板和實肋板等舷間橫向構件來保證剛度。設備激勵由聯(lián)接基座引起耐壓殼體振動，通過舷間橫向連接構件將振動波傳遞給非耐壓殼體，內、外殼間的耦合作用很強，向水中輻射噪聲較大。在舷間主傳遞途徑中，可對振動波進行有效阻隔，以減弱內、外殼的耦合作用，由此，非耐壓殼體的振動級和水中輻射聲壓級將會降低［1］。由于托板結構是舷間振動的主要傳遞介質，其既能保證水下結構的強度，又能有效降低水下結構的輻射噪聲，因此，研究具有阻抑振動波傳遞的托板結構形式具有重要的工程價值。在潛艇舷間托板結構上布設剛性阻振質量來阻抑能量的傳遞，其隔振效果較明顯［2］。由于阻振質量是實體結構，相對板結構而言具有大的阻抗，致使抵達阻振質量塊的振動波部分被反射，從而會減少到達外層殼體的能量［3］。對于將剛性阻振質量布置在基座上的對結構振動進行優(yōu)化的情況，筆者已進行過相關研究［4］。但由于在托板結構上焊接剛性阻振質量塊的工藝復雜，焊接質量塊會使原艙段增加的重量較多，因此，剛性阻振質量在復合托板中的實際應用往往會受到限制。而將剛性阻振質量用等截面慣性矩的型鋼代替，則既能方便工藝，又便于取材。同時，在托板上開孔既可減少艙段重量，而且還可充分利用潛艇舷間橫向連接結構的不連續(xù)性來阻隔振動波的傳遞［5］。

本文將引入結構動力學優(yōu)化設計理論，探索艦船高傳遞損失復合托板的設計理論和方法，在滿足艙段總重量及強度約束的限制條件下，建立高傳遞損失托板的優(yōu)化設計模型，并進行以開孔半徑及托板角度為設計變量，以艙段非耐壓殼體全頻域內的平均振動加速度級為目標函數(shù)的動力學優(yōu)化設計，所得最優(yōu)參數(shù)的減振效果的托板可為實艇的減振降噪設計提供一定的參考。

1 艦船高傳遞損失復合托板優(yōu)化模型描述

由于球扁鋼的參數(shù)不能直接進行優(yōu)化，因此，優(yōu)化設計首先以艦船托板中阻振質量的截面尺寸及布設位置為設計變量，采用參數(shù)化定義、參數(shù)化建模、求解、結果提取、優(yōu)化變量（設計變量、狀態(tài)變量、目標函數(shù)）來賦值，其目的是在滿足艦船艙段總重量的限制約束條件下，使非耐壓殼體的平均振動加速度級最小，具體優(yōu)化分析流程圖如圖1所示。然后，再將優(yōu)化后的剛性阻振質量復合托板等效為高傳遞損失復合托板［6］。

本文采用的潛艇艙段模型為內、外殼有環(huán)肋加強的雙層圓柱殼體，其具體幾何尺寸為：艙段圓柱部分長度l1=8.4m，外徑D=8.6m，內徑d=7m，采用內、外環(huán)肋加強，肋距l(xiāng)=0.6m，托板厚度t1=0.008m，外殼板厚度t2=0.012m，內殼板厚度t3=0.028m，在內殼結構底板上對稱布置基座，剛性阻振質量托板結構如圖2所示。高傳遞損失復合托板艙段模型如圖3所示。

圖1 優(yōu)化分析流程圖Fig.1 Flow chart of optimization design

圖2 剛性阻振質量復合托板舷間結構正視圖Fig.2 Front view of composite pedestal with rigid vibration isolation mass

圖3 高傳遞損失復合托板艙段模型示意圖Fig.3 Scheme of submarine typical double cylinder shell

連接耐壓殼體與非耐壓殼體的托板和實肋板是雙層圓柱殼體舷間傳遞振動噪聲的主要途徑，舷間結構如圖4所示。所謂艦船高傳遞損失復合托板，即在托板結構中靠近內殼的一側布置具有隔振作用的、等效于剛性阻振質量塊的球扁鋼，并充分利用結構的不連續(xù)性，以在托板上開孔來阻抑振動波向非耐壓殼體及外流場的傳遞，從而達到減振降噪的目的［7］。阻振質量塊截面中心與艙段耐壓殼體的距離為e，截面尺寸為a×b，其中a為軸向尺寸，b為徑向尺寸。模型參數(shù)需要通過變量用參數(shù)化來實現(xiàn)。整個艙段優(yōu)化模型的材料參數(shù)為：彈性模量 E=210000MPa，泊松比μ=0.3，密度 ρ=7800kg/m3。

圖4 高傳遞損失復合托板舷間結構Fig.4 Composite pedestal connecting structures with high transmission loss between double shells

將設備運轉的簡諧激擾力作用在基座面板上，進行在頻域內的諧響應動力學優(yōu)化分析。將艙段沿縱向方向前、后各延伸3個肋位，以模擬實際潛艇臨近艙段的邊界條件影響，在邊界處，沿周向施加位移的全約束。將設備重量以質量點的形式均布于基座面板上，在基座面板上施加諧響應的設備激勵力，激勵頻率為在0～1000Hz頻段內的倍頻程［8］。

2 高傳遞損失復合托板結構形式優(yōu)化分析

首先，在托板上布設剛性阻振質量塊，通過優(yōu)化分析得到最優(yōu)的剛性阻振質量截面尺寸及布置位置。由于在托板結構上焊接剛性阻振質量塊工藝復雜，使原艙段增加重量較多，因而使得剛性阻振質量的實際應用效果有所下降。將復合托板中的剛性阻振質量用等效截面慣性矩的型鋼來代替，并通過開孔，充分利用潛艇舷間橫向連接結構的不連續(xù)性來阻隔振動波在舷間的傳遞，以達到減振降噪的目的。

先通過對剛性阻振質量塊截面尺寸及布置位置進行優(yōu)化，得到最優(yōu)的布置位置在距離艙段耐壓殼體2c1(D-d)=0.42處，最優(yōu)的截面尺寸為a=0.074 m，b=0.043 m。將其等效為球扁鋼，新增的骨材會導致艙段模型的重量增加，這可通過開孔和改變托板夾角來減輕重量。如圖5所示，最終確定的托板結構上的球扁鋼距離艙段耐壓殼體2c1(D-d)=0.42，開孔圓心在球扁鋼與非耐壓殼體的中心處，開孔半徑為r，其圓心距離耐壓殼體2c2(D-d)=0.71，托板夾角為α=9o。

圖5 剛性阻振質量與高傳遞損失托板結構示意圖Fig.5 Scheme of the composite pedestal structure with rigid vibration isolation mass and high transmission loss

以非耐壓殼體的典型測點的平均振動加速度級作為高傳遞損失復合托板減振效果的衡量目標，通過動力學優(yōu)化分析來得到最佳的開孔半徑和托板夾角。由于在托板上開孔破壞了結構的連續(xù)性，使得結構強度有所減弱，因此，在優(yōu)化設計過程中，除了先前需要的艙段總重量限制外，還應考慮艙段危險點的結構強度要求。

設計變量：復合托板上的開孔半徑r=0.100～0.150 m，間隔0.001 m；復合托板夾角 α=8°～10°，間隔 0.1°。

狀態(tài)變量：潛艇艙段總重量；基座邊界處橫剖面上的內表面應力 F1≤1.15σs=901.6 MPa；跨度中點處縱剖面上的中面應力 F2≤0.85σs=666.4 MPa；復合托板上的危險點應力 F3≤0.8σs=627.2 MPa。

目標函數(shù)：全頻域內非耐壓殼體典型測點的平均振動加速度級。

由于優(yōu)化模型只有一個目標函數(shù)，如果只選取單個頻率下考核點的振動特性為優(yōu)化目標，則無法全面反映圓柱殼艙段的全頻域內特性是否達到了最優(yōu)。因此，本文選取典型測點各頻率范圍內的平均振動加速度級為目標函數(shù)。

結構測點布置如圖6所示。對于結構測點的加速度響應值，按下式取平均振動級為：

圖6 結構測點布置示意圖Fig.6 Distribution of measuring points

式中，ai為各頻段上各頻譜分量的加速度響應值；a0為振動加速度基準值，本文取a0=1×10-6m/s2。

其中，目標函數(shù)取為：uobj=uobja*uobjb*…*uobjc*uobjd*uobje*1e30，其中 uobja為a頻段下各考核點的平均加速度響應值。

優(yōu)化采用零階方法，設置最大迭代次數(shù)為50，連續(xù)15次不收斂即退出循環(huán)。設計變量、狀態(tài)變量和目標函數(shù)的優(yōu)化序列結果如表1所示。圖7、圖8所示分別為優(yōu)化計算中作為目標函數(shù)的全頻域內非耐壓殼體典型測點平均振動加速度級和作為狀態(tài)變量的圓柱殼艙段總重量的迭代收斂曲線。

表1 高傳遞損失復合托板結構形式的優(yōu)化結果Tab.1 Optimal results of structural styles of composite pedestal with high transmission loss

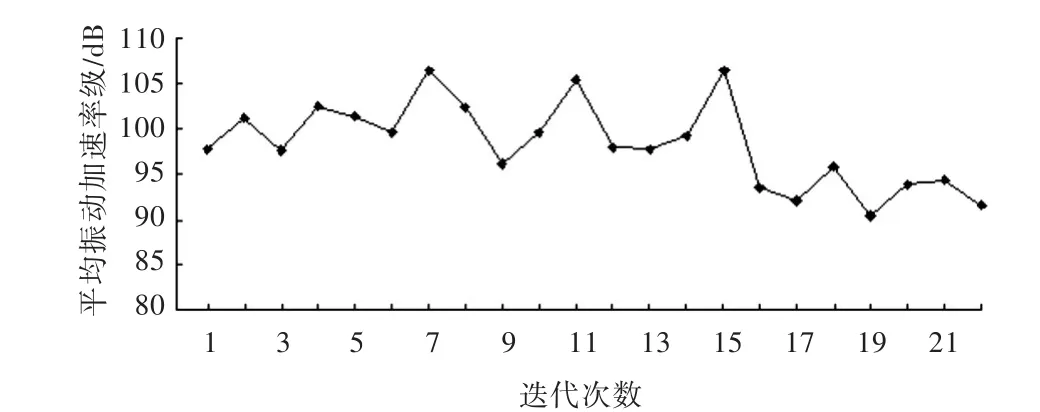
圖7 非耐壓殼體測點全頻域內平均振動加速度級—迭代次數(shù)曲線Fig.7 Iteration curve of the average vibration acceleration of the non-pressure hull for whole frequency

圖8 艙段總重量—迭代次數(shù)曲線Fig.8 Iteration curve of the cabin gross weight

由表1、表2中的數(shù)據(jù)及圖7、圖8中的迭代曲線可以看出，優(yōu)化循環(huán)迭代至第19次，目標函數(shù)結果便已收斂為最優(yōu)解，隔振效果最佳的高傳遞損失復合托板結構參數(shù)為：2c1(D-d)=0.42，2c2(D-d)=0.74，2r(D-d)=0.18，α=9.2°。通過將復合托板的剛性阻振質量塊等效為球扁鋼，同時優(yōu)化托板角度并在托板上開孔，艙段總重量便由184.14 t減少為167.63 t，減重10.08%。危險點的強度約束條件也均滿足。由于舷間結構的阻抗失配程度及不連續(xù)性得到了加強，優(yōu)化后，艙段非耐壓殼體全頻域內典型測點的平均振動加速度級由92.13 dB變?yōu)?0.47 dB，降低了1.66 dB，減低了振動波能量的傳遞，進而減少了輻射到流場中噪聲。

3 高傳遞損失復合托板結構隔振效果驗證

將舷間采用未優(yōu)化前的普通托板結構、剛性阻振質量托板結構和高傳遞損失符合托板結構的潛艇典型圓柱殼艙段結構模型分別導入軟件ABAQUS，并建立外流場以便考慮流固耦合作用的影響，同時，還可提取流場中的輻射聲壓。典型艙段圓柱殼結構流固耦合模型如圖9所示。參考文獻［9-10］，本文對比分析了優(yōu)化前、后不同托板結構對雙層圓柱殼振動聲輻射特性的影響。

圖9 艙段典型圓柱殼結構流固耦合模型Fig.9 Fluid-structure interaction model of submarine typical double cylinder shell

近場聲壓考核點的取法是在外流場中距離非耐壓殼1 m處，以正上方記為0°，每隔15°取一考核點，如圖10所示。

圖10 聲場考核點位置示意圖Fig.10 Scheme of the measuring points of the sound field

將各頻點下考核點的聲壓響應取平均，以衡量輻射聲場的強度。圖11給出了圓柱殼舷間結構分別采用普通托板、剛性阻振質量托板和高傳遞損失復合托板的潛艇典型艙段近場考核點平均輻射聲壓級隨頻率的對比曲線。

圖11 3種托板結構的平均輻射聲壓級對比曲線Fig.11 Comparison curves of average radiant sound pressure level of three kinds of pedestal structures

由圖可看出，低頻激勵時，3種托板結構的艙段近場考核點平均輻射聲壓級相差不大，復合托板的隔振效果不佳；在中、高頻激勵時，高傳遞損失復合托板和剛性阻振質量復合托板都有明顯的降噪作用，且后者略優(yōu)于前者。

4 結 語

本文將高傳遞損失復合托板的開孔半徑和托板角度作為設計變量，進行了在艙段總重量及強度要求約束下的全頻段的動力學優(yōu)化，得到了艙段非耐壓殼體平均振動加速度級隨迭代次數(shù)的變化曲線和優(yōu)化序列。通過優(yōu)化分析，得到了隔振效果最佳的高傳遞損失復合托板結構參數(shù)，艙段非耐壓殼體全頻域內典型測點平均振動加速度級降低了1.66 dB。

通過分析3種托板結構頻域內的近場輻射聲壓，驗證了高傳遞損失復合托板結構的隔振效果。在低頻激勵下，剛性阻振質量復合托板和高傳遞損失復合托板的隔振效果不佳，但對中、高頻結構噪聲有顯著的阻隔作用，且前者略優(yōu)于后者。

［1］劉見華.艦船結構聲傳遞的阻抑機理及應用研究［D］.上海：上海交通大學，2003.LIU J H.Study on the impending mechanism and application of the warship structure-borne sound propagation［D］.Shanghai：Shanghai Jiao Tong University，2003.

［2］胡忠平，冷駿.方鋼對艦船結構噪聲的傳播與阻隔機理分析［J］.機電設備，2008，25（4）：44-47.HU Z P，LENG J.Analysis of mechanism isolation vibration and transmitting of warships structure vibration wave by quadrate steel［J］.Mechanical and Electrical Equipment，2008，25（4）：44-47.

［3］石勇，朱錫，劉潤泉.方鋼隔振結構對結構噪聲隔離作用的理論分析與試驗［J］.中國造船，2004，45（2）：36-42.SHI Y，ZHU X，LIU R Q.Analysis and experimental research on the role of quadrate steel beam in isolating vibration wave［J］.Shipbuilding of China，2004，45（2）：36-42.

［4］姚熊亮，王強勇，孫明，等.剛性阻振質量在艦船基座設計中的應用研究［J］.中國艦船研究，2010，5（3）：8-12，21.YAO X L，WANG Q Y，SUN M，et al.Application research on rigid vibration isolation mass in ship pedestal design［J］.Chinese Journal of Ship Research，2010，5（3）：8-12，21.

［5］施引，朱石堅，何琳.船舶動力機械噪聲及其控制［M］.北京：國防工業(yè)出版社，1990.

［6］楊德慶，柳擁軍，金咸定.薄板減振降噪的拓撲優(yōu)化設計方法［J］.船舶力學，2003，7（5）：91-96.YANG D Q，LIU Y J，JIN X D.Structural topology optimal design to reduce vibration and noise of thin plate［J］.Journal of Ship Mechanics，2003，7（5）：91-96.

［7］KESSISSOGLOU N J.Active control of the plate energy transmission in a semi-infinite ribbed plate［J］.Journal of Acoustics Soc.Am，2000，107（1）：324-331.

［8］NJIFULOV A S.Ship structure acoustic design［M］.Beijing：National Defence Industry Press，1998.

［9］PANTELIDES C P，TZAN S R.Optimal design of dynamically constrained structures［J］.Computers and Structures，1997，62（1）：141-149.

［10］姚熊亮，劉慶杰，翁強，等.水下加筋圓柱殼體的振動與近場聲輻射研究［J］.中國艦船研究，2006，1（2）：13-19.YAO X L，LIU Q J，WENG Q，et al.Research on the vibration and near-field acoustic radiation of underwater ribbed cylindrical shell［J］.Chinese Journal of Ship Research，2006，1（2）：13-19.