最小二乘法在汽車銷售量預測中的應用

□文/陳秋玲 陳 忠

（武漢理工大學理學院 湖北·武漢）

對產品銷量進行預測是進行經濟決策活動的一個重要組成部分。運用定量預測模型對產品銷量進行預測方法有很多，本文運用的最小二乘法在產品銷售量預測過程中，使用的方法簡單明了，比較適合企業在進行預測產品產量時作為參考，從而能夠避免盲目的生產和經營，盡可能地為企業獲得最大利潤，以減少不必要的損失。

一、最小二乘法

在介紹最小二乘法之前，我們先來思考這個問題。如果變量y和x有精確的線性關系，這里可以假設y為因變量，x為自變量，有y=a1x+a0成立，我們得到，即觀測值等于回歸值。但是，在現實世界中，變量之間的關系未必都是線性的。受各種隨機因素的干擾，物與物之間沒有非常明確的對應關系。比如，產品的銷售量和供給量就是一種對應關系，而這種關系并非是y=a1x+a0所能確定的。那么，我們要得到銷售量和供給量之間的關系，就需要通過數學方法來建立銷售量和供給量之間的模型。而在處理類似的問題時，我們常常用到的是最小二乘法。

所謂最小二乘法，就是選擇合適的參數a0、a1，使得全部觀測的殘差平方和最小。用數學公式表示為:

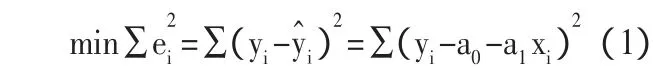
為了說明這個方法，先解釋一下最小二乘原理。因為不能利用總體回歸方程進行參數估計，所以我們選擇樣本回歸函數對總體進行估計，即:

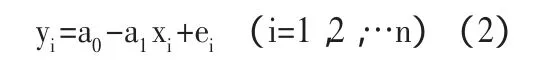
（2）式中:ei是殘差，等于真實值 yi減去估計值i。因此，為了使殘差ei盡可能的小，就需要選擇合適的估計量a0，a1，使總體回歸函數最優。

在經濟關系中，某一指標Y往往與多個因素X1，X2，…，Xm有關，如果這種關系具備一定的線性相關性，我們就可以利用多元回歸分析來處理這組數據。假設，我們令Y、X向量分別為:Y=（y1，y2，…，yn），X1=（x11，x21，…，xn1），X2=（x12，x22，…，xn2），Xm=（x1m，x2m，…，xnm），由X1，X2，…，Xm與Y之間存在的線性關系，得到n元線性預測公式:

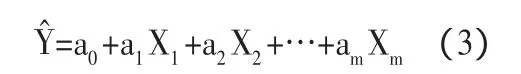
其矩陣形式為:

其中，我們稱待定常數 a0，a1，…，am為回歸系數。將每組觀測值代入（4）就得到:

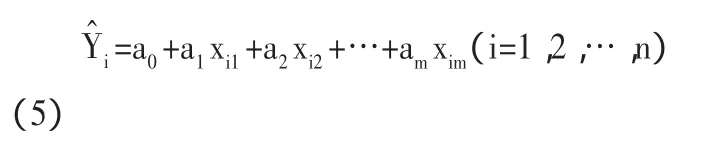
選擇的a0，a1，…，am，應使每個偏差e（ii=1，2，…n）都盡量小，因此，我們通常令偏差平方和為最小。這里，我們把S視為a0，a1，…，am多元函數，即:

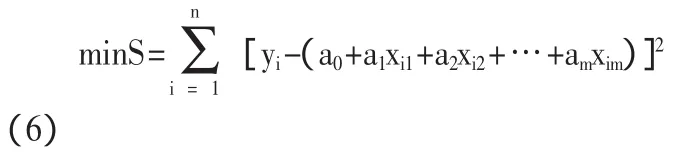
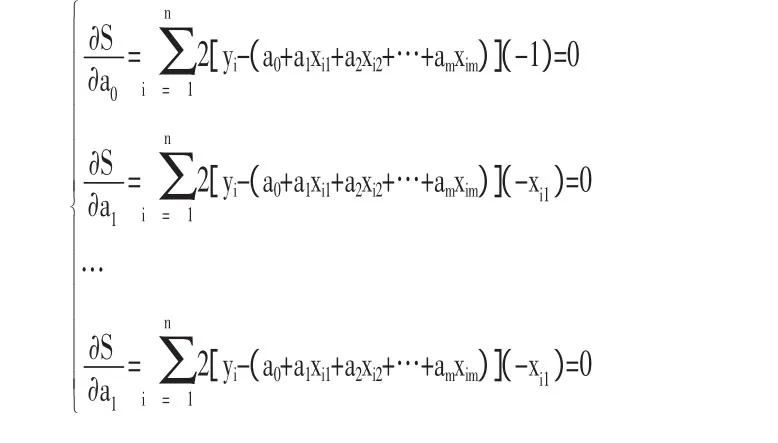
整理得:

將上述m+1個方程式聯立起來求a0，a1，…，am解，則得到公式（6）的待定系數值，從而確定了多元線性預測公式。

二、相關系數R

以兩個變量的情況為例，只要任意給定兩個變量x，y的一組數據，都可以經過計算給出一個經驗公式，但是這個公式在多大程度上反映了x，y的關系呢？因為只要通過最小二乘法采取強擬合我們同樣可以把一組毫無線性關系的數據表成線性關系，但這條直線并不能很好地反映了變量x和y的實際關系，缺乏應用價值。

為此，我們一方面要建立從經驗上認為有意義的方程，另一方面我們必須用數學方法對擬合效果和顯著性進行相關檢驗。相關系數是變量之間相關程度的指標，求相關系數的公式為:

表1 2001～2011年某紡織品銷售額數據表

由上面的式子可推算出:

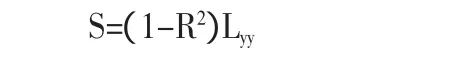
由于 S≥0，Lyy=≥0，我們可以得出 1－R2≥0，即 0≤≤1，所以越接近1，S的值就越接近0，x，y的線性關系就越好。

三、實例預測

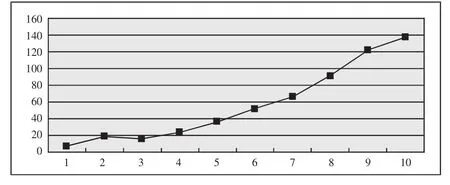
圖1 某品牌汽車2002～2011年總銷量曲線圖

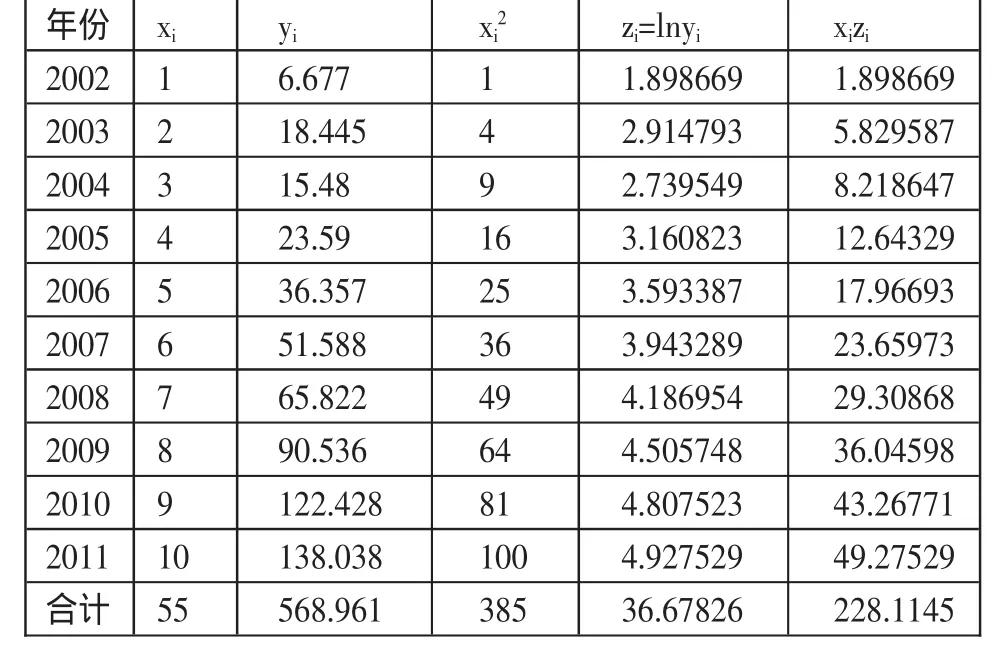
表2 經驗公式擬合處理后數據表

例:對某汽車品牌的汽車銷售量的擬合。我們選取汽車銷售量為因變量，單位為千輛，擬合銷售量關于時間x的趨勢曲線。以2002年為基準年，取值x=1；2011年x=10，2002～2011年的數據如表1。（表1）由散布圖1可以看出統計點是非線性的，它大致呈指數形分布。我們就取經驗公式y=αeβx來擬合這條曲線。（圖1）這個經驗公式所反映的點的排列是非線性的，我們可以通過取對數將其轉化為線性函數，從而運用最小二乘法確定這個線性函數。即:z=Ax+B，其中 z=lny，A=β，B=lnα，lny=lnα+βx，進而計算 α，β 的值。

取；xi=（1，2，…，11）；yi為各年銷售額；zi=lnyi，根據具體數據代入得到表格2。（表2）

查對數表得 α=6.746，將 β，α 代入（8）式中，因此得到了所求的經驗公式為:

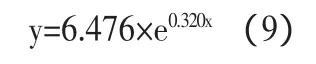
下面計算相應系數進行顯著性檢查:

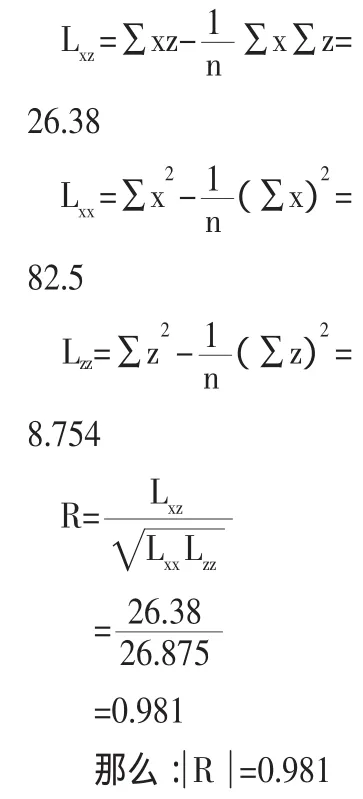
查看關系表（按α=0.01，n－2=11－2=9）得到回歸臨界值γα=0.735， 因 為=0.751＞γα=0.735，說明x，y間存在強相關關系，可以按公式:y=6.746×e0.320x進行外推預測，預測該企業2012年和2013年的銷售額為:

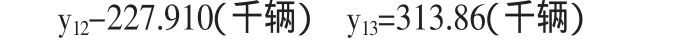
以上是根據散點分布趨勢選取曲線來擬合得出的結果，那么如果我們強行用線性關系即:=Ax+B來擬合曲線，會得出怎樣的結果呢？運用強行用線性關系，我們有:

四、小結

通過對具體實例的分析我們發現，如果某種產品在一個時期內銷量處于穩定增長的狀態，我們就可以對此種產品的未來銷量運用最小二乘法進行預測。但是，在選用曲線來擬合散點的過程中，我們必須依據散點的發展趨勢來正確的選擇曲線，否則有可能出現類似本文實例中出現的情況，即兩條曲線的顯著性系數都符合要求，都可以用來進行預測，但由于其中的一條擬合曲線沒有分析散點的發展趨勢，最后導致產生的誤差太大，因而不適宜運用在產品銷量的預測上。所以，企業在日常生產管理銷售過程中，科學有效的預測方法將在很大程度上決定企業的利潤，從而給經營者制定或者調整銷售計劃提供了可靠的理論依據。

[1]韓於羹.應用數理統計[M].北京:北京航空航天出版社，1989.

[2]徐天群，董亞娟.應用數理統計學習指導[M].武漢:武漢大學出版社，2002.

[3]方開泰，全輝等.實用回歸分析[M].北京:科學出版社，1988.

[4]岳苓水，趙寶貴.最小二乘法在商品銷售預測中的應用[J].石家莊:地質技術經濟管理，1997.1.

[5]杜國毅.最小二乘法在經濟預測中的應用[J].呼和浩特:內蒙古統計，2001.6.

[6]張金力，陳廣伏.最小二乘法在計量經濟模型中的應用[J].沈陽:沈陽航空工業學院學報，1999.4.