LCRⅡ型和Ⅰ型航空重力儀的同機飛行試驗*

孫中苗 翟振和 李迎春 肖 云

(西安測繪研究所，西安 710054)

LCRⅡ型和Ⅰ型航空重力儀的同機飛行試驗*

孫中苗 翟振和 李迎春 肖 云

(西安測繪研究所，西安 710054)

為檢驗和評價LCRⅡ型航空重力儀的精度和性能，與LCRⅠ型航空重力儀進行了同機飛行試驗。試驗結果表明，Ⅱ型與Ⅰ型航空重力儀相比，采樣點重力異常之差值的標準差為4.0×10-5ms-2，單套重力儀的測量精度約為2.8×10-5ms-2;5'×5'格網平均重力異常之差的標準差為4.9×10-5ms-2，每套系統獲得的5'×5'格網平均重力異常的精度為3.5×10-5ms-2，剔除兩個可疑值后，精度為2.9×10-5ms-2。總體上，LCRⅡ型航空重力儀與Ⅰ型精度相當，但具有更快的儀器穩定速度。

航空重力測量;航空重力儀;重力異常;低通濾波器;同機飛行

1 引言

顧名思義，航空重力測量是利用航空重力儀(或其他加速度計)在空中測量地球重力場信息的一種重力測量方法。2002年，我國首套航空重力測量系統(CHAGS)正式投入使用［1］，迄今已取得較為滿意的成果［2-4］。首套CHAGS的重力傳感器分系統采用美國LaCosteamp;Romberg公司的S/A型(Ⅰ型)海空重力儀。該公司在2002年對I型海空重力儀的控制系統部分進行了較大幅度的全數字化改進，主要包括:1)采用Microsoft Windows界面取代DOS界面;2)控制柜和傳感器一體化的緊湊設計; 3)可輸入GPS時間;4)采用內部高精度銣鐘進行時間同步;5)所有需用手工調整的程序簡化為通過軟件用戶界面進行調整;6)設備配置操作更加簡單; 7)采用用戶可調的FIR低通濾波器，代替原來的IIR低通濾波器;8)開機自動檢測、校準;9)自動記錄內外溫度、氣壓等環境參數。改進后的系統即“海空重力系統II”(LCRⅡ)具有界面友好、更緊湊、能自包含等優點，但其核心部件即重力傳感器和陀螺穩定平臺未加改進。

在第二套CHAGS中，我們采用了LCRⅡ型航空重力儀。為檢驗和評價該新型設備的精度和性能，2007年8月在某中等山區與LCRⅠ型航空重力儀(其精度和性能已經過多次試驗驗證)進行了同機飛行試驗。本文將介紹同機試驗的有關情況，并對兩套重力儀的精度進行詳細比較和分析。

2 數據處理方法概述

2.1 數據處理模型

航空重力測量采用相對重力測量原理，在飛機起飛前、降落后航空重力儀需作靜態觀測，以將重力觀測值與停機坪的重力基準值相聯系。航空重力標量測量的基本數學模型為［2，5］:

式中，Δg表示測線采樣點的重力異常;gb系停機坪處的重力基準值;fZ為比力及其初值;˙vU為飛機垂直加速度;δaE為厄特弗斯改正;δaH為水平加速度改正;δaF系空間改正;γ0系正常重力。

比力fZ的計算公式為:

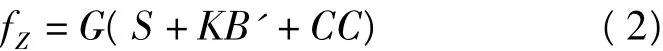
式中，G為格值，用于將重力計數單位轉換成毫伽單位;S為彈簧張力;K為擺桿尺度因子，即K因子;B'為擺桿速度，可由擺桿位置差分求得;CC為交叉耦合改正。

對于第一套系統，交叉耦合改正CC在重力儀中有直接輸出;而LCRⅡ型航空重力儀中沒有直接輸出，需要由交叉耦合的5個線性監視項按下式計算得到［6，7］。

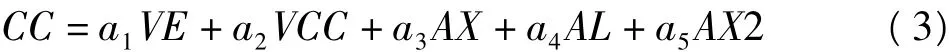
式中，VE、VCC、AX、AL、AX2分別是5個CC監視項的名稱，ai(i=1，…，5)為CC系數。

式(1)中除停機坪處的重力基準值gb外，(fZ-+δaH)需由重力儀觀測值計算得到，而其余各項均由GPS數據算得。顯然，若采用相同的GPS數據，(fZ-+δaH)實質上反映了重力儀的不同。此外，受大氣湍流和飛機長周期運動等因素影響，由式(1)直接求得的重力異常中含有大量高頻噪聲，因此，需進行低通濾波處理以將測量噪聲降低至可以接受的水平。

2.2 低通濾波器設計

低通濾波器的主要作用是減弱或消除航空重力測量觀測值中的高頻噪聲。飛機垂直加速度一般可以達到0.5 ms-2(RMS)，峰值有時高達幾ms-2。對低湍流情況，未濾波重力異常的RMS值為0.02～0.05 ms-2;對于高湍流RMS可達0.2 ms-2，故噪聲完全淹沒了實際的重力異常信號。但由于這些噪聲通常表現為高頻特性，故采用低通濾波器可以有效地消除或減弱其影響。

低通濾波器的設計與應用需兼顧待求重力異常的空間分辨率和精度。短周期的低通濾波器有利于提高空間分辨率，但難以保證精度，反之亦然。無限沖激響應濾波器(IIR濾波器，如RC濾波器、巴特沃思濾波器)和有限沖激響應(FIR)濾波器是航空重力測量中常用的兩類低通濾波器。按照空中原始重力異常的頻譜特性以及分辨率和精度要求，我們自行設計了級聯式巴特沃思濾波器［2］，其幅頻響應示于圖1。低通濾波器的截止頻率為0.003 3 Hz，相應的時域周期為300 s，當飛機飛行速度為250 km/h時，對應的半波長分辨率約為10 km。

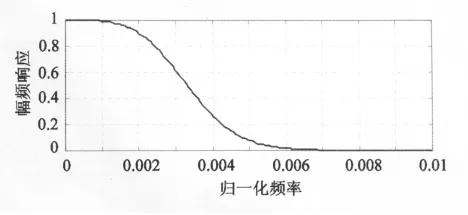
圖1 級聯式巴特沃思濾波器的幅頻響應Fig.1 Amplitude response of the cascade Butterworth filter

3 試驗結果與分析

3.1 試驗概況

試驗區域屬于中等山區，最高海拔2 100多米。試驗分為兩種情況，一是搭載試驗，在第一套航空重力測量系統作業時搭載LCR II型航空重力儀，即兩套重力儀同機試驗;二是第二套航空重力測量系統的單獨試驗。

試驗運載平臺為某型航測機，測量期間的平均飛行速度為250 km/h，飛行高度為2 800 m。在飛行區域內布設了3個GPS地面觀測站，飛機上安裝了2個GPS動態天線，實現飛機的動態差分定位。測量一般于每天的8:00～18:00進行，測量條件屬于中等湍流條件。

為便于比較，以下僅給出同機搭載試驗情況。搭載試驗測線數為18條，其中南北12條，東西6條。搭載試驗時GPS觀測數據完全相同，不同的是航空重力儀的觀測數據。LCRⅡ型航空重力儀的精度按如下三種方法進行分析和比較，一是以各采樣點的重力異常之差;二是以5'×5'格網平均重力異常之差;三是以各自交叉點不符值。

3.2 采樣點的重力異常之差

利用相同的GPS觀測數據和第一、第二套航空重力儀觀測數據，可以分別求得各條測線每個采樣點的重力異常。采樣點的重力異常之差反映了兩套航空重力儀的差異。不失一般性，我們選擇了飛行測量條件較好的10條測線進行了比較。10條測線的重力異常的互差統計于表1。

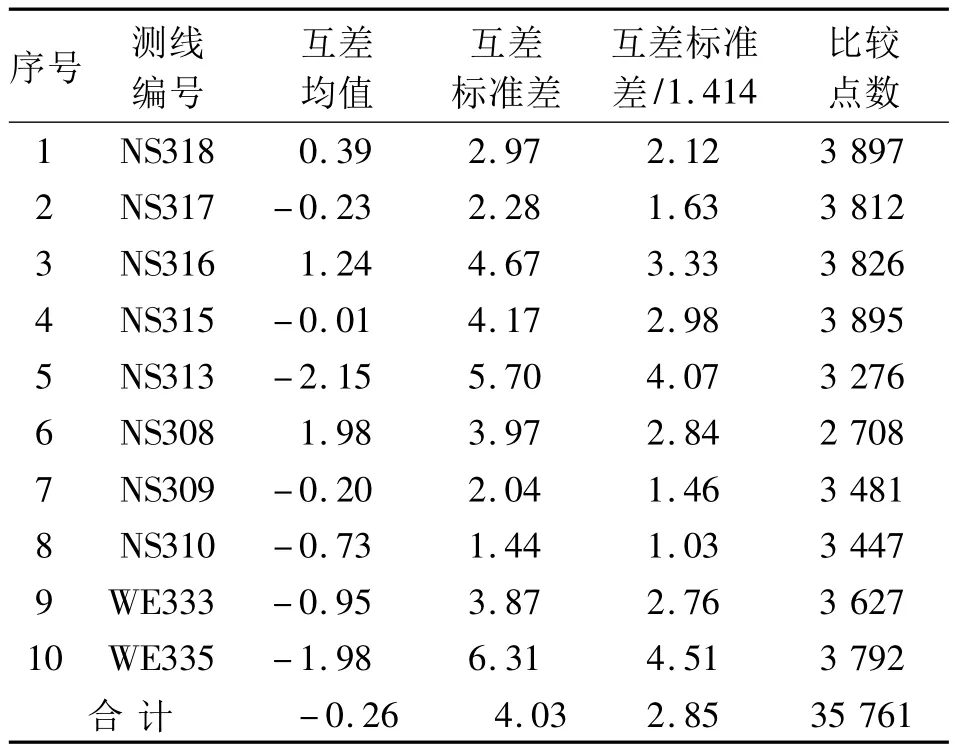
表1 采樣點的重力異常之差統計(單位：10-5ms-2)Tab.1 Differences of the gravity anomaly for the sample points(unit：10-5ms-2)

從表1可以看出，采用相同的GPS數據，由兩套航空重力儀觀測數據計算得到的采樣點的重力異常非常吻合，其差值的標準差為4.0×10-5ms-2。顧及兩套重力儀的觀測值互為獨立，并假設兩套航空重力儀的觀測精度相當，則每套重力儀的測量精度約為2.8×10-5ms-2。

應當指出的是，上述的航空重力儀觀測值尚包含了水平加速度改正的影響，因此與純粹的航空重力儀觀測值在概念上是有所區別的。也就是說，重力異常互差的標準差中還包括了水平加速度改正誤差的影響。

3.3 格網平均重力異常之差

航空重力測量的最終產品通常是格網平均重力異常，為此我們將測線重力異常構成空中5'×5'格網平均重力異常，以此比較兩套重力儀的精度。此處，我們構成了107個5'×5'格網平均重力異常。圖2示出了格網平均重力異常之差，圖2中符號‘×’表示差值為負值，符號‘×’表示差值為正值，各符號的大小反映了差值的大小，差值統計于表2。

由表2可見，107個5'×5'格網平均重力異常之差的標準差為4.9×10-5ms-2。現仍假設兩套航空重力儀的觀測精度相當，則由每套系統獲得的5'× 5'格網平均重力異常的精度為3.5×10-5ms-2。由圖2可見，差值中有兩個可疑值，將其剔除后，精度為2.9×10-5ms-2。

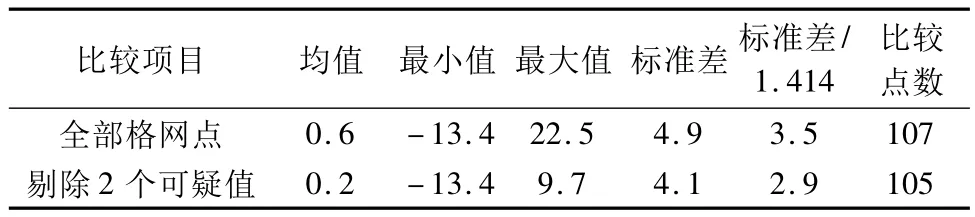
表2 5＇×5＇格網平均重力異常之差統計(單位：10-5ms-2) Tab.2 Differences of the mean gravity anomaly for 5＇×5＇grid(unit：10-5ms-2)

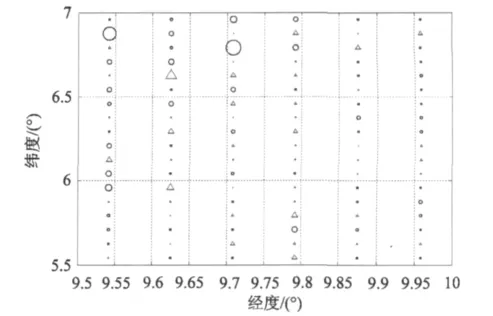
圖2 5'×5'格網平均重力異常之差Fig.2 Differences of the mean gravity anomaly for 5'×5' grid

3.4 交叉點不符值

利用兩套系統各自的交叉點不符值，能夠大致評價兩套系統的性能。對于搭載試驗的18條測線，可以構成58個交叉點。表3是交叉點不符值的統計結果。

表3 交叉點不符值統計(單位：10-5ms-2)Tab.3 Statistics of crossover errors(unit：10-5ms-2)

從表3可知，第一套系統的交叉點不符值要比第二套系統的大些，這具體反映在標準差上。但利用抗差估計［8］，即根據交叉點不符值的大小賦以不同權系數后，兩者的標準差趨于一致。交叉點平差后，精度有所提高。總體而言，第二套系統的精度略優于第一套系統。

此外，從作業過程以及數據處理過程中我們發現，第二套航空重力儀要比第一套穩定得快，即在相同的作業時間內，第二套系統的有效觀測數要多些。圖3示出了測線NS308的相關情況，顯然第一套系統的兩端數據難以接受。

圖3 兩套重力儀穩定速度的比較Fig.3 Comparison of the stable time for the LCR gravimeterⅡandⅠ

4 結論

1)基于相同的GPS數據，由兩套航空重力儀觀測數據計算得到的采樣點的重力異常非常吻合，其差值的標準差為4.0×10-5ms-2。顧及兩套重力儀的觀測值互為獨立，并假設兩套航空重力儀的觀測精度相當，則每套重力儀的測量精度約為2.8× 10-5ms-2。

2)采用同樣的GPS數據，107個5'×5'格網平均重力異常之差的標準差為4.9×10-5ms-2，每套系統獲得的5'×5'格網平均重力異常的精度為3.5 ×10-5ms-2，剔除兩個可疑值后，精度為2.9×10-5ms-2。

3)對于同樣的交叉測線，第一套系統的交叉點不符值的標準差要比第二套系統的相應值大些。抗差估計后，兩者趨于一致。第二套系統的總體精度略優于第一套系統，且第二套航空重力儀的穩定時間比第一套稍短，即在相同的作業時間內，第二套系統可獲得更多的有效觀測。

1 夏哲仁，等.航空重力測量系統(CHAGS)［J］.測繪學報，2004，33(3):216-220.(Xia Zheren，et al.Chinese Airborne Gravimetry System(CHAGS)［J］.Acta Geodaetica et Cartographica Sinica，2004，33(3):216-220)

2 孫中苗.航空重力測量理論、方法及應用研究［D］.鄭州:信息工程大學.2004.(Sun Zhongmiao.Theory，methods and applications of airborne gravimetry［D］.Zhengzhou:Information Engineering University.2004)

3 孫中苗，等.平原地區航空重力測量的精度分析［J］.測繪通報，2006，10:1-4.(Sun Zhongmiao，et al.Accuracy evaluation of airborne gravimetry over plain area［J］.Bulletin of Surveying and Mapping，2006，10:1-4)

4 夏哲仁，等.航空重力測量系統試驗報告［J］.測繪科學與工程，2005，25(1):6-10.(Xia Zheren，et al.Test report of the Chinese airborne gravimetry system［J］.Geomatic Science and Engineering，2005，25(1):6-10)

5 Schwarz K P and Li Y C.An introduction to airborne gravimetry and its boundary value problems［M］.Como Italy: Lecture Notes of IAG International Summer School，1996: 312-322.

6 Vallioant H D.The LaCoste and Romberg air/sea gravity meter:an overview［M］.CRC Handbook of Geophysical Exploration at Sea，2nd edition，1991:159-165.

7 孫中苗，夏哲仁，李迎春.LaCosteamp;Romberg航空重力儀的交叉耦合改正［J］.武漢大學學報(信息科學版)，2006，31(10):883-886.(Sun Zhongmiao，Xia Zheren and Li Yingchun. Cross-coupling correction for LaCosteamp;Romberg airborne gravimeter［J］.Geomatics and Information Science of Wuhan University，2006，31(10): 883-886)

8 Yang，Y.Robust estimation for dependent observations［J］.Manuscripta Geodaetica，1994，19:10-17.

CONCURRENT FLIGHT TEST OF LaCosteamp;Romberg(LCR) AIRBORNE GRAVIMETERⅡANDⅠSYSTEM

Sun Zhongmiao，Zhai Zhenhe，Li Yingchun and Xiao Yun
(Xi’an Research Institute of Surveying and Mapping，Xi’an 710054)

In order to validate the accuracy and the performance of the LaCosteamp;Romberg(LCRⅡ)，a concurrent flight test over a mountain area was undertaken.The LCR gravimeterⅡand an LCR gravimeterⅠsystem side by side.The results of the flight test show that the standard deviation of the gravity anomalies difference measured with the two systems is about 4.0×10-5ms-2namely the accuracy of the single system is about 2.8×10-5ms-2if we assumed the two systems have the same accuracy.They also indicate that the standard deviation of the 5' ×5'grid mean gravity anomalies difference from the two systems is about 4.9×10-5ms-2namely the related accuracy of the single system is about 3.5×10-5ms-2and 2.9×10-5ms-2after two outliers were eliminated.In general，LCR gravimeterⅡsystem has the identical accuracy as the LCR gravimeterⅠsystem，but it can be quickly leveling off.

airborne gravimetry;airborne gravimeter;gravity anomaly;lowpass filter;concurrent flight

1671-5942(2012)02-0024-04

2011-12-27

國家自然科學基金(41174017)

孫中苗，男，1968年生，研究員，博導，博士。現從事航空重力測量理論與方法研究.E-mail:sun_szm@sina.com

P223+.4

A