無線激光通信圖像去噪技術

翟蓓蓓，孫運強，姚愛琴，趙曉東

（中北大學，儀器科學與動態測試教育部重點實驗室， 山西太原 030051）

0 引言

人們利用光通信已經有幾千年的歷史了，從古代的烽火傳遞消息，到近代軍隊的“旗語”，都是光通信的樸素應用；而現代的光纖通信，更是將光通信推向新的高度。光纖通信以其極高的通信碼率得到了人們的廣泛應用，與微波通信相比，光通信及其靈活的通信方式在某些領域仍有不可替代的作用。而無線激光通信則結合了微波通信和光纖通信的優點。

無線激光通信是涵蓋多種領域的綜合性技術，其關鍵技術問題主要有兩個方面：一是遠距離激光信號的發射與接收技術，其發送和接收信號的距離從上千萬米的空間激光通信，到幾十千米的地面激光通信；二是激光信號的捕獲和自動跟瞄技術。其具體的技術表現在5個方面:(1)光源及

高碼率調制技術；(2)大氣信道的研究；(3)精密、可靠、高增益的收發天線；(4)高靈敏度抗干擾的光信號接收技術；(5)快速、精確的捕獲、跟蹤和瞄準技術。

1 圖像去噪方法研究

1.1 圖像去噪處理

圖像去噪聲處理從整個圖像分析的流程上來講屬于圖像的預處理階段，從數字圖像處理的技術角度來說屬于圖像恢復的技術范疇，它的存在有著非常重要的意義，主要表現在：

(a)由于不同的成像機理，得到的初始圖像中都含有大量不同性質的噪聲，這些噪聲的存在影響著人們對圖像的觀察，干擾人們對圖像信息的理解。噪聲嚴重時候，圖像幾乎產生變形，更使得圖像失去了存儲信息的本質意義。顯然，對圖像進行去噪處理是正確識別圖像信息的必要保證。

(b)除了能提高人視覺識別信息的準確性，對圖像進行去噪的意義還在于它是對圖像作進一步處理的可靠保證。如果對一幅含有噪聲的圖像進行特征提取、配準或者圖像融合等處理其結果肯定不能令人滿意，所以圖像去噪是必要的。

1.2 圖像空間域去噪

鄰域平均法是一種局部空間域處理的算法。設一幅圖像f(x,y)為對M×N的陣列，處理后的圖像為g(x,y)。它的每個像素的灰度值由包含(x,y)鄰域的幾個像素的灰度值的平均值決定。即用下式得到處理后的圖像：

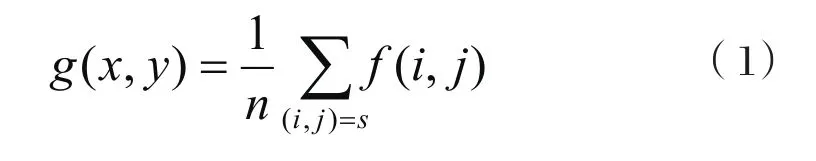
其中1≤x≤M, 1≤y≤N，S是以(x,y)點為中心的領域的集合，n是S內坐標點的參數。

圖1 4鄰域點(左)和8鄰域點(右)的集合

圖像鄰域平均法的處理效果與所用的鄰域半徑有關。半徑越大，則圖像的模糊程度也越大。另外圖像鄰域平均法算法簡單，計算速度快，但它的主要缺點是在降低噪聲的同時使圖像產生模糊，特別在邊緣和圖像細節處，鄰域越大，模糊越厲害為了減少這種效應，可以采取閾值法，也就是根據下列準則形成處理圖像。

其中T是一個規定的非負閾值，當一些點和它們鄰值的差值不超過規定的T閾值時，仍保留這些點的像素灰度值。這樣處理后的圖像比直接采用式（1）的模糊度要小。當某些點的灰度值與各鄰點灰度的均值差別較大時，它很可能是噪聲，則取其鄰域平均值作為該點的灰度值，它的處理效果仍然是很好的。為了克服簡單局部平均的弊病，目前已提出許多保留邊緣細節的局部平滑算法。它們討論的重點都在如何選擇鄰域的大小，形狀和方向，如何選擇參加平均的點數以及鄰域各點的權重系數等。如果將受噪聲干擾的圖像看成一個二維隨機場，則可以運用統計理論來分析受噪聲干擾的圖像平滑后的信噪比問題。在一般情況下，如果噪聲屬于加性噪聲，并且是獨立的高斯白噪聲（均值為零，方差為σ2），由信噪比定義為含噪圖像的均值與方差之比，則含噪圖像經鄰域平均法處理后，其信噪比將提高倍(n

為鄰域中包含的像素數目)可見鄰域取的越大，像素點越多，信噪比提高越多，平滑效果越好。

1.3 圖像變換域去噪方法

圖像變換域去噪方法是對圖像進行某種變換，將圖像從空間域轉換到變換域,再對變換域中的變換系數進行處理，再進行反變換將圖像從變換域轉換到空間域來達到去除圖像噪聲的目的。

頻率域低通濾波是基于傅里葉變換的去噪方法。而對于數字化的圖像，采用的是二維的離散傅里葉變換。以下是對二維離散傅里葉變換的介紹。

離散傅里葉變換在數字信號處理及數字圖像處理中應用十分廣泛。它建立了離散空間域和離散頻率域之間的聯系。

我國歷史上迄今保存最為完好的皇家藏書樓是皇史宬。嘉靖十三年（1534年）七月，明世宗效仿古代的“石室金匱”之制，開始在順天府（今北京）興建皇史宬。皇史宬用于專門收藏皇帝《寶訓》《實錄》《玉碟》等皇家典籍與貯存《永樂大典》副本，是我國迄今保存最為完好的皇家藏書樓。

(1) 二維離散傅里葉變換的定義

定義：二維離散信號{f(x,y)x=0,1,…,M-1;y=0,1,…,N-1}的離散傅里葉變換對為：

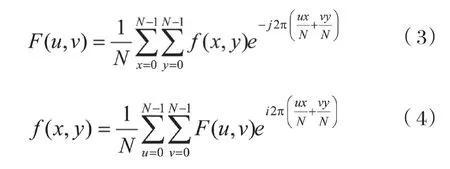
在大多數場合，假定圖像為方陣，即M=N，此時離散傅里葉變換的變換對可簡化為:

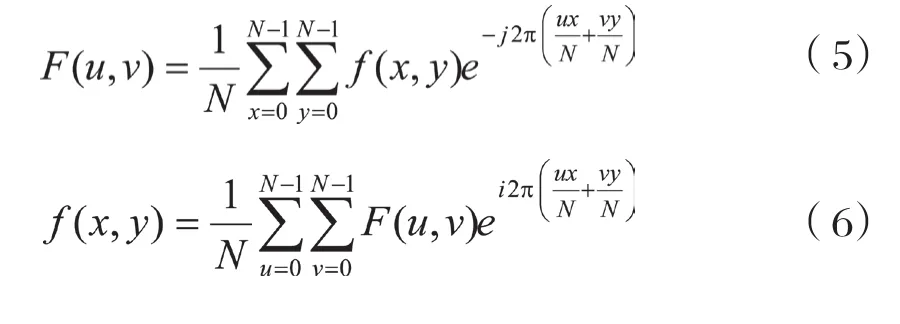
在離散傅里葉變換對中，F(u,v)稱為離散信號f(x,y)的頻譜，|F(u,v)|稱為幅度譜，φ(u,v)為相位譜，它們之間的關系為：

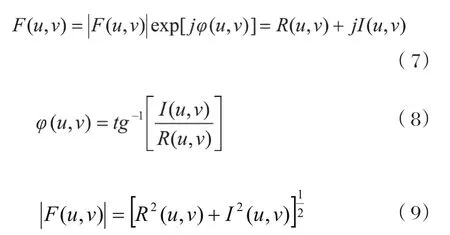
需要強調的是，離散變換一方面是連續變換的一種近似，而另一方面，其本身是嚴格的變換對。在以后進行的信號分析中，就可以簡單地直接把數字域上得到的結果作為對連續場合的解釋，兩者之間得到了統一。

(2) 二維離散傅里葉變換的性質

在二維情況下，存在和一維變換相同的性質，如線性、位移、尺度、卷積、相關等。下面介紹在二維情況下才有的兩條性質：

變換的可分離性由于離散傅里葉變換的指數項(變換核)可以分解為只含ux和vy的兩個指數項的積，因此，二維離散傅里葉正反變換運算可以分別分解為兩次一維離散傅里葉變換：

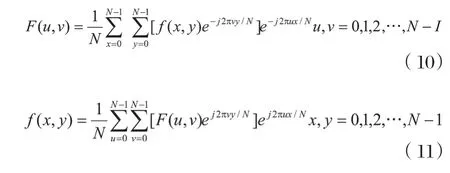
這一性質就是二維變換可分離性的含義。

若引入極坐標，使：

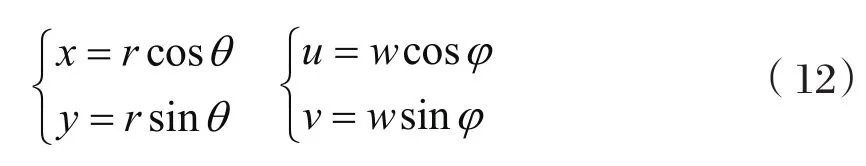
則f(x,y)和F(u,y)分別表示為f(r,θ)和F(w,?)，在極坐標中，存在以下變換對：

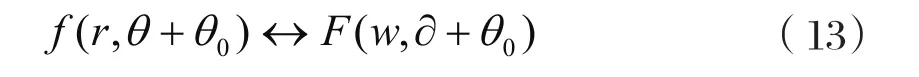
若將f(x,y)在空間域旋轉角度θ0，則相應地F(u,y)在頻域中也將旋轉同一角度θ0。

2 濾波結果分析

無線激光通信中，圖像噪聲有很多，如高斯噪聲、白噪聲和椒鹽噪聲等。本文主要針對高斯噪聲分析和比較了幾種典型的空域濾波法的特點，試圖通過在有噪聲的圖像上先進行低通濾波，然后高通濾波，找到一種恢復原始圖像輪廓的去噪聲方法。圖像的很多噪聲是高斯噪聲，本文就主要以它們為例，試圖在空域濾波法中，找到一種簡單、有效的去除噪聲方法。通過MATLAB實驗和分析幾種低通濾波和高通濾波的特點，得出了如下結論（結果見圖2～圖6）：相對于鄰域濾波法，對高斯噪聲的處理效果更好。濾波的效果都與采用的模板、模板的大小有很大的關系。不管是鄰域濾波法還是中值濾波法，由于都屬于低通濾波，會使圖像輪廓變得模糊，而高通濾波法中的基本高通濾波、高增益濾波、拉普拉斯算子濾波，以及拉普拉斯高斯算子，都可以使圖像銳化，輪廓變清晰。因此可以考慮采用兩者結合的方法對噪聲進行處理，經過反復實驗和分析，雖然沒有得到去除高斯噪聲的有效方法，但中值濾波結合拉普拉斯算子法或中值濾波結合拉普拉斯高斯算子法（需要作簡單的灰度變換），都可以有效地消除椒鹽噪聲，且使圖像輪廓基本上不變，其中中值濾波結合拉普拉斯算子法效果更好。

圖2 帶有高斯噪聲的rice圖像

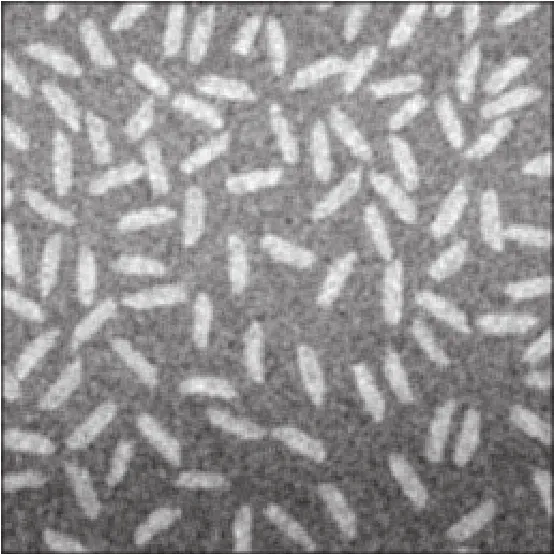
圖3 經領域平均法濾波后的帶有高斯噪聲的圖像

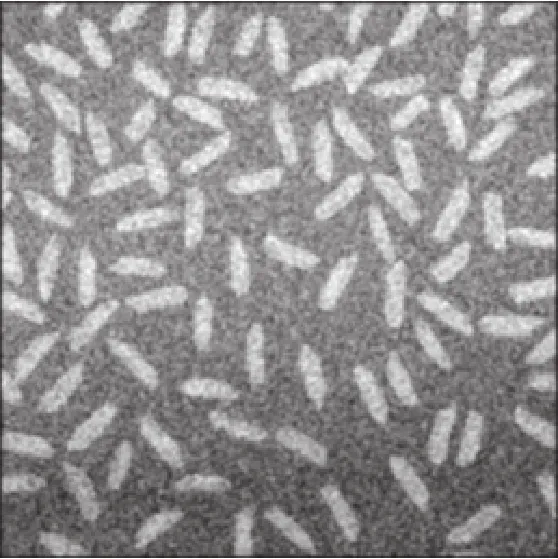
圖4 經高斯模板處理后的帶有高斯噪聲的圖像

圖5 模板處理后的帶有高斯噪聲的圖像

圖6 經中值濾波后的帶有高斯噪聲的圖像

3 結論

本文還對無線激光傳輸的圖像信號噪聲的處理進行了研究。在圖像信號傳輸過程中必然會因為噪聲的影響使得圖像失真甚至變形。為了使含噪圖像變得清晰，本文分析了幾種含噪圖像的去噪辦法。圖像去噪方法基本上可分為空間域法和變換域法兩大類，前者是在原圖像上直接進行數據運算，對像素的灰度值進行處理。它又分為兩類:一類是對圖像作逐點運算，稱為點運算：另一類是在與處理像素點鄰域有關的空間域上進行運算，稱為局部運算。變換域法是在圖像的變換域上進行處理，對變換后的系數進行相應的處理，然后進行反變換達到圖像去噪的目的。

[1]楊齊民,王崇真,鐘麗云,等.激光束與光纖耦合的研究[J].云南工業大學學報,1995,11(1):1-5.

[2]王俊峰,聶吉金.空間激光通信技術及發展[J].西安通信學院學報,2005(6):15-22.

[3]陳根祥,秦玉文,趙玉成,王勇譯.光通信技術與應用[M].北京:電子工業出版社,1998:38-45.

[4]王俊生,田波,崔一平.大氣激光通信技術[J].電子器件,2005:79-86.

[5]胡晟,艾勇.自由空間光通信中氣象因素影響分析[J].光學與光電技術,2005:23-32.

[6]趙春暉,王偉.全方位多結構元形態濾波器[J].中國圖像圖形學報,1997,18(6):210-226.

[7]Akopian D,Vainio,Agaian,Astola.Processors for generalized stack filters[J].IEEE Trans,1995,43:1541-1546.

[8]劉極峰，原紅玲.快速成型中激光燒結成型技術及應用[J].河南機電高等專科學校學報,2002,10(2):26-29.