基于滑模矢量控制的異步電機調速系統★

李 琳， 雷 蓓

（西安石油大學 陜西省鉆機控制技術重點實驗室， 陜西西安 710065）

0 引言

異步電動機具有結構簡單、牢固耐用、過流能力大、容易維護及價格低廉等優點，廣泛應用在現代交流傳動系統中。相對直流電機，它是一個高階、非線性、強耦合的多變量系統，很難實現高動態性能。由于電力電子技術和交流電機控制理論的發展，許多現代控制方法應用到異步電機調速系統，如矢量控制、直接轉矩控制、滑模

控制等，使異步電機調速系統性能越來越好[1-2]。

1 異步電機的矢量控制

矢量控制是通過坐標變換的方法，將異步電動機模型等效成直流電機模型，分解異步電機的定子電流，使能獨立控制轉矩和磁場有關的兩個分量，實現對交流電動機轉速和磁鏈控制的完全解耦。矢量控制系統框圖如圖1所示。

圖1 矢量控制系統框圖

1.1 矢量控制變頻調速原理

根據矢量控制理論，遵循在不同坐標系下所產生的磁動勢完全一致的原則，經過三相——兩相變換和旋轉變換，將異步電機定子電流空間矢量進行分解，在轉子磁場定向坐標系(M-T)中將異步電機模型轉換為直流電機模型來進行控制。在沿轉子磁場定向的M、T 同步旋轉坐標系中,對于籠型轉子電機,轉子短路,則um2=ut2=0，數學模型中的電壓方程可簡化成公式(1)所示。

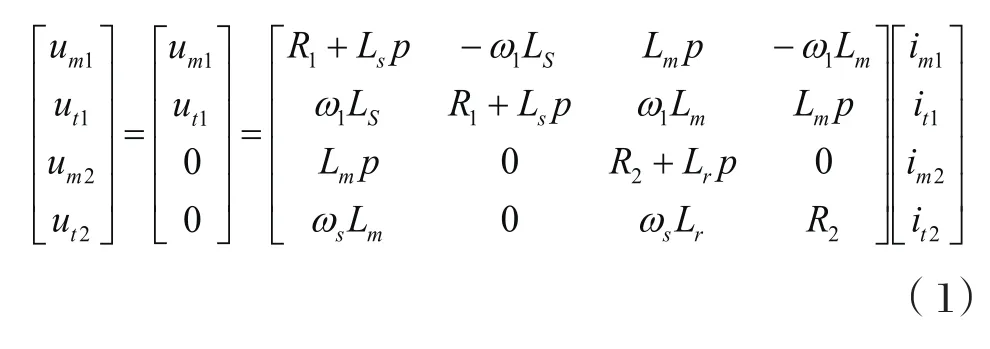
式中，um1,ut1為定子電壓矢量的M分量和T分量；R1，R2為定子和轉子電阻；Ls，Lr為定子和轉子繞組的自感；Lm為定轉子繞組間的互感；ω1為定子頻率的同步角速度；ωs為轉差角速度；p為極數。

在矢量控制系統中，被控制的是定子電流，因此必須從數學模型中找到定子電流的兩個分量和其他物理量的關系。

電流的勵磁分量為：

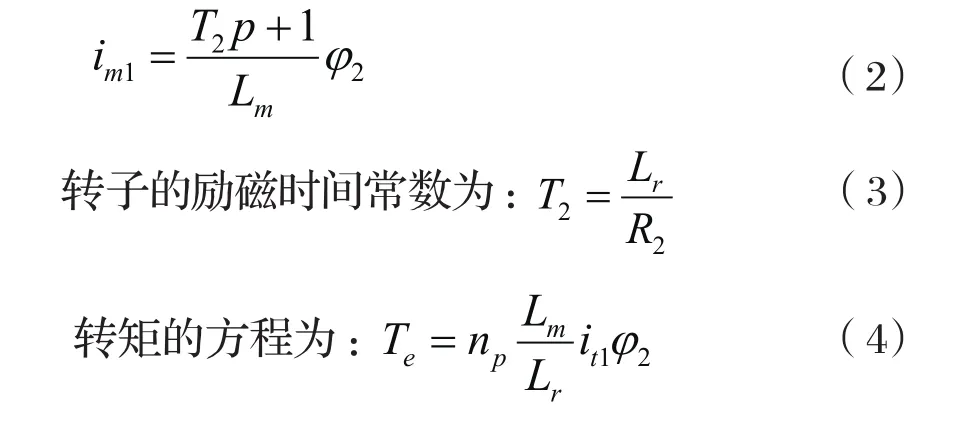
式中im1，it1為定子電流矢量的M分量和T分量；φ2為磁鏈；np為極對數。

總而言之，由于M、T坐標按轉子磁場定向，在定子電流的兩個分量之間實現了解耦（矩陣方程中出現零元素的效果），im1唯一決定磁鏈φ2，it1則只影響轉矩，與直流電機中的勵磁電流和電樞電流相對應，這樣簡化了多變量強耦合的交流變頻調速系統的控制問題[3]。

1.2 異步電機矢量控制系統的仿真模型

在MATLAB/Simulink建立異步電機矢量控制變頻調速系統的模型，它的仿真模型如圖2所示。

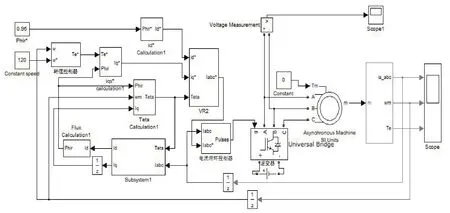
圖2 異步電機矢量控制變頻調速系統仿真模型

異步電機矢量控制變頻調速系統由轉速控制器、坐標變換、異步電機與逆變器、電流滯環控制器、、磁鏈觀測器和信號測量等子模塊組成。

為了使異步電機調速系統具有更好的穩定性，響應速度快，超調量小，將滑模控制加入系統。在異步電機調速系統中，轉速控制器采用的是PI控制，故針對它的轉速控制器進行分析。

1.3 轉速控制器模塊

轉速控制器的結構如圖3所示，其中積分器采用離散時間積分器Saturation元件用于對輸出轉矩限幅。

圖3 轉速控制器

PI控制器為：

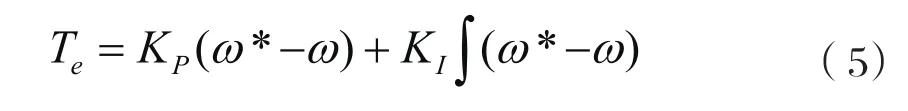
式中，KP為比例系數，KI為積分時間常數，ω*為給定的轉速，ω為電機的輸出轉速。

由圖2和圖3可以看出，異步電機矢量控制變頻調速系統中的轉速控制器采用的是PI控制，PI控制結構簡單，設計容易，但是隨著系統性能的要求不斷提高，傳統的PI控制已經不能滿足其要求。為了使異步電機矢量控制變頻系統更加穩定，提出將滑模控制運用到轉速控制器當中。

2 滑模控制器的設計

異步電機的參數(轉子電阻、定子電阻等)和負載參數(轉動慣量等)因地理環境變化而發生變化，異步電機的數學模型無法準確地反應調速系統的瞬態過程，使得一般的線性調節規律對交流調速系統有著一定的局限性[4]。滑模變結構控制是一種特殊的非線性控制，其非線性表現為控制的不連續性。它具有響應速度快，超調量小，控制精度高，較強的魯棒性與抗干擾等優點，并能適應有特殊控制要求的場合[5-6]。

滑模控制器結構如圖4所示，它的關鍵在于開關面函數的選取。

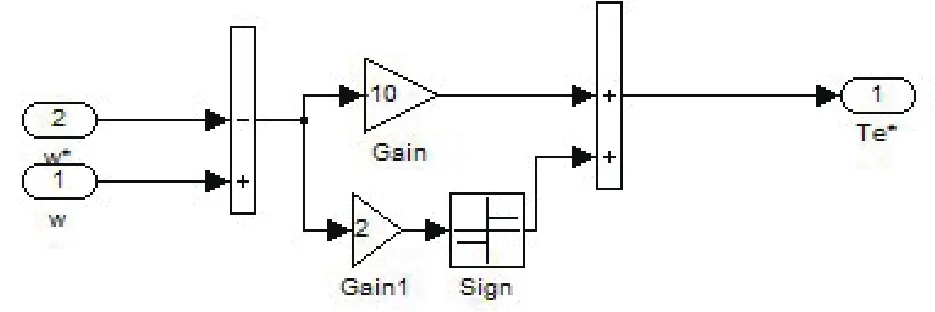
圖4 滑模控制其結構圖

定義開關面函數為：

速度環PI調節器采用滑模控制器，則滑模控制器設計為：

式中，Tes為轉矩的輸出，λ1、k為正常數。

3 仿真實驗

采用圖2 所示的仿真模型，對異步電動機矢量控制系統進行仿真。異步電動機的參數如下：額定功率3.7 kW；線電壓380 V；額定頻率60 Hz；定子內阻0.087 8 Ω；定子漏感0.8 mH；轉子內阻0.228 Ω ；轉子漏感0.8 mH；定轉子漏感34.7 mH；極對數為2；電流調節器采用滯環型的PWM 控制器，滯環寬度為20 A[7]。速度環PI控制下加負載的電機轉速圖形如圖6所示。轉速的給定值為120 r/s，PI控制器的參數KP=2，KI=20；滑模控制器的參數λ1=2，k=10。

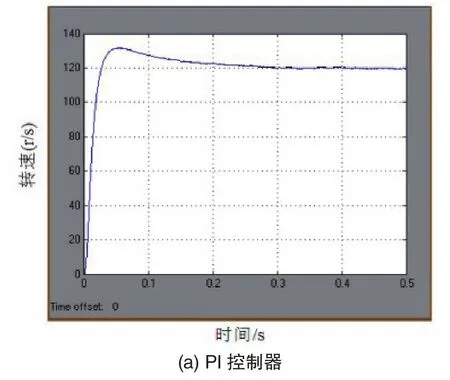
圖5 異步電機轉速的仿真圖形

由圖5可以看出，傳統的PI控制速度響應曲線超調較大，采用滑模控制速度響應曲線超調很小，響應速度很快，短時間內使系統達到穩定。

若在0.1 s的時候給電機突然加入負載，異步電動機的轉速負載如圖6所示。

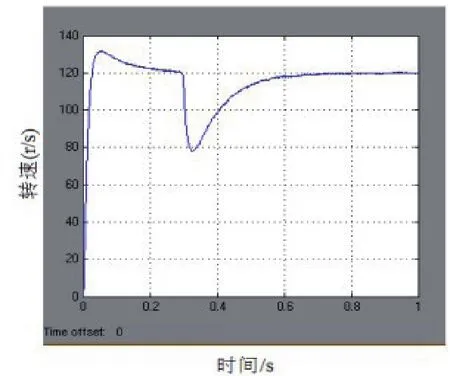
圖6 突加負載下異步電機的轉速

由圖6可以看出，給電機在0.3 s時突加負載，電機的輸出轉速突降到80 r/s，經過0.4 s之后，又恢復到120r/s,因而系統具有良好的抗負載擾動能力。

4 結論

針對異步電機運行過程中難以實現高動態性能的問題，建立了異步電機矢量控制變頻調速系統模型，運用了滑模矢量控制策略。該控制策略具有很好的控制特性，可以增強系統的抗干擾性，減少超調量，提高系統的響應速度。

[1]呂華林.異步電機矢量控制變頻調速系統的研究[D].武漢:武漢理工大學,2010.

[2]白晶晶.基于simulink的交流電機矢量控制調速系統的仿真[J].雞西大學學報,2008,8(3):86-89.

[3]陳伯時.電力拖動自動控制系統[M].北京:機械工業出版社,2000.

[4]胡俊達.基于遺傳算法的模糊自適應控制在DTC的應用[J].電工技術學報,2004,19(6):78-84.

[5]劉金琨.滑模變結構控制MATLAB仿真[M].北京:清華大學出版社,2005.

[6]胡俊,達胡慧.基于滑模變結構控制的異步電機速度控制的應用研究[J].大電機技術,2006(5):32-35.

[7]邵杰.基于Matlab/Simulink 異步電機矢量控制系統仿真[J].電氣傳動,2009,28(3):73-76.