飛蟲粘附翼型對翼型氣動特性影響的實驗研究

肖春生，焦予秦，高永衛

（西北工業大學 翼型葉柵空氣動力學國家重點實驗室，西安 710072）

0 引 言

由于NF－3風洞為直流風洞，風洞入口直接通外界環境，在夏天實驗時風洞內會吸入飛蟲，實驗時飛蟲會粘著在翼型模型表面，此種現象也正好與風力發電機葉片在戶外工作條件下情況相似。另外在復雜惡劣壞境中長期工作時風力機葉片發生腐蝕、覆蓋灰塵或者冰雪等，所有這些等于改變了翼型表面的粗糙度。由于粗糙度的大小和位置將影響到翼型的升力系數和阻力系數以及升力效率，同時也會影響到翼型的失速迎角［1］，因此國內外都開展了表面粗糙度對翼型氣動性能影響的實驗研究。東北農業大學開展了“附著物對直線翼垂直軸風機性能的影響”［2］的研究；汕頭大學對風力機翼型前緣表面粗糙度對氣動性能的影響也進行了實驗研究［3］，并得到了相關的試驗結果。但是目前所研究的引起粗糙度的元素主要是冰或者固體顆粒，未將自然界中的飛蟲作為元素來研究。

針對實際大氣情況下翼型表面會被飛蟲粘著的問題，進行了實驗探索，選用專門的風力機翼型研究表面粘著飛蟲后的氣動特性。

1 模型及實驗設備

1.1 實驗設備

實驗在西北工業大學NF－3風洞二元實驗段中進行。NF－3風洞為直流閉口試驗段風洞，二元試驗段寬3m，高1.6m，長8m，風速范圍20～130m／s，紊流度為0.045%。實驗模型（圖1）展長為1.6m，弦長為0.8m，剖面為相對厚度35%的翼型。

為了研究模型表面飛蟲的分布，將翼型表面共分為3個區（如圖1），第二區的上下邊界距模型展向中心線為200mm，總高400mm。第一區在第二區上方，高度400mm，第三區在第二區下方，高度為400mm。3個區域的寬度都為400mm，并以翼型前緣為對稱上下翼面各有200mm的寬度。每個區域的面積相等且為S＝0.4m×0.4m＝0.16m2，3個區域的總面積為0.48m2。

圖1 實驗模型Fig.1 Testing model

1.2 數據采集系統

數據采集系統采用美國PSI公司的9816電子掃描閥，共有683個壓力測量通道，采集速度為100Hz／ch，采集精度為±0.05%FS。該系統用來采集翼型的表面壓力和尾耙的壓力。

1.3 實驗方法

采用實驗模型豎跨試驗段上下壁的方法進行，在模型翼展中心處沿翼型上下表面開靜壓孔，測量翼型表面的壓力，用以計算翼型的升力和俯仰力矩；在模型后緣1.3倍弦長處安裝總壓排管，測量模型尾跡區的總壓分布和靜壓，用以計算翼型的阻力。

實驗內容如下：

（1）Re＝1.0×106時，實驗前擦拭模型和不擦拭模型（在進行一次Re＝4.0×106狀態實驗后）的對比實驗研究；

（2）實驗前擦模型，實驗起始迎角分別為α＝－10°、7°、9°和11°時4個變化過程時的對比實驗（Re＝4.0×106）研究；

（3）實驗前擦模型，α＝8°和α＝9°時連續實驗（Re＝4.0×106），每隔1s、30s和5min分別采集一次表面壓力分布，研究翼型表面大面積分離的時間和此時翼型表面的飛蟲數量。

實驗中的飛蟲為自然界的普通飛蟲，大小約為1.5mm，與翼型模型弦長的比值為0.001875。

2 實驗結果與分析

2.1 實驗前擦拭模型和不擦拭模型的對比研究

由圖2可以看出：Re＝1.0×106時，當實驗前未擦模型（此時模型上已經粘著有部分飛蟲），α＜－5°和α＞＋5°時翼型的升力線斜率明顯與實驗前擦模型的狀態不同，由0.0646變成0.1253，線性度不好；更為明顯的是其失速迎角降低了很多，由18°減小到了12°。圖3給出了對應的阻力特性對比，實驗前未擦拭模型狀態在迎角為9°時開始迅速增加，而實驗前擦拭模型狀態的阻力則是在迎角18°開始快速增加。說明當實驗前不擦拭模型時，隨著實驗的進行模型表面上的飛蟲數量持續增加，達到一定程度時引起了翼型上表面大面積的氣流分離，從而引起翼型提前失速，并引起阻力相應的快速增加。

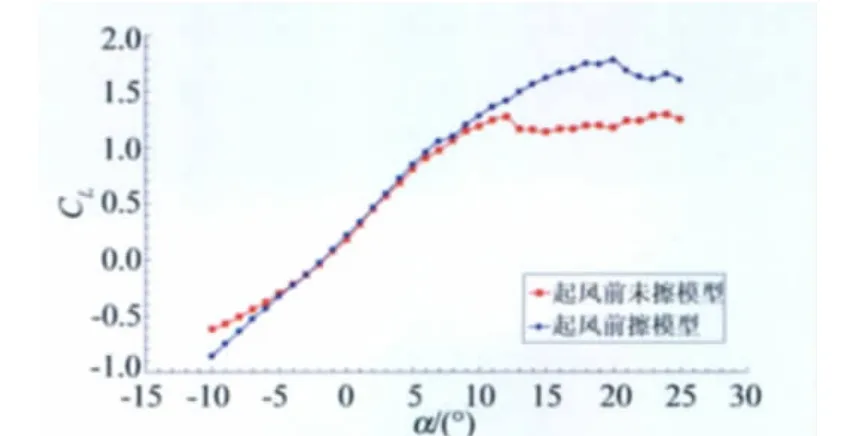
圖2 實驗前是否擦翼型的升力特性對比，Re＝1.0×106Fig.2 Lift characteristics contrast whether the airfoil model wiped or not before testing，Re＝1.0×106

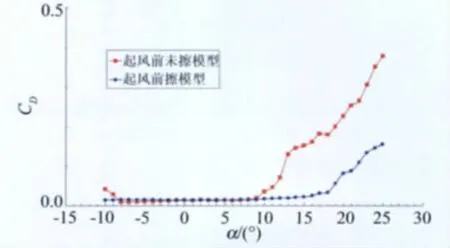
圖3 實驗前是否擦翼型的阻力特性對比，Re＝1.0×106Fig.3 Drag characteristics contrast whether the airfoil model wiped or not before testing，Re＝1.0×106

2.2 實驗開始迎角分別為－10°、7°、9°、和11°的對比研究

考慮到實驗過程中，模型表面粘著的飛蟲是隨時間逐漸增加的，因此專門研究了雷諾數為4.0×106時，實驗前將模型擦干凈，選擇不同迎角序列的對比試驗（起始迎角分別為：－10°、7°、9°和11°），圖4和5中給出相應的對比結果。

由圖看出迎角從－10°開始實驗時，翼型在迎角8°時失速；迎角從7°開始實驗時，翼型在迎角9°時失速；迎角從9°開始實驗時，翼型在迎角11°時失速；迎角從11°開始實驗時，翼型已處于失速狀態。對應的阻力特性曲線也呈現類似的規律。通過以上現象來分析，翼型的真實失速迎角是11°，但是在實際實驗時隨著時間的增加，模型表面粘著的飛蟲會大量增加，當達到某個臨界狀態時將會引起翼型失速，但是這個失速迎角（以下稱為表象失速迎角）并不是真實的失速迎角，從本次實驗結果來看，真實失速迎角與表象失速迎角之間有著非常大的差別（本研究有3°的差別）。針對風力機翼型而言，由于翼型要在復雜且惡劣的環境下工作，若翼型表面粘著了雜質、飛蟲等，將大大降低翼型的氣動性能。

圖4 不同迎角序列狀態下的升力特性對比，Re＝1.0×106Fig.4 Lift characteristics contrast with different beginning angle，Re＝1.0×106

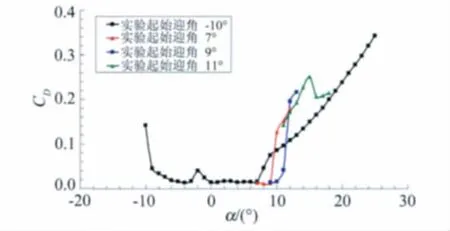
圖5 不同迎角序列狀態下的阻力特性對比，Re＝1.0×106Fig.5 Drag characteristics contrast with different beginning angle，Re＝1.0×106

2.3 表面飛蟲數量的實驗研究

首先在雷諾數為4.0×106，迎角為8°時，進行不同時間間隔周期采集壓力分布的對比實驗，時間間隔周期為1s、30s和5min。圖6為1s間隔周期采集的模型表面壓力分布曲線，可見當風速穩定后，83s之前壓力分布沒有發生變化并且沒有明顯分離區域，84s時翼型上表面距前緣60%弦長的位置發生了分離，1s后也就是85s時分離位置前移到50%弦長左右的位置，表明在從83～85s的2s內，模型表面粘著的飛蟲已經徹底改變了模型表面的流動狀態，而此后壓力分布則保持不變。分析認為可能由于飛蟲在翼型表面的粘著，改變了翼型前緣的流動狀態或者是相當于改變了翼型前緣的形狀引起了以上的突然變化。從停風后觀察，此時1區大致有15只飛蟲，2區有59只左右，3區有114只左右；按單位面積算，1區為375只／m2、2區為1475只／m2、3區為2850只／m2，對于整個觀察范圍平均為1567只／m2。一只飛蟲在模型表面的面積大約為1mm2，1567只飛蟲所占據的面積大約為1m2的0.16%。

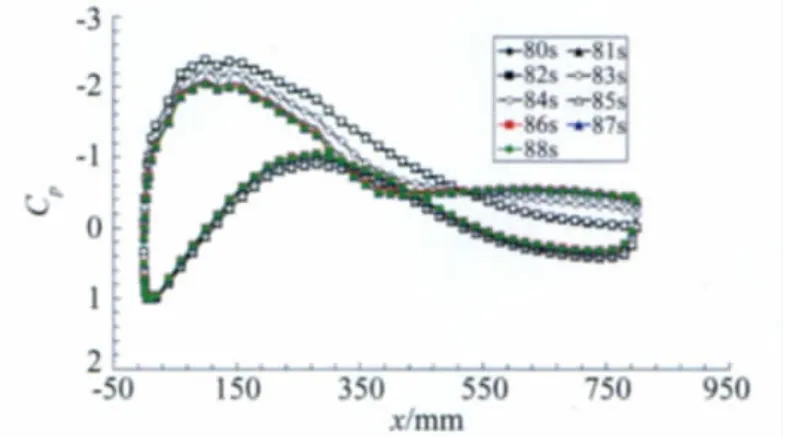
圖6 1s周期間隔采集的壓力分布曲線，α＝8°，Re＝4.0×106Fig.6 The pressure distribution curves of 1second periodic intervals acquisition，α＝8°，Re＝4.0×106

圖7為30s周期間隔采集的壓力分布曲線，翼型上表面的分離發生在90s的時候，忽略飛蟲粘著的不可確定因素以及時間間隔較長的原因，基本可以認為失速發生的時間與間隔1s所得到的失速發生時間相吻合。圖8也驗證了這個結論，分離是發生在前5min內。由此可以分析認為，當模型從負迎角開始實驗時，表面粘著的飛蟲逐漸增加，當累積到一定時間和數量時則會引起模型表面大面積的分離。

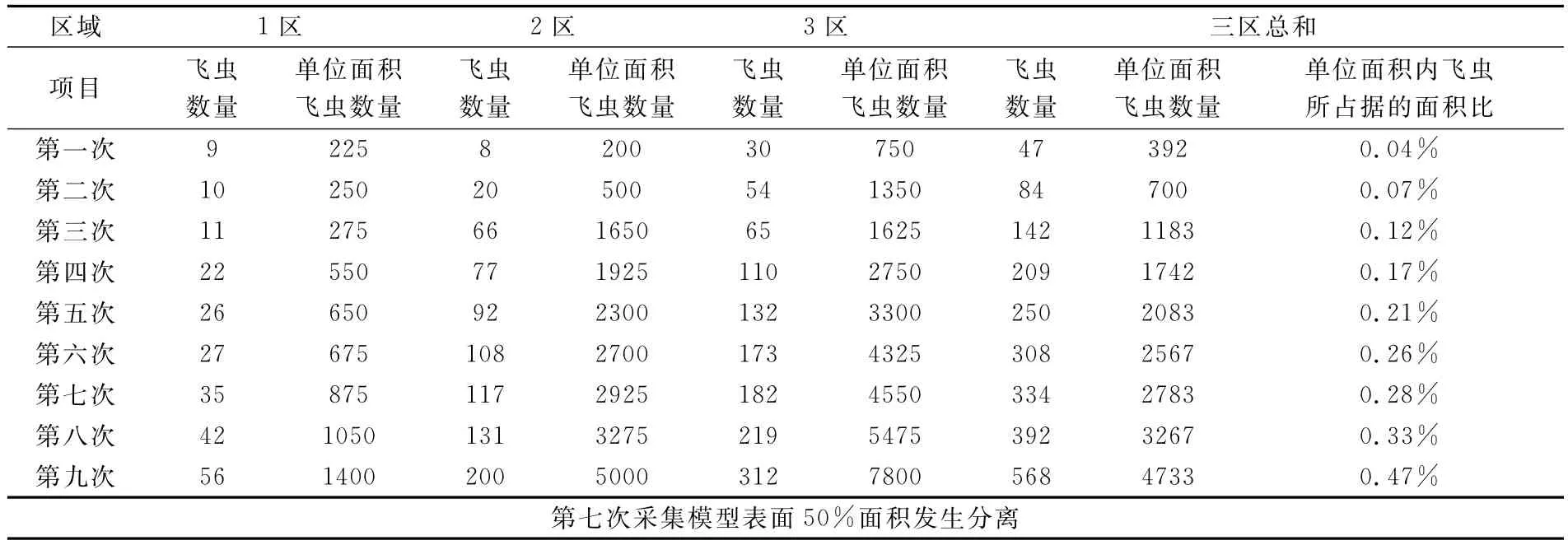
表1 Re＝4.0×106、α＝8°時翼型表面飛蟲數量表 單位：只、只／m2Table1 Winged insect quantity on airfoil surface，Re＝4.0×106、α＝8°

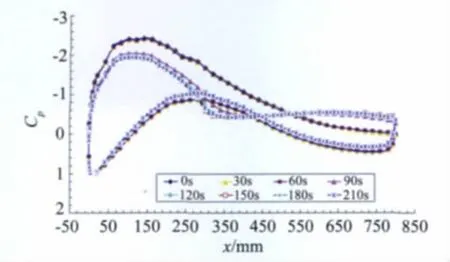
圖7 30s周期間隔采集的壓力分布曲線，α＝8°，Re＝4.0×106Fig.7 The pressure distribution curves of 30seconds periodic intervals acquisition，α＝8°，Re＝4.0×106

圖8 5min周期間隔采集的壓力分布曲線，α＝8°，Re＝4.0×106Fig.8 The pressure distribution curves of 5minutes periodic intervals acquisition，α＝8°，Re＝4.0×106

圖9為雷諾數4.0×106，迎角9°時時間間隔為1s采集的表面壓力分布。至于迎角9°的失速時間（139s）比迎角8°的失速時間（83s）晚的原因可能與表面飛蟲的數量和分布有關，但由于該實驗狀態下為連續測量，并沒有進行翼型表面飛蟲數量及分布的檢測。

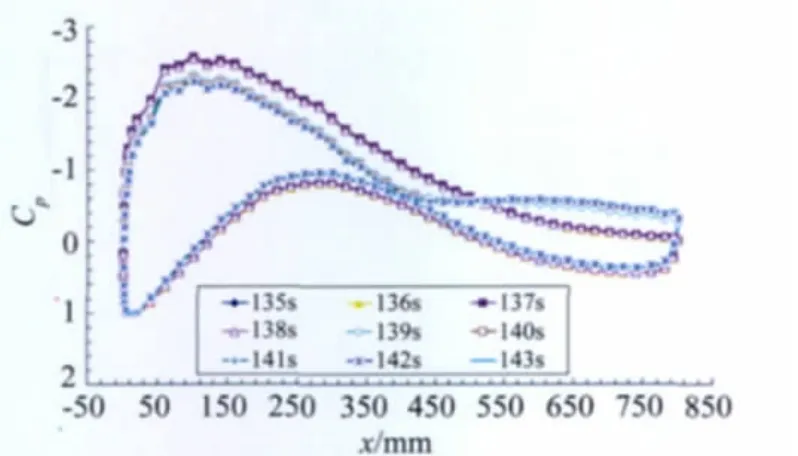
圖9 1s周期間隔采集的壓力分布曲線，α＝9°，Re＝4.0×106Fig.9 The pressure distribution curves of 1second periodic intervals acquisition，α＝9°，Re＝4.0×106

另外在雷諾數為4.0×106，迎角為8°時，實驗前擦凈模型，當風速穩定后立即采集表面壓力分布數據，隨即停風，并記錄模型表面飛蟲數量的實驗。曲線見圖10。圖中可見第七次采集時翼型模型表面有50%面積的分離區域。停風后模型表面3個區的飛蟲數量如表1，翼型表面的飛蟲圖像示意照片見圖11。

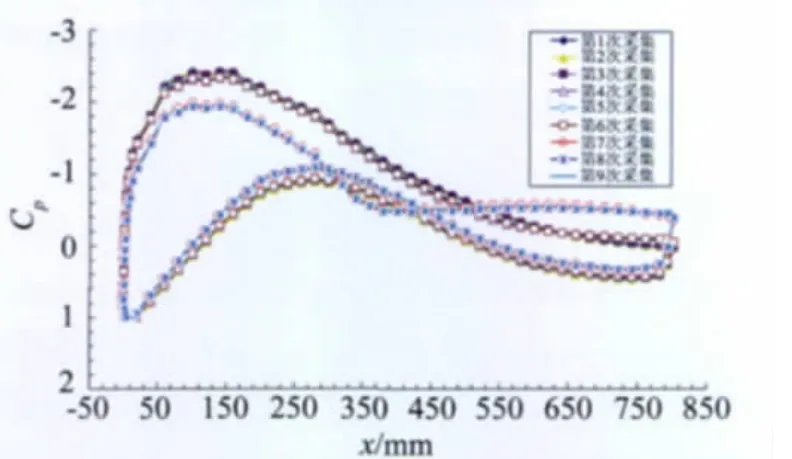
圖10 表面飛蟲數量研究的壓力分布曲線，α＝8°，Re＝4.0×106Fig.10 The pressure distribution curves of winged insect quantity on the surface，α＝8°，Re＝4.0×106

圖11 翼型表面飛蟲Fig.11 Winged insects on airfoil surface

由于飛蟲數量是在停風后測量出來的，那么前一次測量的飛蟲數量實際上為后一次測量開始前模型上已存在的飛蟲數量。表中顯示第七次采集后的飛蟲數量為334只，而第六次采集結束時為308只，兩者的飛蟲數量差距不是非常大，但是比雷諾數1.0×106時的188只多出很多，單位面積內飛蟲所占據的面積也由0.16%增加到0.28%。說明隨著雷諾數的增加模型表面粘著的飛蟲數量大量增加。

本次實驗只研究了模型表面飛蟲數量對翼型失速的影響，沒有對表面飛蟲的厚度影響進行研究。筆者認為當翼型表面的飛蟲數量達到一定量時，由于飛蟲厚度的增加，原始的翼型已經發展成了一個新的翼型，從而產生了不同的氣動特性，但由于無法測量飛蟲的厚度，所以還不能從實驗上進行驗證，但可以考慮通過數值計算模擬的辦法進行初步的計算分析。

3 結 論

通過風洞實驗研究，可得出以下結論：

（1）模型表面的飛蟲數量會改變翼型的失速迎角即表象失速迎角，該迎角與真實失速迎角有較大差別；

（2）模型表面粘著的飛蟲數量累計到一定程度時（蚊蟲的大小、數量、覆蓋的面積以及翼型本身特性的綜合因素），將會導致翼型表面50%區域以上的面積發生分離，引起翼型失速。

［1］ WALID Chakriun，ISSA AI－Mesri，SAMI AI－Fahad.Effect of surface roughness on the aerodynamic characteristics of a symmetrical airfoil［J］.Wind Engineering，2004，28（5）：547－564.

［2］ 李巖，田川公太郎.葉片附著物對直線翼垂直軸風力機性能的影響［J］.動力工程，2009，29（3）：292－296.

［3］ 包能勝，倪維斗.風力機翼型前緣表面粗糙度對氣動性能影響［J］.太陽能學報，2008，29（12）：1465－1470.

［4］ 王鐵城.空氣動力學實驗技術［M］.北京：國防工業出版社，1986.4