基于分形理論的自動舵液壓閥故障診斷方法研究
李天偉 , 樊明波 , 黃 謙 ,3, 李正友 ,4
(1.海軍大連艦艇學院航海系,遼寧 大連 116018;2.鎮江船艇學院,江蘇 鎮江 230013;3.海軍91257部隊,浙江 舟山 316001;4.解放軍69029部隊,新疆 烏魯木齊 830011)
0 引 言
自動舵液壓閥在其運行過程中必然產生振動,液壓閥狀態的改變將影響測得的振動信號,振動信號里包含了豐富的液壓閥狀態信號。當液壓閥出現油液污染、彈簧失效或閥芯磨損等問題時,將影響其正常換向,導致自動舵出現故障。液壓閥發生故障時,其振動信號突出表現為振動的非平穩和非線性。傳統的液壓設備診斷技術是針對振動信號的時域或頻域特征來提取特征量進行故障識別。實際上在不同的故障狀態下,其非線性因素的影響是不同的;因此,如何準確地刻畫液壓閥故障狀態對液壓閥的故障診斷是很有幫助的。
分形與混沌理論是當今非線性科學研究的一個重要且非常活躍的方面,它特別適合于各種“復雜現象”。分形理論中分形維數是定量刻畫混沌吸引子的一個重要參數,廣泛應用于非線性行為的定量描述中[1]。在設備故障診斷領域中,研究人員開始用分形維數對所測取的信號進行分析,并取得了一定的成果[2-4]。利用分形理論,不僅可以定性地分析系統的運動狀態,還可以通過計算與其唯一對應的分形維數對其運動狀態進行量化,從而實現對液壓設備的故障診斷。關聯維數作為分形維數的一種,對吸引子的均勻性反應敏感,更能反映吸引子的動態結構,只要捕捉到分形維數的變化情況,便可以對液壓設備故障作出診斷。
1 分形特征量計算
分形維數有很多種,本文選取了關聯維數作為分形維數實現對液壓閥的故障診斷,同時,依據液壓閥閥芯位移信號的特點,選取從時間序列計算關聯維數的G-P算法進行分形維數計算。
1.1 G-P算法
為了能夠從一維時間序列中得到動力系統相空間的幾何結構,Packard等人采用時間延遲技術重構相空間。1983年,Grassberger和Procaccia根據嵌入理論和重構相空間思想,提出了從時間序列直接計算關聯維數D2的算法,即G-P算法[1]。
長度為N的序列用時延法可以構成長度為Nm、維數為m的相空間。重構相空間的維數m稱為嵌入維數。設原始信號時間序列為{x1,x2,…,xN},重構的偽相空間軌道為

式中:τ——時間延遲;
i=1,2,…,Nm,Nm=N-(m-1)τ是重構相空間中向量的個數。
吸引子關聯維數由式(2)相關積分導出
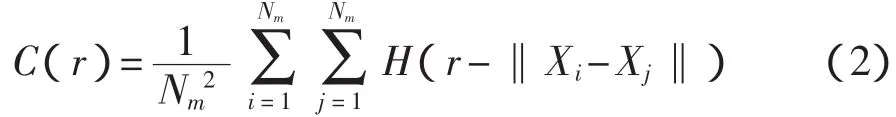
式中:i≠j;
C(r)——信號的相關積分(關聯函數);
H——Heaviside函數,當u≥0時,H(u)=1,當u<0 時,H(u)=0;
r——相空間中超球半徑。
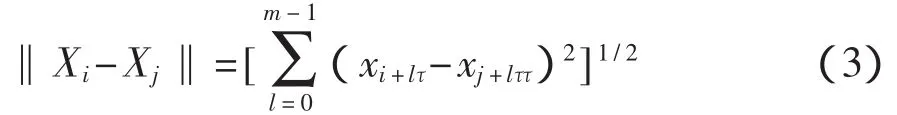
相關積分C(r)含義是嵌入空間中距離≤r的向量對出現的概率,且有

式中:D2——關聯維數,可由式(5)求出

1.2 參數的選取
1.2.1 延遲時間的選取
實際運用中延遲時間τ的選取對重構質量的好壞有極大影響。如果 τ太小,相空間 xn+jτ和 xn+(j+1)τ的坐標差別極小,運動軌跡總是在對角線附近,攜帶了大量的冗余信息;反之τ太大,坐標之間又變得獨立無關,特別是對于非線性混沌運動,任何微小的差異都會隨時間演化而越來越大,從而使得前后狀態完全無關[5]。在時間序列相空間重構中,延遲時間的算法主要有自相關函數法和互信息法兩大類。
1.2.2 嵌入維數的選擇
在重構相空間時,Takens定理提供了嵌入維數m的下限,即嵌入維數m≥2d+1(其中d為吸引子的真實維數)。由于無法獲得吸引子的真實維數,嵌入維數的下限也很難得出;因此,在研究中應盡量選擇大的嵌入維數,以滿足m≥2d+1。但嵌入維數過大,會增加計算量,且多余的相空間維數會放大原時間序列中噪聲的效應;而嵌入維數太小,動力系統的幾何結構不能完全打開。現有的許多選擇m的方法,如奇異值分解[6]、偽相圖法[7]等,其各有利弊。
1.2.3 超球半徑的選擇
超球半徑r的取值范圍首先應滿足條件:

式中:lmin=min(‖Xi-Xj‖);
lmax=max(‖Xi-Xj‖);
i,j=1,2,…,Nm,i≠j。
如果r取得太大,則任何一對矢量都發生“關聯”,此時C(r)=1;如果r取的太小,則任何一對矢量都不“關聯”,此時C(r)=0。兩種情況下的r都不能客觀反映系統的內在特質,所以必須適當地選擇r,使其在某個區間內滿足式(4),使關聯維數能客觀描述自相似結構的混沌吸引子特征。
1.3 無標度區的確定
自然界大量存在的隨機分形,它們只是在一定的尺度范圍(即無標度區)內具有分形特性。可以采用作圖法找出無標度區并計算分形維數(關聯維數),如根據lnr-lnC(r)圖求取信號的分維數值。此外,目前還發展了多種求取無標度區和分維數的其他算法,如三折線法[8]、遺傳算法[9]和自適應方法[10]等。
2 液壓閥數學模型的建立
液壓閥作為自動舵的執行機構舵機的控制部分,其作用是根椐放大器輸出的轉舵信號控制液壓油路的斷通和流向,從而確定舵機液缸活塞的運動方向。
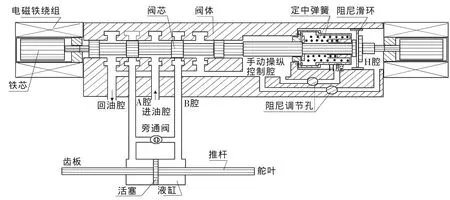
圖1 CDF-100液壓閥結構原理圖
圖1為CDF-100液壓閥結構原理圖,是由閥芯和閥體兩部分組成的三位四通電磁換向閥。通過對液壓閥的電路、磁路及受力進行分析,可建立其數學模型,有
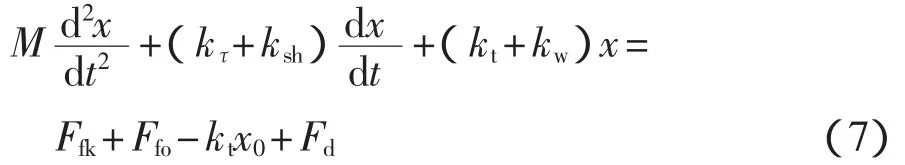
式中:M——閥芯質量;
x——閥芯位移;、
t——時間;
kτ——粘性阻尼系數;
ksh——瞬態液動力系數;
kt——彈簧剛度;
kw——穩態液動力剛度;
Ffk——卡緊摩擦力;
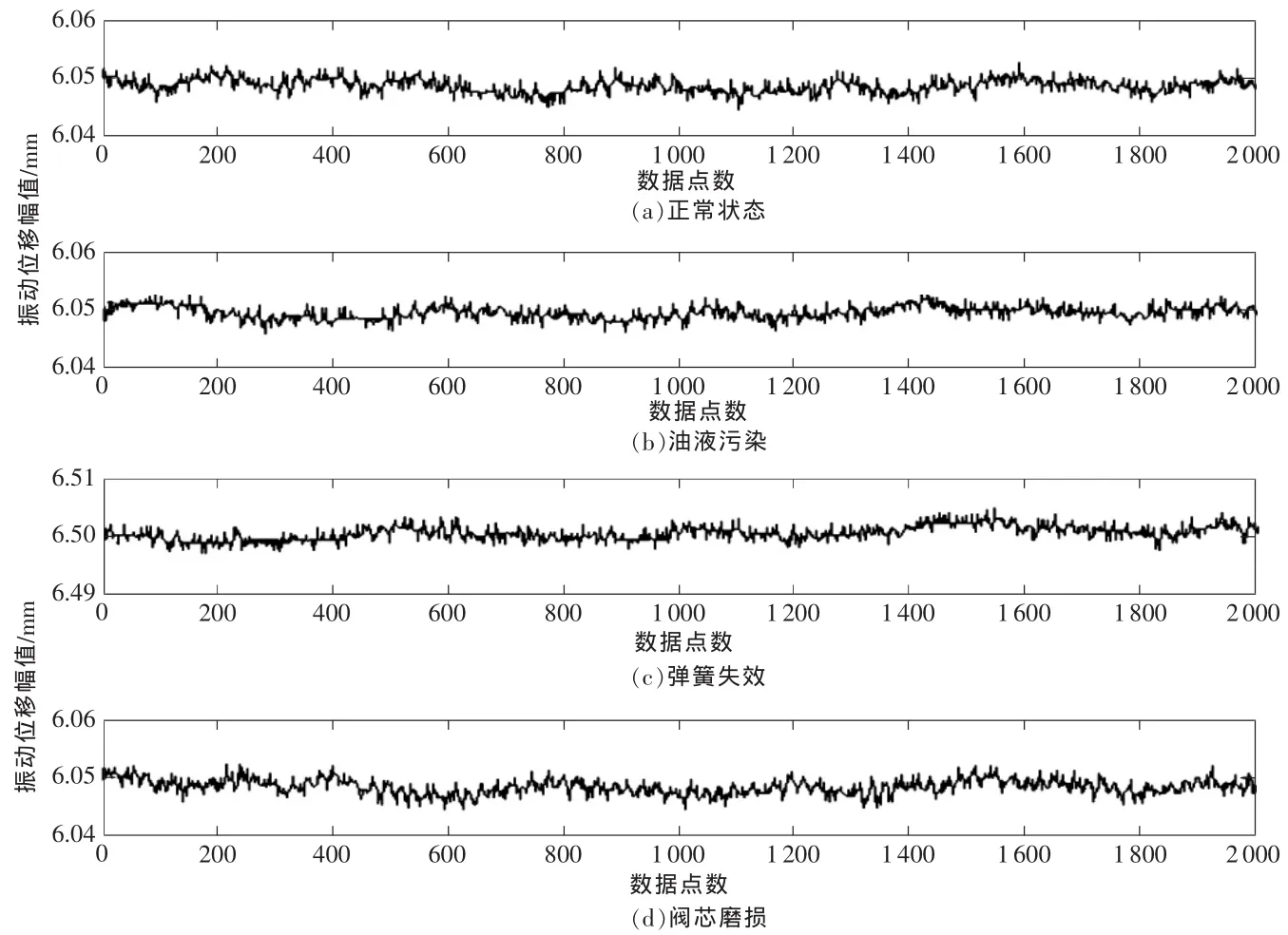
圖2 液壓閥4種狀態下閥芯的振動信號
Ffo——O型密封圈的摩擦力;
x0——復位彈簧預壓縮量;
Fd——電磁力。
3 液壓閥故障診斷實例分析
使用Matlab/Simulink對CDF-100液壓閥正常和3種故障(油液污染、彈簧失效和閥芯磨損)進行仿真實驗,采用四階Runger-Kutta算法,仿真步長0.0001s,仿真時間0.5 s,得到液壓閥換向過程中閥芯位移振動數據5 001個點,除去前3 001個瞬態點,取后2000點進行時間序列分析,如圖2所示。
圖2中(a)~(d)都反映了液壓閥工作過程中閥芯微動的存在,其中彈簧失效故障是指由于彈簧的失效使得閥芯的平衡位置發生改變,振動機理也有所改變,其他兩個故障在平衡位置上沒有發生變化,只是在振動機理上的改變。
本文采用自相關函數法來選取時間延遲τ,取自相關函數值降到初始值的1-1/e時的τ值為最佳時間延遲。如圖3所示,圖中與x軸平行貫穿始末的直線為初始值的1-1/e。
由圖3可知,液壓閥4種狀態下閥芯的振動信號的最佳延遲時間τ值分別如表1所示。
對于時間序列,利用先前確定的最佳時間延遲,給定一個嵌入維數,進行相空間重構,計算其關聯函數,畫出關聯積分曲線。在關聯積分曲線圖上,擬合其中線性度最好的區間,則該區間擬合直線的斜率就是該嵌入維數下的關聯維數。然后增加嵌入維數,用同樣的方法在關聯積分曲線圖上計算關聯維數,直到關聯維數不再隨嵌入維數的增加而增加,而是在一定誤差范圍內變化為止,此時的關聯維數就是該時間序列的關聯維數。圖4為不同的嵌入維數所對應的關聯積分曲線,圖5為關聯維數隨嵌入維數的變化關系,表2為關聯維數隨嵌入維數的變化關系的數據顯示。
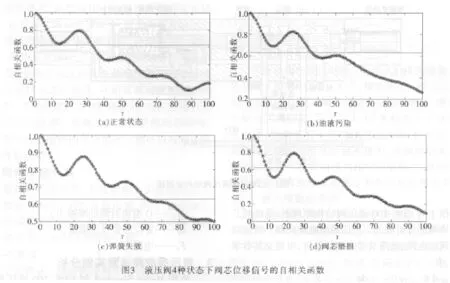

表1 液壓閥4種狀態下閥芯振動信號的最佳延遲時間
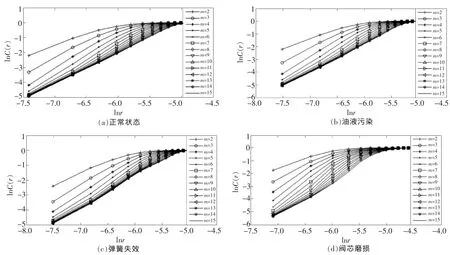
圖4 液壓閥4種狀態下閥芯位移信號的關聯積分曲線
由圖5和表2可知,4種工作狀態下當閥芯振動的位移信號隨著嵌入維數的增加,其關聯維數也增加。但當嵌入維數大于一定值時,關聯維數不再隨嵌入維數的增加而增加,而是在一定誤差范圍內變化。當嵌入維數m分別≥11,9,11和12時,關聯維數分別趨于穩定值 d=2.08,2.30,2.55,3.73,滿足嵌入定理m≥2d+1。分別取最小嵌入維數11,9,11和12,它標志系統有效自由度的數目,得4種工作狀態下閥芯振動位移信號的關聯維數2.08,2.30,2.55和3.73。可以看出,該型液壓閥閥芯振動信號在一定的尺度范圍內具有分形特征,不同的工作狀態對應不同的分形維數,而且具有明顯可分性,分形維數可以代表不同的工作狀態(故障)。因此,可以把關聯維數為2.08代表正常狀態,2.30代表油液污染故障,2.55代表彈簧失效故障,3.73代表閥芯磨損故障。實際應用中,采集液壓閥閥芯位移信號,計算其關聯維數值,若關聯維數值在 2.08,2.30,2.55,3.73附近時,則液壓閥對應于正常狀態、油液污染、彈簧失效和閥芯磨損狀態。
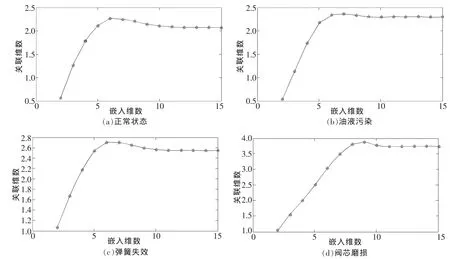
圖5 關聯維數隨嵌入維數的變化曲線
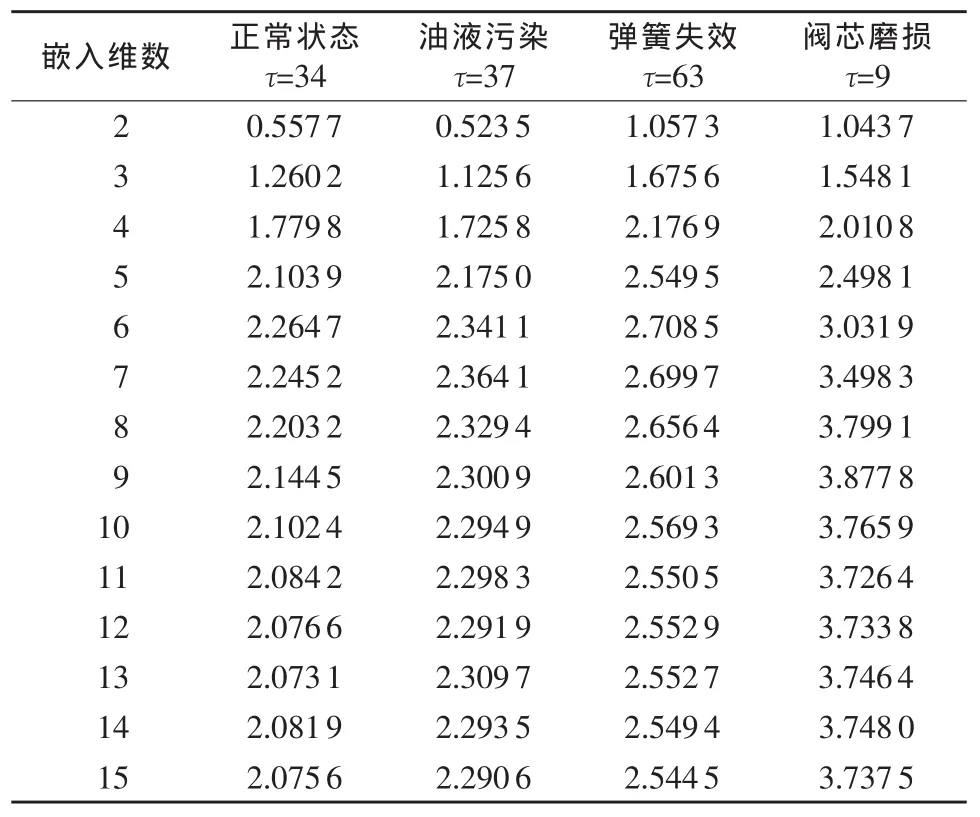
表2 不同嵌入維數下的關聯維數
4 結束語
本文利用分形理論,通過計算液壓閥閥芯位移信號的關聯維數,對液壓閥的不同工作狀態進行了定量描述,并以此為依據實現了對不同液壓閥故障的診斷。研究結果表明,該方法直接、簡潔、方便,克服了傳統方法在故障信號特征提取和分析上的困難,具有良好的實際應用價值。
[1]呂金虎,陸君安,陳士華.混沌時間序列分析及其應用[M].武漢:武漢大學出版社,2002:2-71.
[2]徐玉秀,原培新,楊文平.復雜機械故障診斷的分形與小波方法[M].北京:機械工業出版社,2003:1-45.
[3]李偉,李天偉,王桂軍,等.分形特征的模擬電路故障診斷方法[J].中國測試,2010,36(2):14-17.
[4]詹亮,劉瀏.基于分形維數的火焰特征提取方法[J].西華大學學報:自然科學版,2009,28(5):45-47.
[5]張菁,樊養余,李慧敏,等.相空間重構中延遲時間選取的新算法[J].計算物理,2011,28(3):469-474.
[6]王浩,張來斌,王朝暉,等.迭代奇異值分解降噪與關聯維數在煙氣輪機故障診斷中的應用[J].中國石油大學學報,2009,33(1):93-98.
[7]于慶江.分形方法在往復壓縮機狀態監測與故障診斷上的應用[D].大慶:大慶石油學院,2007:12-36.
[8]李厚強,汪富泉.分形理論及其在分子科學中的應用[M].北京:科學出版社,1997:23-68.
[9]費斌,蔣莊德,王海容.基于遺傳算法求解分形無標度區的方法[J].西安交通大學學報,1998,32(7):72-75.
[10]巫兆聰.分形分析中的無標度區確定問題[J].測繪學報,2002,31(3):240-244.

