IPM磁鋼參數(shù)及隔磁槽對感應(yīng)電勢的影響
翟秀果,劉慧娟
(北京交通大學(xué),北京100044)
0 引 言
內(nèi)嵌式永磁同步電機(jī)永磁體尺寸的選取一方面影響永磁材料的利用率,另一方面影響定子繞組感應(yīng)電勢和漏磁系數(shù)等物理量,進(jìn)而會影響電機(jī)的調(diào)速和控制,所以對磁極的優(yōu)化顯得尤為重要,永磁體結(jié)構(gòu)參數(shù)的優(yōu)化包括對極弧系數(shù)[1]、永磁體寬度和厚度三種參數(shù)的優(yōu)化設(shè)計。
國內(nèi)外關(guān)于永磁電機(jī)這三種參數(shù)優(yōu)化方面的研究主要是對其中一個參數(shù)或兩個參數(shù)的優(yōu)化,沒有對三個參數(shù)同時進(jìn)行優(yōu)化的研究,特別對于內(nèi)嵌式永磁同步電機(jī),永磁體結(jié)構(gòu)參數(shù)的優(yōu)化設(shè)計對電機(jī)感應(yīng)電勢波形及其諧波總量的影響,以及隔磁橋?qū)β┐畔禂?shù)的影響的研究顯得格外重要。
本文首先利用Ansoft Maxwell軟件對8極內(nèi)嵌式永磁同步電機(jī)[2]進(jìn)行建模,在瞬態(tài)模型中仿真V字形磁鋼三種結(jié)構(gòu)參數(shù)變化對定子繞組感應(yīng)電勢波形的影響[3],計算感應(yīng)電勢波形的諧波總量(THD),繪制出三種參數(shù)變化與感應(yīng)電勢幅值和諧波含量(THD)值變化的關(guān)系圖,從而得到獲得最大感應(yīng)電勢幅值和最小THD值的永磁體結(jié)構(gòu)參數(shù)的最優(yōu)值。在永磁體的三個參數(shù)中,永磁體寬度W和厚度T的變化易于實現(xiàn),而極弧系數(shù)用V字形磁鋼的夾角θ來表示。同步電機(jī)的極弧系數(shù)定義為氣隙平均磁密與最大磁密的比值,如:
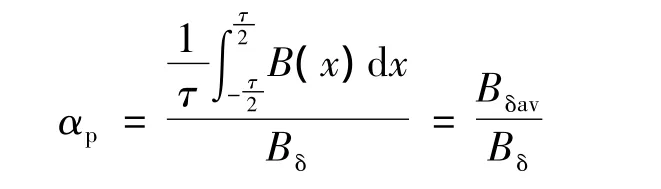
式中:B(x)為氣隙磁密沿氣隙圓周展開長的分布波形;Bδav為氣隙平均磁密;Bδ為氣隙最大磁密;τ為永磁極沿氣隙圓周展開長的極距[2]。對于圖1的內(nèi)嵌V字型永磁電機(jī),影響B(tài)δav的主要是V字型的張開角度。
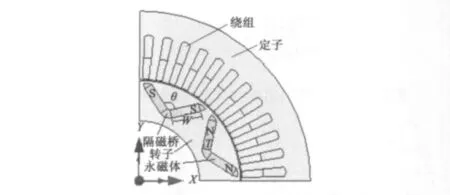
圖1 V字形內(nèi)嵌式永磁同步電機(jī)模型
然后空載穩(wěn)態(tài)下仿真不同永磁體槽形狀對感應(yīng)電勢幅值的影響,并測得磁鋼外端部上磁矢量位[3]Az1和定子槽外圓弧段上磁矢量位Az2,計算漏磁系數(shù),進(jìn)而得出最小漏磁條件下的永磁體槽設(shè)計。
1 電機(jī)模型
8極內(nèi)嵌式永磁同步輪轂電機(jī)模型的具體參數(shù)如表1所示。

表1 永磁同步電機(jī)參數(shù)
為了節(jié)省軟件仿真計算時間,給出電機(jī)的1/4模型,如圖1所示,其中轉(zhuǎn)子由轉(zhuǎn)子鐵心、永磁體和隔磁橋三部分構(gòu)成。
2 三種結(jié)構(gòu)參數(shù)對感應(yīng)電勢的影響
Maxwell 2D瞬態(tài)求解器下建立電機(jī)模型之后,計算開路狀態(tài)下定子繞組的感應(yīng)電勢波形。
2.1 極弧系數(shù)對感應(yīng)電勢的影響
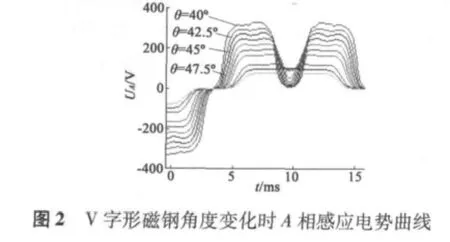
保持磁鋼寬度值W=15 mm和厚度值T=4.5 mm不變,設(shè)置V形磁鋼夾角θ為變量參數(shù),變化范圍從80°~140°,計算步長為6°,對模型進(jìn)行參數(shù)化分析,得到感應(yīng)電勢曲線如圖2所示。V型磁鋼夾角80°時有最大感應(yīng)電勢幅值394.15 V,夾角105°時幅值最小為225 V。
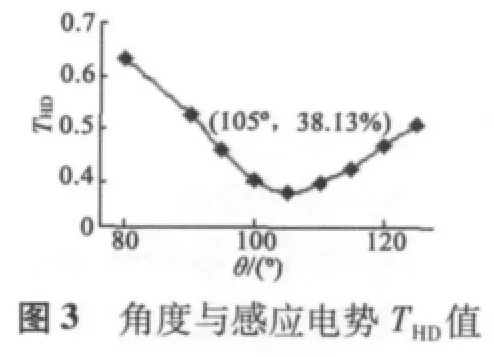
圖2中角度不僅影響感應(yīng)電勢的幅值,也影響其波形,感應(yīng)電勢THD值越小,其波形越接近正弦波,用快速傅里葉變換法(FFT)計算得到各波形THD值和基波值,并繪制出關(guān)于各參數(shù)的曲線圖。當(dāng)THD值最小時,便得到最優(yōu)的正弦波感應(yīng)電勢。圖3為V形角度變化時感應(yīng)電勢THD值變化曲線,THD值隨角度的增大先減小再增大,角度為105°時取得最小THD值38.13%。圖4為V形角度變化時感應(yīng)電勢基波值變化條形圖,基波值隨角度增大而單調(diào)減小。

2.2 磁鋼寬度對感應(yīng)電勢的影響
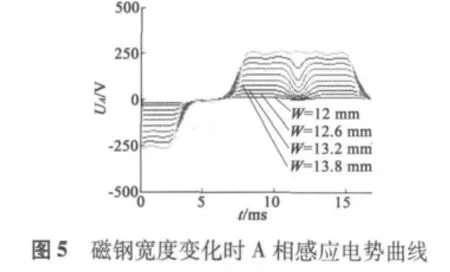
保持磁鋼角度θ=105°和厚度值T=4.5 mm不變,設(shè)置磁鋼寬度W為變量參數(shù),變化范圍從12~18 mm,取步長為0.6 mm,對模型進(jìn)行參數(shù)化分析,得到感應(yīng)電勢曲線如圖5所示,感應(yīng)電勢隨磁鋼寬度增大而增大,W=12 mm時感應(yīng)電勢幅值最小為30 V;W=18 mm時感應(yīng)電勢幅值最大為266 V。
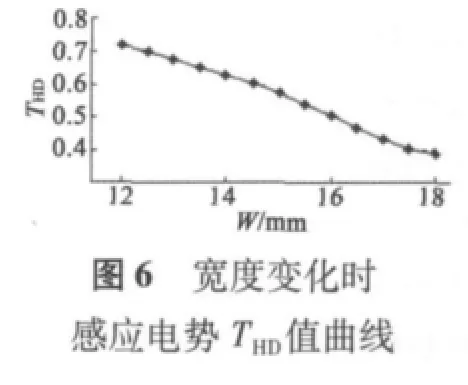
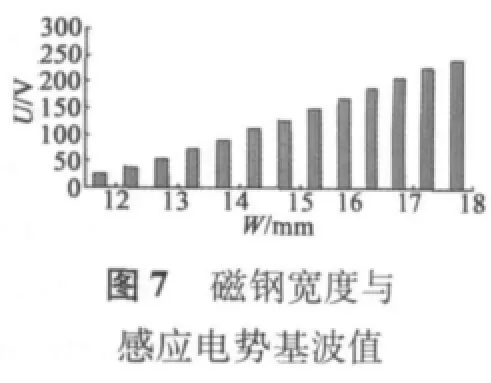
圖6為磁鋼寬度變化時感應(yīng)電勢THD值曲線,THD值隨寬度的增大而減小;圖7為磁鋼寬度與感應(yīng)電勢基波值條形圖,可以看出,基波值隨寬度增加而單調(diào)增大。
2.3 磁鋼厚度對感應(yīng)電勢的影響
保持磁鋼角度θ=105°和寬度W=15 mm不變,設(shè)置磁鋼厚度T為變量參數(shù),變化范圍從3~7.5 mm,步長設(shè)為0.45 mm,對模型進(jìn)行參數(shù)化分析,感應(yīng)電勢曲線如圖8所示,10條感應(yīng)電勢曲線重合在一起,說明厚度值T不影響感應(yīng)電勢曲線波形,因為永磁體采用厚度方向上的平行充磁。
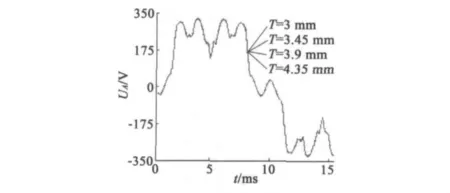
圖8 磁鋼厚度變化時A相感應(yīng)電勢曲線
2.4 永磁體三個結(jié)構(gòu)參數(shù)的關(guān)聯(lián)研究
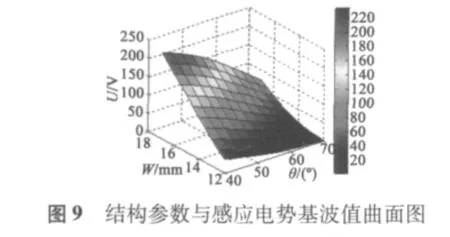
為了達(dá)到最優(yōu)參數(shù)設(shè)計,仿真三個參數(shù)同時變化時A相感應(yīng)電勢曲線圖,得出在寬度W=18 mm、角度θ=92°、厚度T=6.5 mm時有最大感應(yīng)電勢幅值470 V。因為厚度變化不影響感應(yīng)電勢波形,繪制關(guān)于THD和基波值圖形時只需考慮寬度和角度關(guān)聯(lián)變化的情況,其三維圖形如圖9和圖10所示。
圖9中θ軸代表角度變化,W軸代表寬度變化,縱軸代表感應(yīng)電勢基波幅值,當(dāng)磁鋼夾角增大和寬度減小時,基波值持續(xù)減小趨勢。
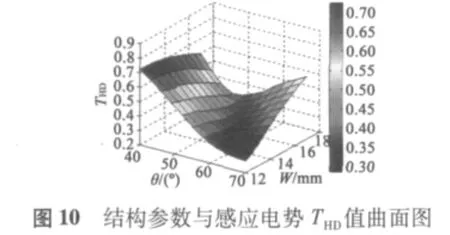
圖10中θ軸代表角度變化,W軸代表寬度變化,縱軸代表感應(yīng)電勢THD值,在W=-0.25θ+40處有最小THD值,約為35%。
3 永磁體隔磁橋形狀對電機(jī)漏磁系數(shù)的影響
本文內(nèi)嵌式永磁同步電機(jī)的磁力線分布如圖11所示,磁鋼端部和氣隙之間的隔磁槽形狀影響磁力線的分布,將圖11中C部分放大到圖12中,進(jìn)行四種不同槽形磁力線分布的比較。圖12中(a)為不設(shè)置端部隔磁槽,此時有2條磁力線未與定子繞組交鏈;(b)為設(shè)計了小尺寸三角狀隔磁槽,槽端部與氣隙間距離b=1 mm,此時有1條磁力線未與定子繞組交鏈;(c)為b=0.5 mm時槽的形狀,磁力線都與定子繞組交鏈;(d)為b=0即槽與氣隙連通時的槽形,磁力線都與定子繞組交鏈。
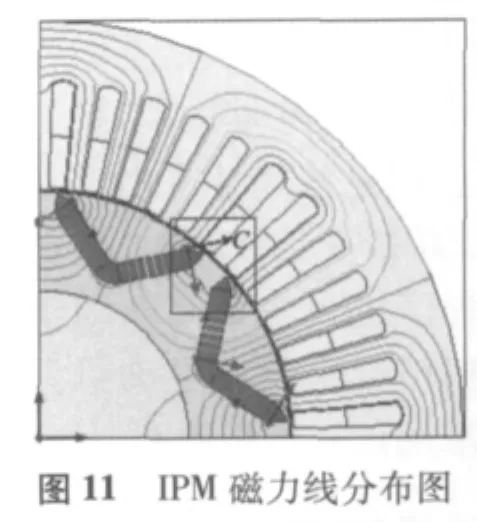
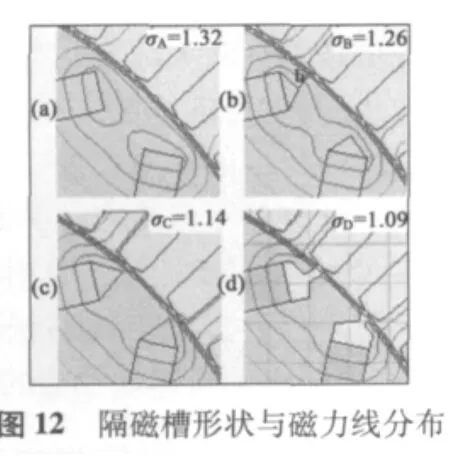
圖13揭示了四種槽形對定子感應(yīng)電勢的影響,感應(yīng)電勢幅值單調(diào)增加,波形變尖。
磁力線分布圖和感應(yīng)電勢幅值的比較都從側(cè)面反映了四種槽形設(shè)計的漏磁規(guī)律,計算漏磁系數(shù)可以更準(zhǔn)確地比較四種設(shè)計的漏磁情況。
提取出永磁體外端部上的磁矢量位Az1和定子繞組外側(cè)圓弧上的磁矢量位Az2的數(shù)據(jù)表,Az1代表總磁通Φm的單位磁通量,Az2代表主磁通Φδ的單位磁通量[8],所以電機(jī)的空載漏磁系數(shù)用磁矢量位表示,計算得出σA=1.32,σB=1.26,σC=1.14,σD=1.09,說明從(a)到(d)四種設(shè)計漏磁系數(shù)單調(diào)減小,永磁體利用率越來越高。

圖13 不同槽形的感應(yīng)電勢曲線
4 結(jié) 論
通過對內(nèi)嵌式永磁同步電機(jī)三種參數(shù)對感應(yīng)電勢的影響以及隔磁槽形狀對漏磁系數(shù)影響的研究,得出以下結(jié)論:
(1)在磁鋼寬度W=18 mm,角度θ=92°,厚度T=6.5 mm時有最大感應(yīng)電勢幅值470 V;磁鋼厚度變化不影響感應(yīng)電勢波形;角度增大時THD值先減小再增大,并在105°時取最小值,寬度增大時THD值單調(diào)減小;寬度和角度關(guān)聯(lián)時,在W=-0.25θ+40處有最小THD值,約為35%。
(2)隔磁槽形狀設(shè)計中,b值越小,漏磁系數(shù)越小,當(dāng)b=0時,有最小的漏磁系數(shù),b=1.09。
[1] Bose B K.A high-perforomance inverter-fed drive system of an Interior permanent magnet synchronous machine[J].IEEE Transactions on Industry Applications,1988,24(6):987-997.
[2] Jahms Thomas M.Flux weakening regime operation of an Interior permanent magnet synchronous motor drive[J].IEEE Transactions on Industrial Application,1987,23(4):681-689.
[3] 田淳.無位置傳感器同步電機(jī)直接轉(zhuǎn)矩控制的理論研究與實踐[D].南京航空航天大學(xué),2001.
[4] 唐任遠(yuǎn).現(xiàn)代永磁電機(jī)理論與設(shè)計[M].北京:機(jī)械工業(yè)出版社,1997.
[5] Fraiz J,Mohseni-Zonoozi S H.A novel technique for estimation and control of stator flux of a salient-pole PMSM in DTC method based on MTPF[J].IEEE Transactions on Industrial Electronics,2003,50(2):262-271.
[6] Mellor P H,Chaaban F B.Estimation of parameters and performance of rare earth permanent magnet motors a voiding measurement of load angle[J].IEE Proceedings on Electric Power Application,1991,138(6):322-330.

