形變映射法及其在BBM方程中的求解應用

王 慶

(遼寧對外經貿學院基礎課教學部，遼寧 大連 116052)

形變映射法及其在BBM方程中的求解應用

王 慶

(遼寧對外經貿學院基礎課教學部，遼寧 大連 116052)

形變映射法在求解非線性方程的過程中起著重要作用，借助于計算機代數幾何系統，不僅得到了一類非線性波動方程與非線性Klein?Gordon(NKG)方程特殊類型解之間的代數映射關系，而且由此給出BBM方程的許多顯示精確解。并且由這些解再次映射出了諸多行波解，在物理學的研究方面具有重要的指導意義。

形變映射法；BBM方程；非線性Klein?Gordon(NKG)方程

近年來,人們對非線性問題的研究逐步升溫, 非線性問題涉及到自然科學和社會科學的諸多領域。但要得到描述這種關系的非線性演化方程的精確函數卻并不容易。隨著數學和計算機代數幾何系統的巨大發展,非線性演化方程的許多新的求解方法不斷應運而生,如Jacobi橢圓函數展開法[1]、雙曲函數法、李對稱群變換法、形變映射法、Darboux變換法、Backlund變換法、反散射法、齊次平衡法、對稱約化法[2]等。各種求解方法都有其各自的特點和優勢，而形變映射法在求解非線性發展方程中，解法簡便靈活，解的形式多樣，深受學習者的偏愛。其基本思想是通過建立與所給的非線性方程同已知的線性或非線性方程及其解之間的代數映射關系,從而獲得所求的非線性方程的解。通過形變映射法針對BBM方程求解,它的最大優點是能夠給出更多的顯式精確解。下面，筆者對形變映射法及其在BBM方程中的求解應用進行了研究。

1 形變映射法

我國著名科學家樓森岳先生在20世紀80年代首先提出了形變映射法[3],他通過建立三次非線性Klein-Gordon(NKG)方程得到了代數映射關系，從而可以獲得非線性偏微分方程豐富的新的顯示精確行波解[4]，包括孤子解、周期波解、雅可比橢圓函數解以及其他一些精確解。具體步驟如下：

(i)假定非線性物理方程：

F(x,t,u,ut,ux,uxx,…)=0

(1)

具有如下的形波解u(x,t)=u(ξ)，ξ=k(x-ct)，其中，k，c為待定常數。則方程(1)可以轉化為關于u(ξ)的非線性常微分方程：

F(u,uξ,uξξ,…)=0

(2)

(ii)引入中間函數Φ=Φ(ξ)，滿足非線性Klein-Gordon方程：

(3)

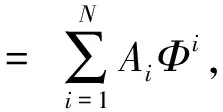
2 BBM方程的求解

Benjamin、Bona和Mahony研究表明[1]，Kdv方程作為流體當中長波單向傳播的模型方程是有缺點的，進而提出了另一個更合適的非線性色散介質中長波單向傳播模型方程即BBM方程：

ut+ux+uxt+αuxxt=0

取代了Kdv方程，這類方程還出現在其他許多數學物理問題中。在文獻[5]中，三次非線性NKG方程的許多精確解已經給出。下面，筆者利用代數變換關系u=a0+a1φ2得到BBM方程多種類型的顯式精確解，如孤波解、周期波解、Jacobi橢圓函數解等。

首先，對BBM方程作行波約化：

u(x,t)=U(ξ)ξ=k(x-ct)

(4)

式中，k為波數；c為波速。將式(4)代入BBM方程，得到下面的常微分方程：

(1-c)U′+UU′-αck2U?=0

(5)

式(5)兩邊對ξ積分一次，得：

(6)

式中，A為積分常數。建立代數變換關系：

u(x,t)=U(ξ)=U(φ(ξ))=a0+a1φ2

(7)

式中，a1為待定常數，φ=φ(ξ)為三次非線性NGK方程：

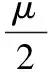
(8)

的解，b，λ，μ是常數，ξ=k(x-ct)。

將式(7)和式(8)代入方程(6)，得到：

(9)

令式(9)中φi(i=0,2,4)項前面的系數為零，得到：

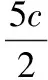
(10)

式中，α,b,c,k,λ,μ均為任意常數。根據文獻[5]就可以得到BBM方程一系列解,其中大部分解與前面所求的解形式一樣，下面只列出新形式的橢圓函數解。

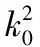
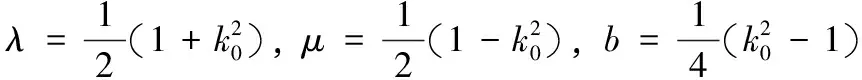
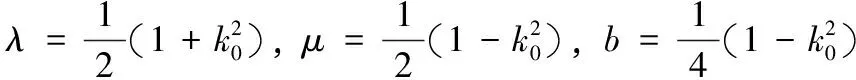
這樣就得到了BBM方程的新的復合形式的橢圓函數解。

3 結 語

運用形變映射法建立三次非線性Klein-Gordon(NKG)方程，解得代數映射關系，得到了一類Kdv方程(6)豐富的新的顯示精確行波解，包括孤波解、周期波解、雅可比橢圓函數解和其他一些精確解。當然，這只是在非線性方程的求解方法做出了一點嘗試，求解非線性方程有很大難度，為尋求更一般的更有普遍意義求解方法還需要更多的努力。

[1]李德生,張鴻慶.非線性演化方程橢圓函數解得一種簡單求法及其應用[J].物理學報,2006,55:1565-1570.

[2]谷超豪.孤立子理論與應用[M].杭州：浙江科技出版社，1990:176-215.

[3] Lou S Y,Ni G J.The relations among a special type of solutions in some (D+1)-dimensional nonlinear equations[J].J Math Phys,1989,30:1614.

[4]傅海明,戴正德.一類Kdv方程的孤波解[J].寧夏師范學院學報,2009,30(3):1-4.

[5]范恩貴.可積系統與計算機代數[M].北京:科學出版社,2003.

[編輯] 洪云飛

10.3969/j.issn.1673-1409(N).2012.11.004

O175 2

A

16731409(2012)11N01002