儲(chǔ)罐液體晃蕩問(wèn)題的有限元分析

賈善坡，趙友清，許成祥 朱成安 譚繼可

(長(zhǎng)江大學(xué)城市建設(shè)學(xué)院，湖北 荊州 434023)(中石油唐山液化天然氣項(xiàng)目經(jīng)理部，河北 唐山 063000)(長(zhǎng)江大學(xué)城市建設(shè)學(xué)院，湖北 荊州 434023)

儲(chǔ)罐液體晃蕩問(wèn)題的有限元分析

賈善坡，趙友清，許成祥 朱成安 譚繼可

(長(zhǎng)江大學(xué)城市建設(shè)學(xué)院，湖北 荊州 434023)(中石油唐山液化天然氣項(xiàng)目經(jīng)理部，河北 唐山 063000)(長(zhǎng)江大學(xué)城市建設(shè)學(xué)院，湖北 荊州 434023)

采用有限元方法數(shù)值求解了任意容器內(nèi)液體晃動(dòng)的固有頻率、模態(tài)和地震響應(yīng)動(dòng)力學(xué)問(wèn)題。基于液體晃動(dòng)的泛函極值原理，在晃動(dòng)自由面上忽略液體的表面張力，對(duì)液體晃動(dòng)有限元方程進(jìn)行靜態(tài)縮聚，計(jì)算了矩形容器內(nèi)液體晃動(dòng)的特征頻率，并與解析解進(jìn)行比較。研究表明，利用該方法計(jì)算的結(jié)果具有較高精確度，可以為研究?jī)?chǔ)罐晃動(dòng)動(dòng)力特性分析提供參考。

液體晃動(dòng)；有限元法；充液容器；地震響應(yīng)

晃蕩是指部分充滿液體的容器在外部激振力的作用下產(chǎn)生可自由移動(dòng)的自由表面的現(xiàn)象，它是一種非常復(fù)雜的流體運(yùn)動(dòng)，呈現(xiàn)出很強(qiáng)的非線性和隨機(jī)性。液體的晃動(dòng)問(wèn)題在石油化工設(shè)備、高層建筑減振、城市供水、船舶等領(lǐng)域均有應(yīng)用，具有廣泛的工程背景[1-2]。儲(chǔ)罐、液體儲(chǔ)槽及水塔等地面設(shè)備在地震中由于內(nèi)部所儲(chǔ)存液體的劇烈晃動(dòng)而遭破壞；在罐裝汽車行業(yè)中，必須要對(duì)液化氣體、石油、化學(xué)劑等的大型液體運(yùn)輸罐進(jìn)行晃動(dòng)分析；在船舶工程領(lǐng)域，船舶被用來(lái)運(yùn)輸大量液體，大體積液體的晃動(dòng)對(duì)船舶結(jié)構(gòu)穩(wěn)定性的影響尤為突出[3]。容器液體晃動(dòng)和控制問(wèn)題的研究受到眾多研究人員的廣泛重視，李遇春等[5]利用邊界元方法對(duì)液體非線性晃動(dòng)問(wèn)題進(jìn)行了數(shù)值分析；包光偉等[6]采用VOF方法對(duì)液體晃動(dòng)進(jìn)行了數(shù)值仿真；周宏等[7]采用ALE方法對(duì)帶有自由液面的晃動(dòng)問(wèn)題進(jìn)行了分析討論；尚春雨等[8]提出用FLUENT計(jì)算液體晃動(dòng)問(wèn)題的方法；李青等[9]推導(dǎo)了任意三維貯箱內(nèi)液體晃動(dòng)的等效力學(xué)模型，采用有限元方法建立計(jì)算等效力學(xué)模型參數(shù)的數(shù)值算法，并采用商用分析軟件FLOW-3D 驗(yàn)證了等效力學(xué)模型的有效性。下面，筆者基于液體晃動(dòng)的泛函極值原理，采用靜態(tài)縮聚技術(shù)，進(jìn)而提出了儲(chǔ)罐流體晃動(dòng)特征問(wèn)題的有限元計(jì)算方法。

1 基本方程

將儲(chǔ)罐容器壁簡(jiǎn)化為剛性，把儲(chǔ)液看成無(wú)旋和不可壓縮流體，則液體在域V內(nèi)滿足連續(xù)性方程和Euler水動(dòng)力學(xué)方程，在容器濕表面?Vw(固壁邊界)上滿足不可滲透性條件，在自由面?Vf(自由面邊界)上滿足運(yùn)動(dòng)學(xué)邊界條件和動(dòng)力學(xué)邊界條件。設(shè)液體的速度勢(shì)為Φ(x,y,z)，則Φ液體在域V滿足如下方程[10]：

▽2Φ(x,y,z)=0

(1)

在容器壁面和自由表面上滿足的邊界條件如下：

(2)

式中，g是重力加速度；?Vw、?Vf分別是壁面邊界、自由面邊界。

令Φ(x,y,z)=iωφ(x,y,z)eiωt，代入式(1)和式(2)，構(gòu)造如下泛函：

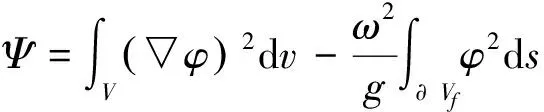
(3)

將液體域V上的解函數(shù)寫成如下形式：

(4)

式中，Nj(x,y,z)為流體單元形函數(shù)；φj為單元節(jié)點(diǎn)變量。

將式(4)代入泛函表達(dá)式(3)，則泛函成為節(jié)點(diǎn)變量(φ1,φ2,…,φn)的函數(shù)，即：

Ψ=Ψ(φ1,φ2,…,φn)

(5)

求解泛函極值問(wèn)題等價(jià)于求解下列方程組

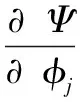
(6)

的解(φ1,φ2,…,φn)，從而確定液體域V上的解函數(shù)(4)。

2 液體晃動(dòng)問(wèn)題的有限元模型

液體晃動(dòng)的有限元方程為：

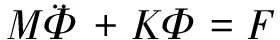
(7)

式中，Φ為液體節(jié)點(diǎn)速度勢(shì)陣；M為流體質(zhì)量陣；K為流體剛度陣；F為流體力矢量陣。

將Φ寫為Φ=[Φ1,Φ2]，其中，Φ1、Φ2分別對(duì)應(yīng)于自由液面節(jié)點(diǎn)和液體域節(jié)點(diǎn)，則式(7)可寫為：

(8)

對(duì)于液體晃動(dòng)問(wèn)題，系統(tǒng)的自由度相當(dāng)多，計(jì)算費(fèi)時(shí)且求解困難，因而采用靜態(tài)凝聚技術(shù)對(duì)流體晃動(dòng)計(jì)算問(wèn)題進(jìn)行簡(jiǎn)化[11-12]。

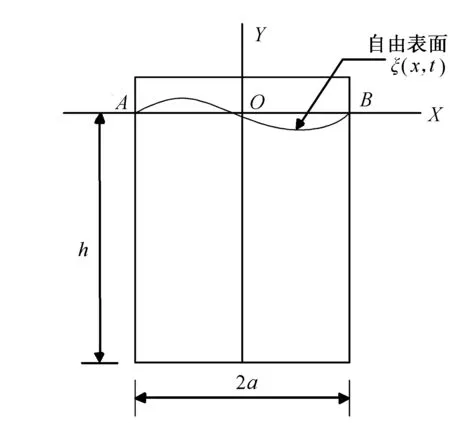
圖1 矩形容器示意圖

由式(7)可以發(fā)現(xiàn)，式(1)為拉普拉斯方程，對(duì)質(zhì)量陣M無(wú)貢獻(xiàn)，只有自由液面邊界條件對(duì)質(zhì)量陣M有貢獻(xiàn)，故M12=M22=0，而M11正是自由液面邊界條件對(duì)質(zhì)量陣的貢獻(xiàn)。對(duì)式(8)進(jìn)行靜態(tài)縮聚，可得到：

(9)

3 計(jì)算實(shí)例

選取二維矩形容器(見圖1)內(nèi)液體晃動(dòng)問(wèn)題作為計(jì)算實(shí)例，相關(guān)參數(shù)如下：容器寬度2a=3m，充液深度h=4m，液體密度ρ=1000kg/m3。

假定容器內(nèi)的液體是無(wú)旋和不可壓縮的，則液體晃動(dòng)的自然頻率解為[13]：

(10)

表1 有限元解與解析解的比較

3.1液體自由晃動(dòng)分析

液體自由晃動(dòng)分析的數(shù)值解和理論解如表1所示。從表1可以看出，流體晃動(dòng)前7階頻率的誤差一般控制在5%以內(nèi)，說(shuō)明利用該方法分析的誤差較小。

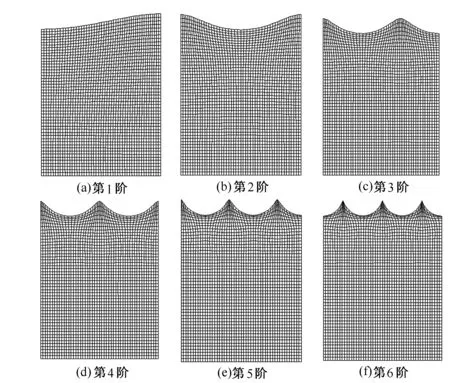
圖2 矩形容器前6階液體晃動(dòng)模態(tài)圖

3.2地震響應(yīng)分析

輸入El-Centro地震波，其最大峰值加速度為35×10-2m/s2，時(shí)間為40s，El-Centro地震波波形如圖3所示，液體在地震激勵(lì)El-Centro波作用下自由液面中點(diǎn)O的液面晃動(dòng)高度隨時(shí)間的反應(yīng)曲線如圖4所示(液體晃動(dòng)波高的數(shù)量級(jí)為10-8，接近于不晃動(dòng)狀態(tài))。

自由液面中點(diǎn)A處液面波高時(shí)程曲線如圖5所示。由圖5可知，在El-Centro地震荷載作用下，點(diǎn)A處液面的晃動(dòng)波高在t=12.78s時(shí)達(dá)最大值(0.120m)。自由液面中點(diǎn)B處液面波高時(shí)程曲線如圖6所示。由圖6可知，在t=5.37s時(shí)，點(diǎn)B處液面晃動(dòng)的最大波高為0.148m。同時(shí),可以看出，點(diǎn)A處與點(diǎn)B處的晃動(dòng)形態(tài)相反，并且液體晃動(dòng)具有明顯的非線性性能。

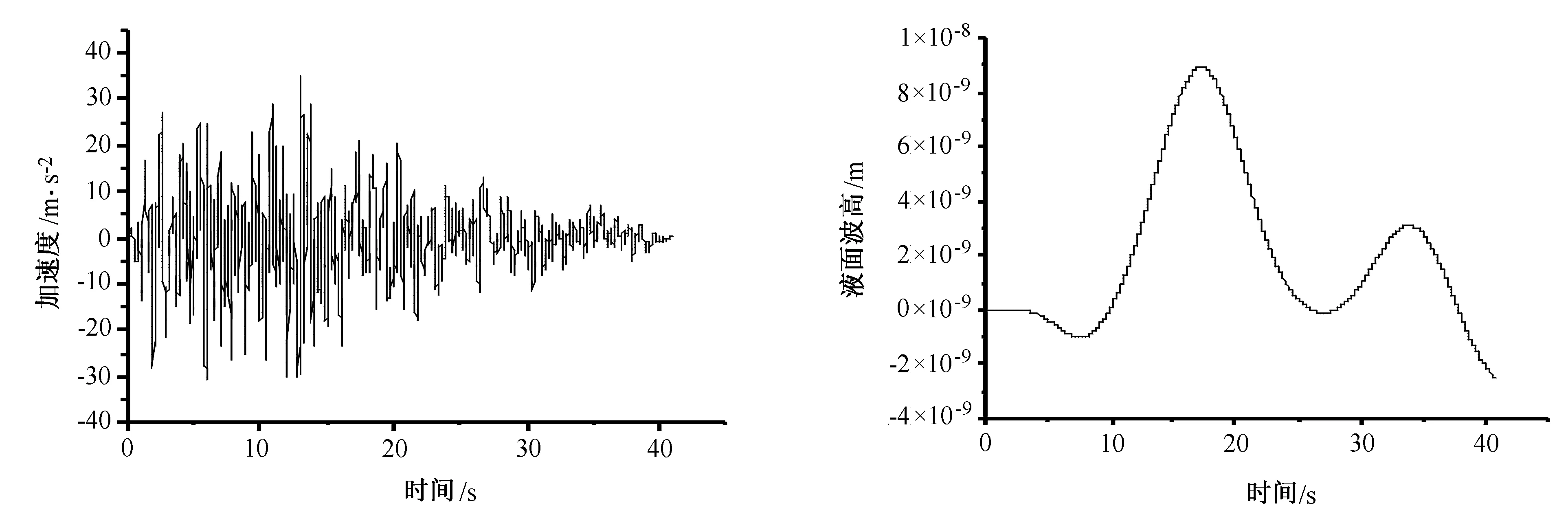
圖3 El-Centro地震波時(shí)程曲線 圖4 自由液面點(diǎn)O處液面波高時(shí)程曲線

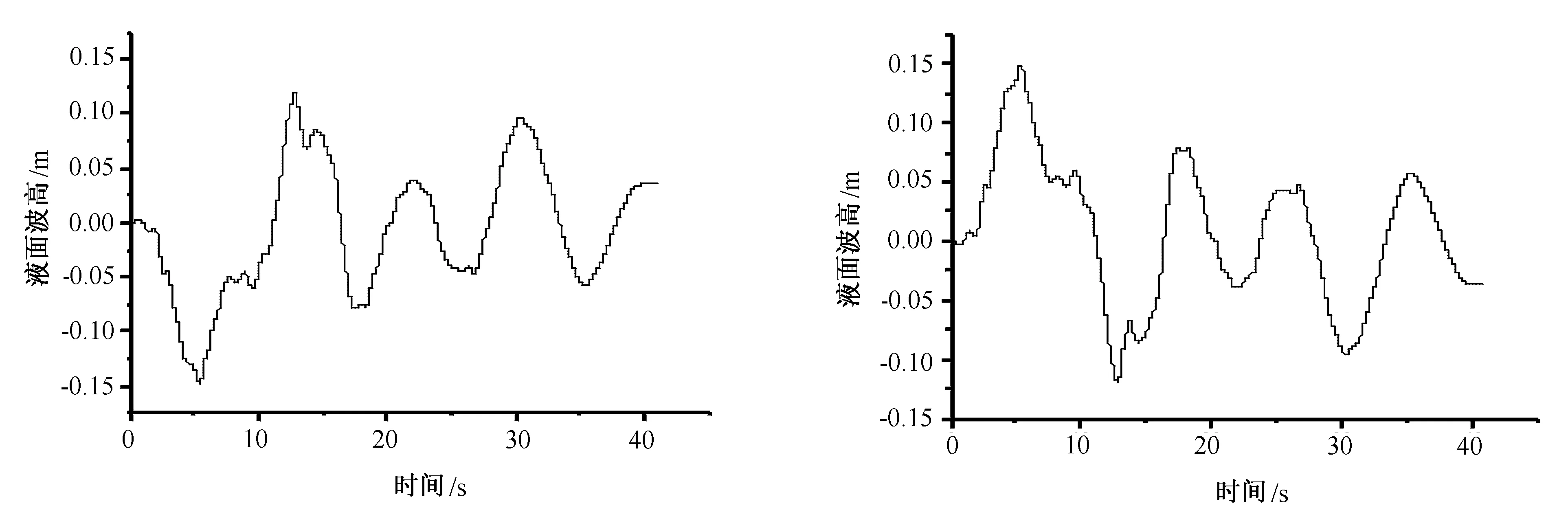
圖5 自由液面中點(diǎn)A處液面波高時(shí)程曲線 圖6 自由液面中點(diǎn)B處液面波高時(shí)程曲線

4 結(jié) 語(yǔ)

采用有限元法建立了任意充液容器內(nèi)液體晃動(dòng)問(wèn)題的數(shù)值計(jì)算方法，研究中假定容器壁面是剛性的，在晃動(dòng)自由面上忽略了液體的表面張力，采用靜態(tài)縮聚技術(shù)來(lái)了解容器內(nèi)液體的晃動(dòng)動(dòng)力特性，并通過(guò)算例驗(yàn)證了該方法的正確性。該方法可適于分析二維和三維等復(fù)雜形狀容器內(nèi)液體的晃動(dòng)問(wèn)題，但對(duì)流固耦合問(wèn)題，特別是抑制防晃問(wèn)題以及流體-儲(chǔ)罐-地基相互耦合問(wèn)題有待進(jìn)一步研究。

[1]賈善坡,許成祥.儲(chǔ)液容器內(nèi)液體自由晃動(dòng)的有限元分析[J].船舶力學(xué), 2012, 16(1-2):21-26.

[2]許成祥,賈善坡.儲(chǔ)罐結(jié)構(gòu)有限元?jiǎng)恿δＰ托拚皡?shù)辨識(shí)研究[J].武漢理工大學(xué)學(xué)報(bào),2010,32(9):286-290.

[3]岳寶增,祝樂(lè)梅,于丹.儲(chǔ)液罐動(dòng)力學(xué)與控制研究進(jìn)展[J].力學(xué)進(jìn)展, 2011,41(1):79-92.

[4]王照林，劉延柱.充液系統(tǒng)動(dòng)力學(xué)[M].北京:科學(xué)出版社，2002.

[5]李遇春,樓夢(mèng)麟.渡槽中流體非線性晃動(dòng)的邊界元模擬[J].地震工程與工程振動(dòng),2000,20(2):51-56.

[6]包光偉,王振強(qiáng),張?zhí)煜?等.火箭推進(jìn)劑液體晃動(dòng)關(guān)機(jī)響應(yīng)的數(shù)值仿真[J].宇航學(xué)報(bào),2002,23(2):84-88.

[7]周宏,李俊峰,王天舒.用ALE有限元模擬的網(wǎng)格更新方法[J].力學(xué)學(xué)報(bào),2008,40(2):267-272.

[8]尚春雨,趙金城.用FLUENT分析剛性容器內(nèi)液面晃動(dòng)問(wèn)題[J].上海交通大學(xué)學(xué)報(bào),2008,42(6):953-956.

[9]李青,馬興瑞,王天舒.非軸對(duì)稱貯箱液體晃動(dòng)的等效力學(xué)模型[J].宇航學(xué)報(bào),2011,32(2):242-249.

[10]LIU Dongming,LIN Pengzhi.A numerical study of three-dimensional liquid sloshing in tanks[J]. Journal of Computational Physics,2008,227: 3921-3939.

[11]趙玉成，張亞紅，白長(zhǎng)青，等.固體火箭發(fā)動(dòng)機(jī)模態(tài)分析的縮聚方法[J].固體火箭技術(shù),2004，27(2)：98-100.

[12]朱安文，曲廣吉，高耀南.航天器結(jié)構(gòu)動(dòng)力模型修正中的縮聚方法[J]. 中國(guó)空間科學(xué)技術(shù)，2003(2)：6-10.

[13]梅強(qiáng)中.水波動(dòng)力學(xué)[M].北京：科學(xué)出版社，1984.

[編輯] 李啟棟

10.3969/j.issn.1673-1409(N).2012.11.035

TE972 107

A

16731409(2012)11N10703