有關(guān)初中數(shù)學多面體的一些規(guī)律探索

周秀麗

（濰坊市北海雙語學校，山東 濰坊 261200）

我們生活的空間是三維空間，人們在生活、生產(chǎn)中所直接接觸的是各種各樣的物體，所以對物體的形狀、大小和數(shù)學性質(zhì)進行研究，可以幫助學生進一步豐富對空間圖形的認識和了解，理解二維與三維圖形之間的聯(lián)系，培養(yǎng)學生的應用意識。

初中數(shù)學課程標準對“空間與圖形”的總體目標做了如下描述：豐富學生對現(xiàn)實空間及圖形的認識，建立初步的空間觀念，發(fā)展學生形象思維，發(fā)展幾何直覺。“空間與圖形”的內(nèi)容主要涉及現(xiàn)實世界中的物體、幾何體和平面圖形的形狀、大小、位置關(guān)系及其變換，它是人們更好地認識和描述生活空間并進行交流的重要工具。

空間觀念的形成不像拍照，要想建立空間觀念，必須有觀察、操作、想象、思考、推理、驗證等一系列過程。這個過程，不僅是一個實踐的過程，更是一個探索的過程，一個循序漸進的過程。下面以“多面體”的相關(guān)知識為例，探索其所蘊含的某些規(guī)律，以便于幫助學生更好地認識和理解生活的空間，培養(yǎng)學生的創(chuàng)新精神。

一、多面體的頂點數(shù)、面數(shù)、棱數(shù)

（一）棱柱

觀察圖1，填寫下表，你發(fā)現(xiàn)了什么規(guī)律？

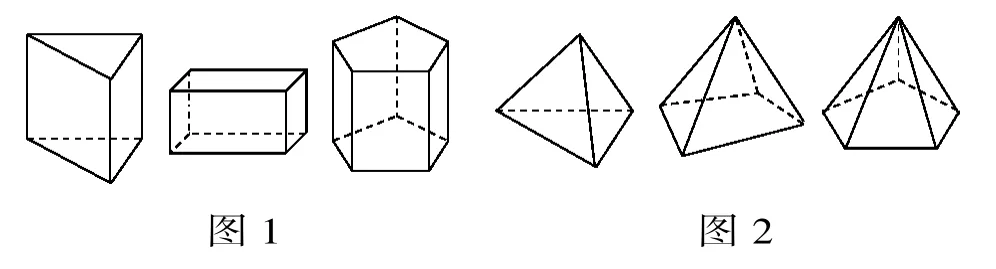
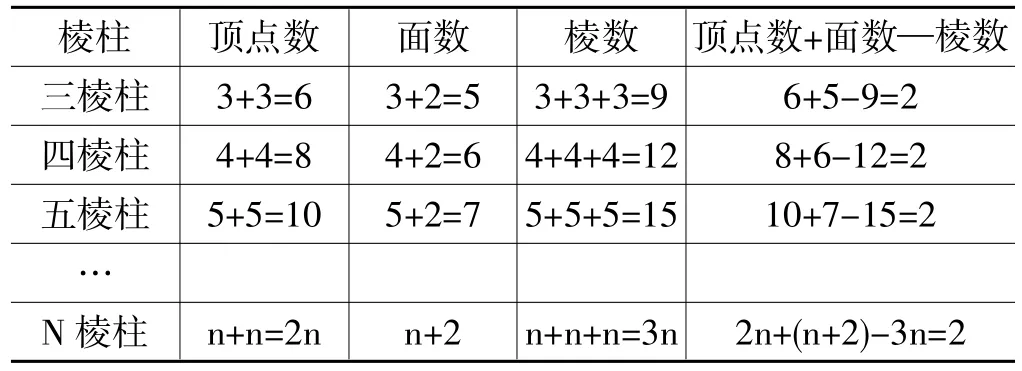
棱柱 頂點數(shù) 面數(shù) 棱數(shù) 頂點數(shù)+面數(shù)—棱數(shù)三棱柱 3+3=6 3+2=5 3+3+3=9 6+5-9=2四棱柱 4+4=8 4+2=6 4+4+4=12 8+6-12=2五棱柱 5+5=10 5+2=7 5+5+5=15 10+7-15=2…N棱柱 n+n=2n n+2 n+n+n=3n 2n+(n+2)-3n=2

總結(jié)：N棱柱有2n個頂點，n+2個面，3n條棱，頂點數(shù)+面數(shù)—棱數(shù)=2.

練習：1.一個棱柱有18條棱，那么它的底面一定是（ ）

A.十八邊形 B.八邊形 C.六邊形 D.四邊形

2.一個直棱柱有12個頂點，那么它的面的個數(shù)是（ ）

A.10個 B.9個 C.8個 D.7個

3.下列結(jié)論中，錯誤的是（ ）

A.棱柱的側(cè)面數(shù)與側(cè)棱數(shù)相同

B.棱柱的棱數(shù)一定是3的倍數(shù)

C.棱柱的頂點數(shù)一定是偶數(shù)

D.棱柱的面數(shù)一定是奇數(shù)

答案：1.C 2.C 3.D

（二）棱錐

觀察圖2，填寫下表，你發(fā)現(xiàn)了什么規(guī)律？

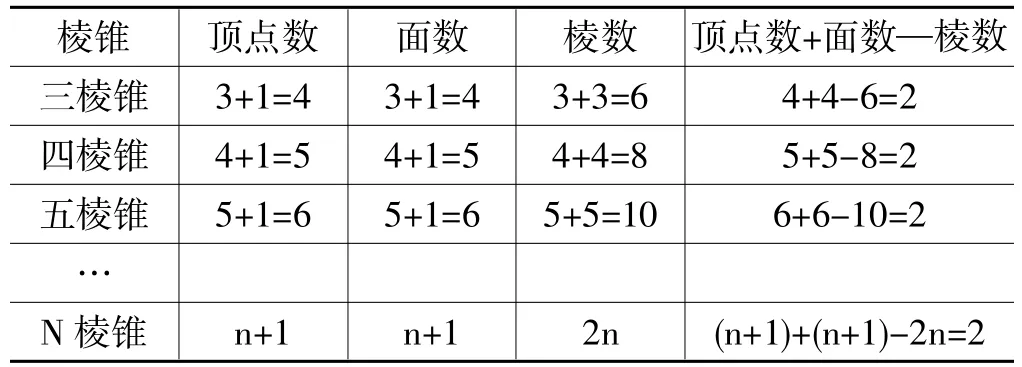
棱錐 頂點數(shù) 面數(shù) 棱數(shù) 頂點數(shù)+面數(shù)—棱數(shù)三棱錐 3+1=4 3+1=4 3+3=6 4+4-6=2四棱錐 4+1=5 4+1=5 4+4=8 5+5-8=2五棱錐 5+1=6 5+1=6 5+5=10 6+6-10=2…N棱錐 n+1 n+1 2n (n+1)+(n+1)-2n=2

總結(jié)：N 棱錐有(n+1)個頂點，(n+1)個面，2n條棱，頂點數(shù)+面數(shù)—棱數(shù)=2.

練習：1.正四面體的頂點數(shù)和棱數(shù)分別是（ ）

A.3，4 B.3，6 C.4，4 D.4，6

2.（1）三棱錐有6條棱，4個面，四棱錐有_____條棱，_____個面；

（2）_____棱錐有30條棱；

（3）有沒有一個多棱錐，其棱數(shù)是2006，若有，求出有多少個面；若沒有，說明理由.

答案：1.D2.（1）8，5；（2）15；（3）有，1004個面.

歸納：簡單多面體的頂點數(shù)V、棱數(shù)E及面數(shù)F間的關(guān)系式V+F-E=2叫做歐拉公式。

練習：（2010·寧波）十八世紀瑞士數(shù)學家歐拉證明了簡單多面體中頂點數(shù)（V）、面數(shù)（F）、棱數(shù)（E）之間存在的一個有趣的關(guān)系式，被稱為歐拉公式.請你觀察圖3下列幾種簡單多面體模型，解答下列問題：

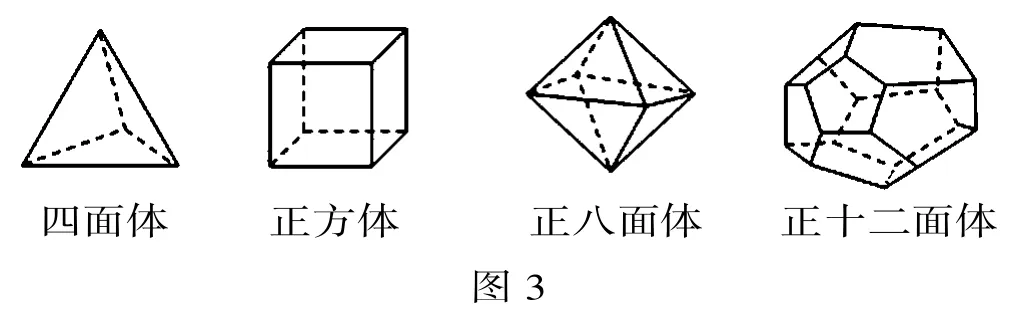
（1）根據(jù)上面的多面體模型，完成表格中的空格：

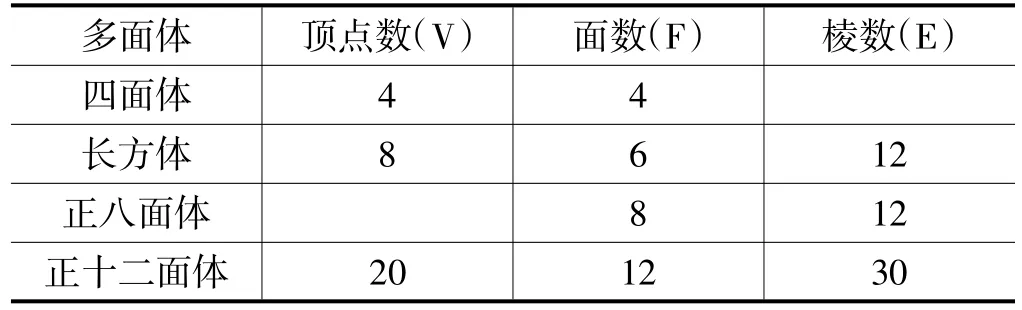
多面體 頂點數(shù)（V） 面數(shù)（F） 棱數(shù)（E）四面體 4 4長方體 8 6 12正八面體 8 12正十二面體 20 12 30

你發(fā)現(xiàn)頂點數(shù)（V）、面數(shù)（F）、棱數(shù)（E）之間存在的關(guān)系式是________.

（2）一個多面體的面數(shù)比頂點數(shù)大8，且有30條棱，則這個多面體的面數(shù)是________.

（3）某個玻璃制品的外形是簡單多面體，它的外表面是由三角形和八邊形兩種多邊形拼接而成，且有24個頂點，每個頂點處都有3條棱，設(shè)該多面體外表三角形的個數(shù)為x個，八邊形的個數(shù)為y個，求x+y的值.

答案：（1）6，6；V+F-E=2.（2）20.（3）這個多面體的面數(shù)為x+y，棱數(shù)為條，根據(jù) V+F-E=2，可得24+（x+y）-36=2，所以 x+y=14.

二、多面體的表面展開圖，需要剪斷的棱數(shù)

（一）棱柱

把一個N棱柱沿著某些棱剪斷展開成平面圖形，需要剪幾刀？

探索

1.三棱柱

（1）動手操作，將一個三棱柱沿著某些棱剪開，展成平面圖形，需要剪幾刀？

（2）觀察如圖4所示的三棱柱的表面展開圖，需要剪幾刀，才能展成平面圖形？

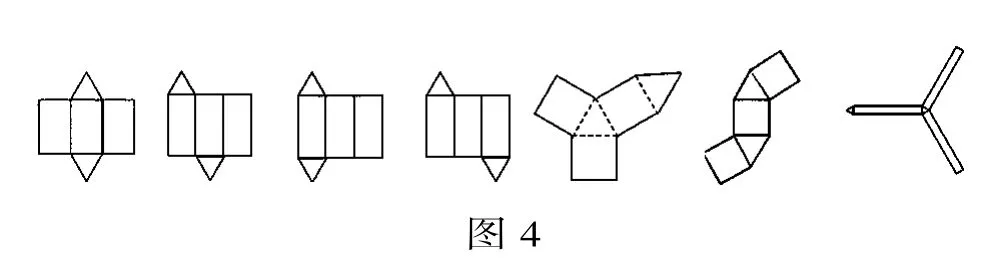
分析：圖4中的前四幅圖，都可以看成是剪斷1條側(cè)棱和4條（上下各2條）底棱得到的；后三幅圖，都可以看成是剪斷3條側(cè)棱和2條底棱得到的.三棱柱共有9條棱，其中各展開圖中均有4條棱是連在一起的，5條棱斷開了.共需要剪5刀.

2.四棱柱

如圖5，要將一個正方體模型剪開成平面圖形，需要剪斷多少條棱？

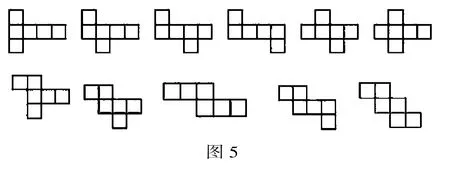
分析：圖5中的前6幅圖，都可以看成是剪斷1條側(cè)棱和6條（上下各3條）底棱得到的；后5幅圖可看作是剪斷2條側(cè)棱和5條底棱、3條側(cè)棱和4條底棱而得到的.四棱柱共有12條棱，其中各展開圖中均有5條棱是連在一起的，7條棱斷開了.共需要剪7刀.

3.五棱柱、六棱柱

如圖6，要將一個五棱柱六棱柱展開成平面圖形，分別需要剪斷多少條棱？

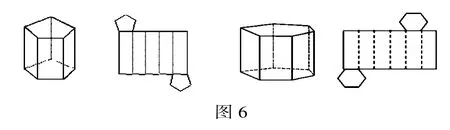
分析：從圖6中可以看出，五棱柱和六棱柱的表面展開圖，都是剪斷了1條側(cè)棱，然后再分別剪斷8條（上下各2條）、10條（上下各2條）底棱而得到的。五棱柱共有15條棱，展開圖中6條棱是連在一起的，9條棱斷開了，共需要剪9刀；六棱柱共有18條棱，展開圖中有7條棱是連在一起的，11條棱斷開了，共需要剪11刀.

總結(jié)：如下表，要將一個N棱柱展開成平面圖形，需要剪斷（2n-1）條棱.

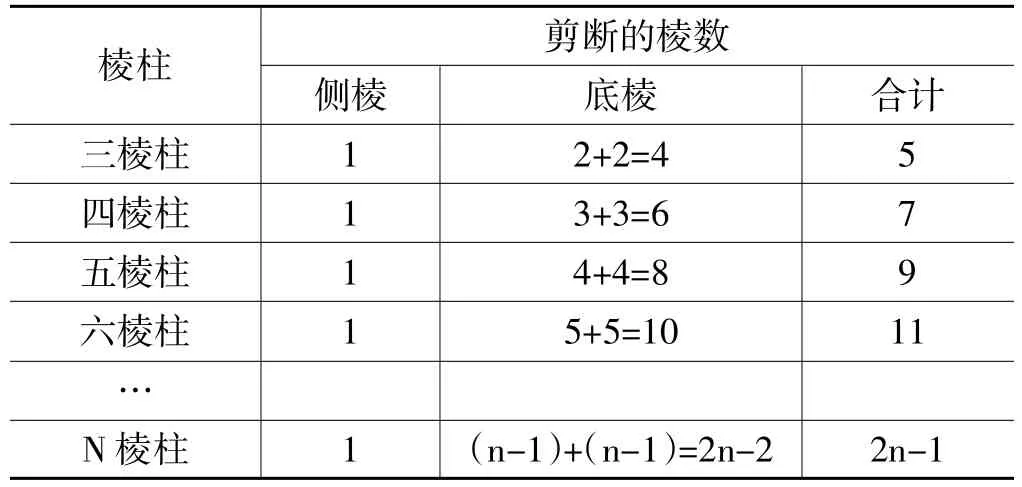
棱柱 剪斷的棱數(shù)側(cè)棱 底棱 合計三棱柱 1 2+2=4 5四棱柱 1 3+3=6 7五棱柱 1 4+4=8 9六棱柱 1 5+5=10 11…N棱柱 1 （n-1）+（n-1）=2n-2 2n-1

（二）棱錐

把一個N棱錐沿著某些棱展開成平面圖形，需要剪幾刀？

1.三棱錐

（1）動手操作，將一個三棱柱沿著某些棱剪開，展成平面圖形，需要剪幾刀？

（2）觀察如圖7所示的三棱柱的表面展開圖，需要剪幾刀，才能展成平面圖形？

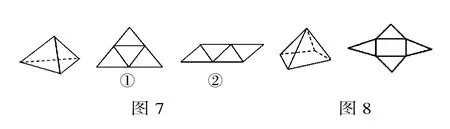
分析：把四面體的底面固定不動，沿三條側(cè)棱剪開，展在平面上，即得①，把四面體的底面和相鄰的一個側(cè)面的棱不剪，其余的棱剪開，展開在一個平面上，得到②.可以剪斷3條側(cè)棱；或2條側(cè)棱，1條底棱；或1條側(cè)棱，2條底棱；或3條底棱，有3條棱連在一起，3條棱斷開.共需要剪3刀.

2.四棱錐

如圖8，要將一個四棱錐正方體模型剪開成平面圖形，需要剪斷多少條棱？

分析：可以剪斷4條側(cè)棱，也可以剪斷4條底棱，或者采用其他的方法.共需要剪4刀.

3.五棱錐

如圖9，要將一個五棱錐正方體模型剪開成平面圖形，需要剪斷多少條棱？

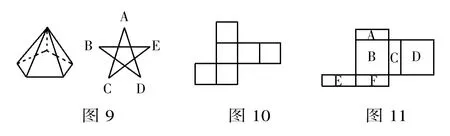
分析：仿照四棱錐的剪斷方法，可以剪斷5條側(cè)棱，也可以剪斷5條底棱.共需要剪5刀.

練習：要將一個N棱錐展開成平面圖形，需要剪斷多少條棱？

總結(jié)：通過以上三棱錐、四棱錐、五棱錐的探究，要將一個N棱錐展開成平面圖形，需要剪斷n條棱.

三、利用實物模型，實現(xiàn)由平面到立體的轉(zhuǎn)換

學生的空間知識來自豐富的現(xiàn)實原型，與現(xiàn)實生活關(guān)系非常緊密，這是他們理解和發(fā)展空間觀念的寶貴資源，教學過程中要引導他們充分利用身邊的實物模型.

如圖10是一個多面體展開圖，每個面內(nèi)都標注了字母，請根據(jù)要求回答問題：

（1）如果面A在多面體的底部，那么在上面的一面是_____；

（2）如果面F在前面，從左面看面B，那么在上面的一面是_____；

（3）從右面看是面C，面D在后面，那么在上面的一面是_____.

分析：這是一個正方體的表面展開圖，要變成一個空間圖形，需從相對面入手，分析及解答問題.共有六個面，其中面“A”與面“F”相對，面“B”與面“D”相對，“C”與面“E”相對.也可利用身邊的立方體（或長方體）模型，如手中的橡皮、文具盒、課本等實物，根據(jù)題意在各個面上標上字母，再動手操作.

解：（1）由圖可知，面“A”與面“F”相對，∴ 面 A 在多面體的底部，那么在上面的一面是F；

（2）由圖可知，如果F面在前面，B面在左面，那么“E”面在下面，∵ 面“C”與面“E”相對，∴ 在上面的一面是C；

（3）由圖可知，如果C面在右面，D面在后面，那么“F”面在下面，∵ 面“A”與面“F”相對，∴ 在上面的一面是 A.故答案為：F，C，A.

總結(jié)：實現(xiàn)由表面展開圖到立體圖形的轉(zhuǎn)化，可借助實物模型，既可以向“外”折，也可以向“里”折.但要保證所標字母或圖案露在外面，必須向“里”折.

練習：如圖11，一個正方體共有12條棱，展開圖中連在一起的有5條，所以要剪7條，如圖所示，是一個多面體展開圖，每個面都標注了字母，請回答：如果A在前面，從左面看是D，那么其他各面分別在什么位置？

答案：上面是C，下面是E，右面是B，后面是F.